
Задачи с решениями
-
Найти площадь части сферы
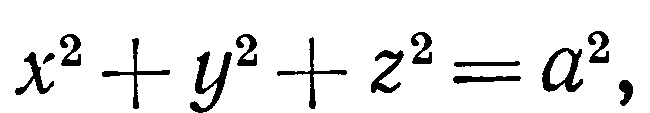
заключенной внутри цилиндра
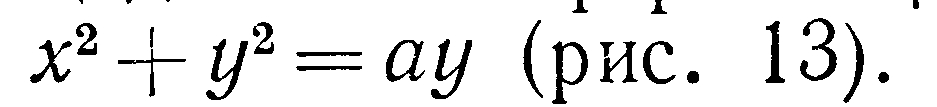
Решение Из уравнения сферы имеем
(для I октанта):
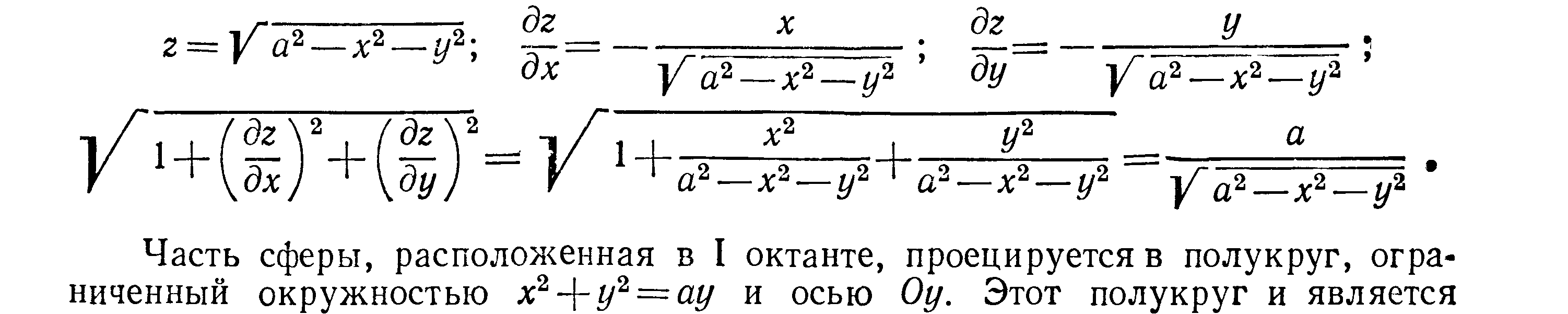
областью интегрирования D.
Поверхность расположена в четырех
октантах потому искомая площадь
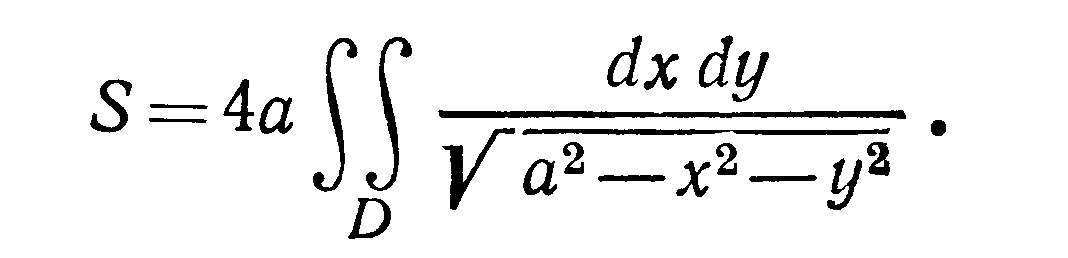
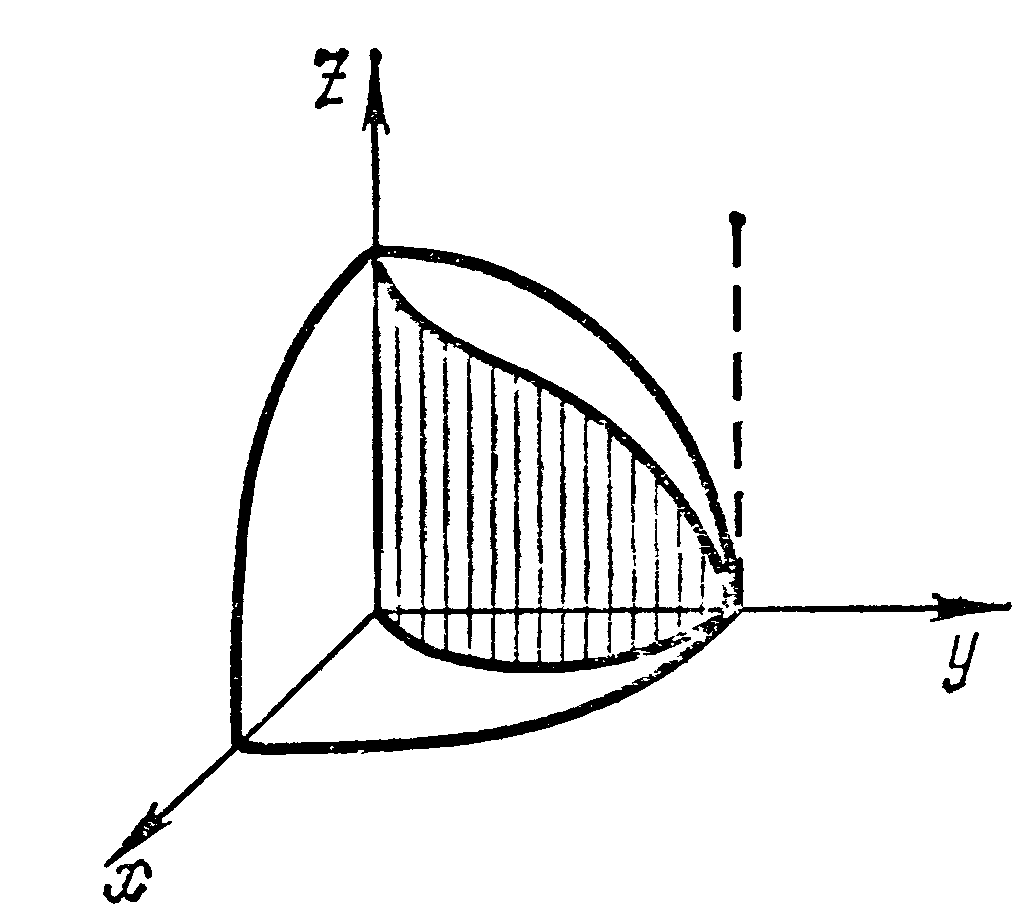
Перейдем к полярным координатам, тогда
уравнение окружности примет вид
![]()
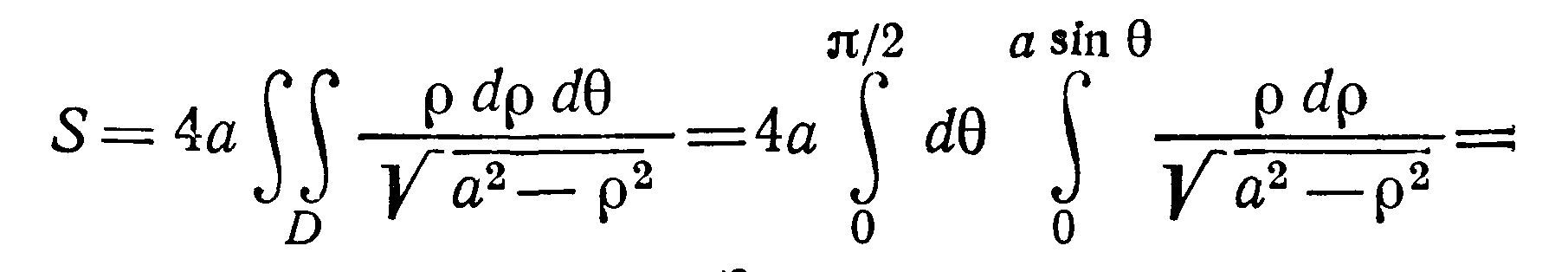
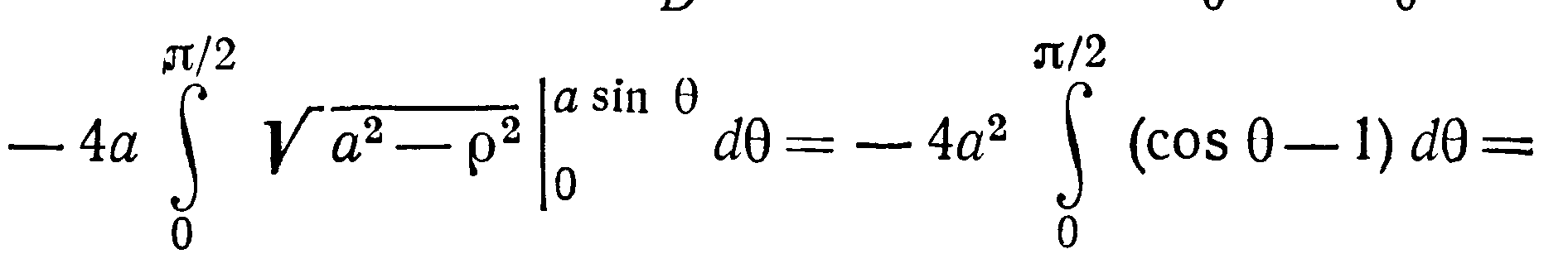
![]()
-
Найти площадь части конуса
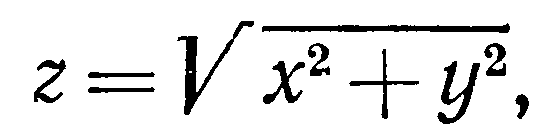
внутри цилиндра
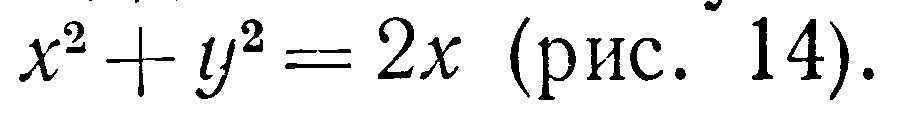
Решение Из уравнения конуса
имеем
![]()
Областью
интегрирования D является круг,
ограниченный окружностью
![]()
![]()
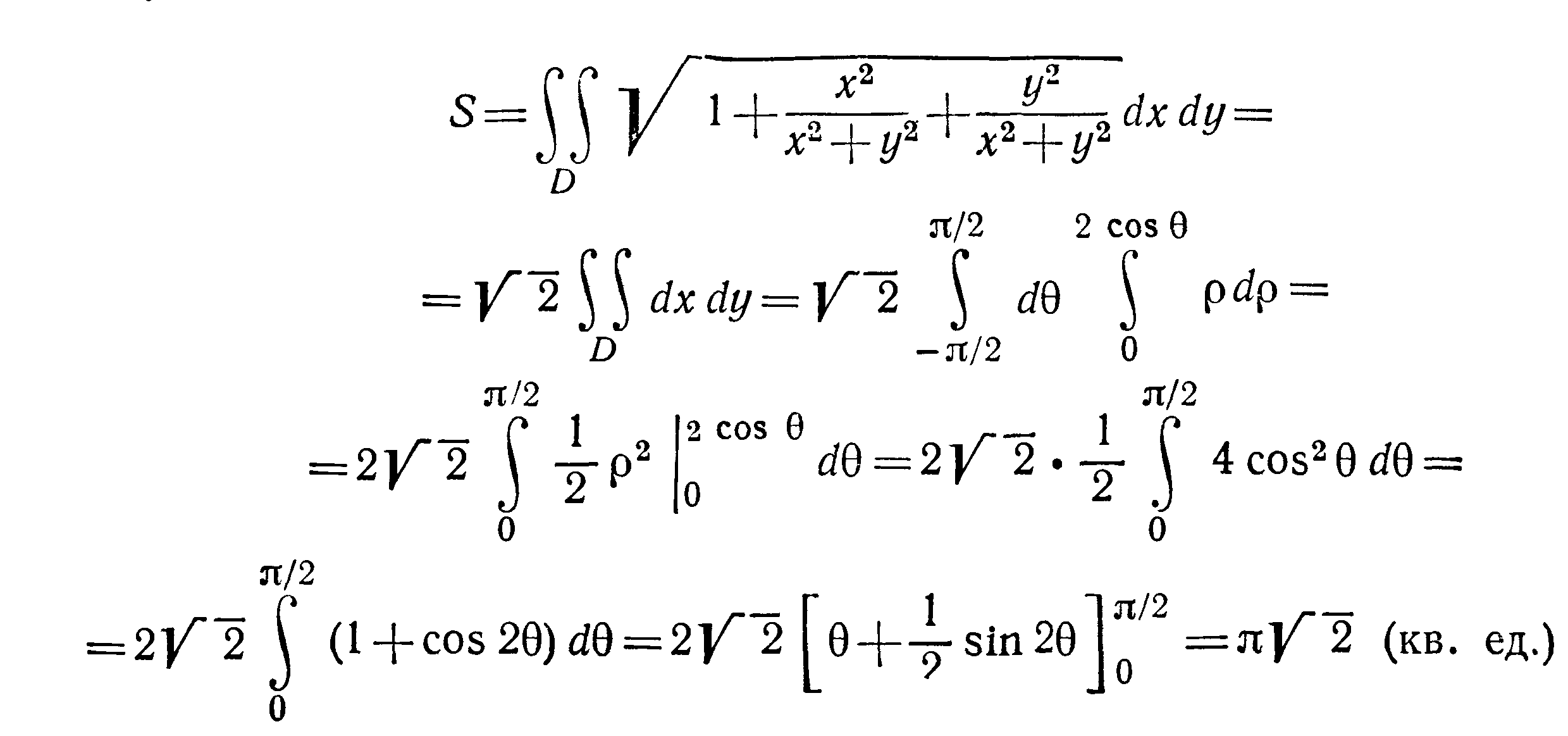
-
Вычислить площадь поверхности цилиндра
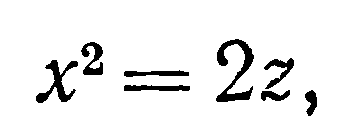
отсеченной плоскостями
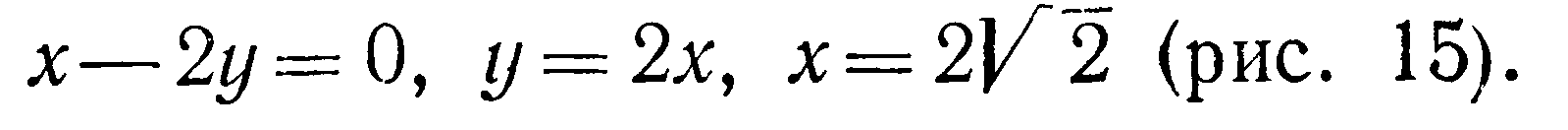
Решение Областью интегрирования
служит треугольник ОАВ. Из уравнения
цилиндра имеем
![]()
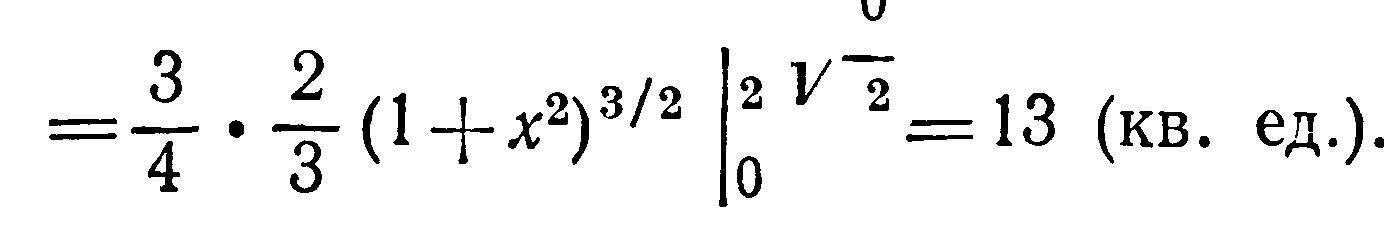
-
Вычислить площадь части поверхности
параболоида x
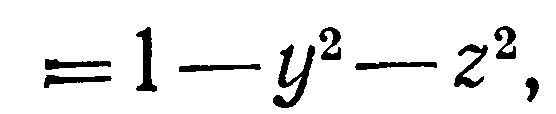
,
вырезанной цилиндром
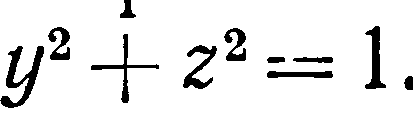
Решение Область интегрирования
– окружность
![]()
(она расположена в плоскости yOz).
Из уравнения параболоида имеем
![]()
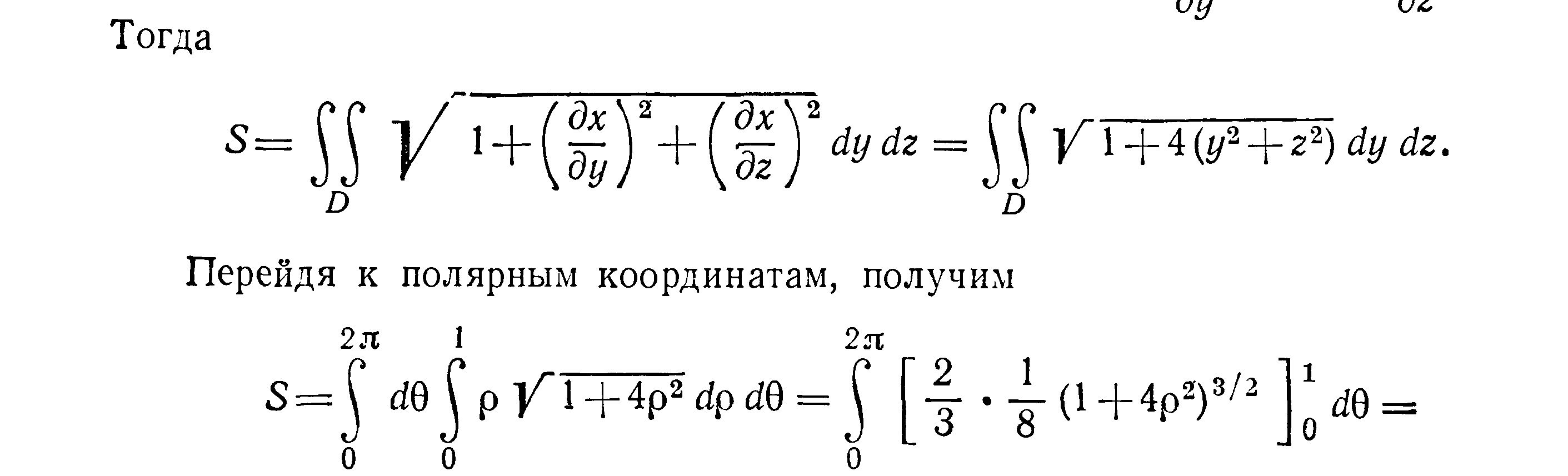
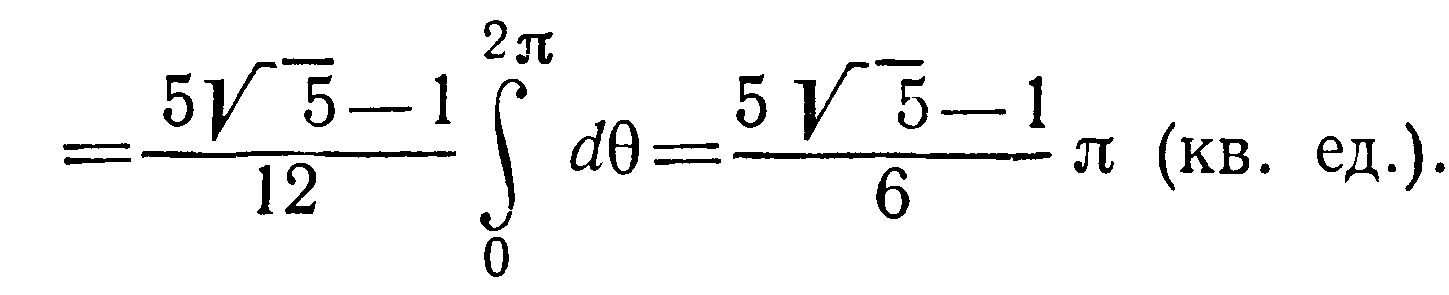
Задачи
36 . Найти площадь части поверхности
![]()
вырезанной цилиндром
![]()
37. Найти площадь части сферы
![]()
вырезанной цилиндром
![]()
38. Найти площадь той части плоскости z=
x:, которая заключена
внутри цилиндра
![]()
39. Найти площадь части поверхности
цилиндра z = x2,
вырезанной плоскостями
![]()
40. Вычислить площадь поверхности конуса
![]()
расположенной внутри цилиндра
![]()
41. Вычислить площадь поверхности цилиндра
![]()
расположенной внутри цилиндра
![]()
42. Найти площадь части поверхности
![]()
вырезанной плоскостями
![]()
Индивидуальные задания
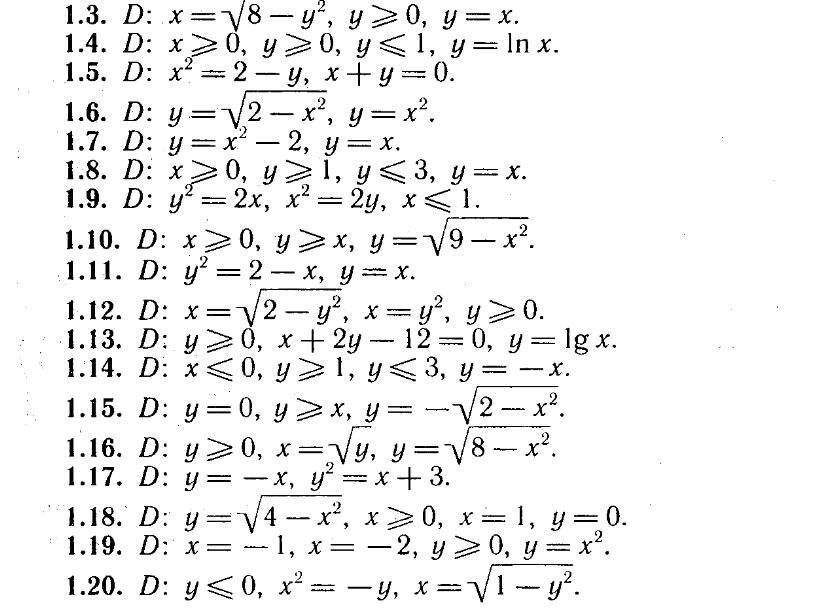
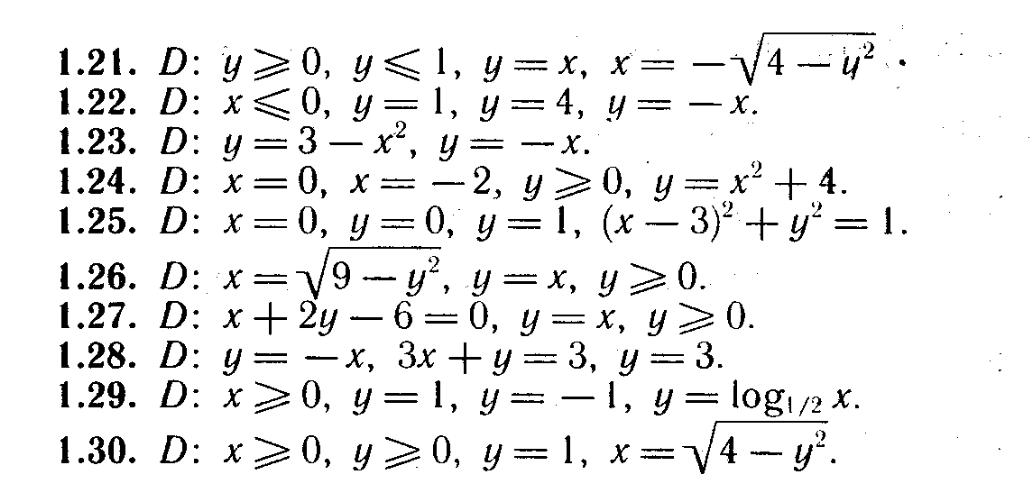
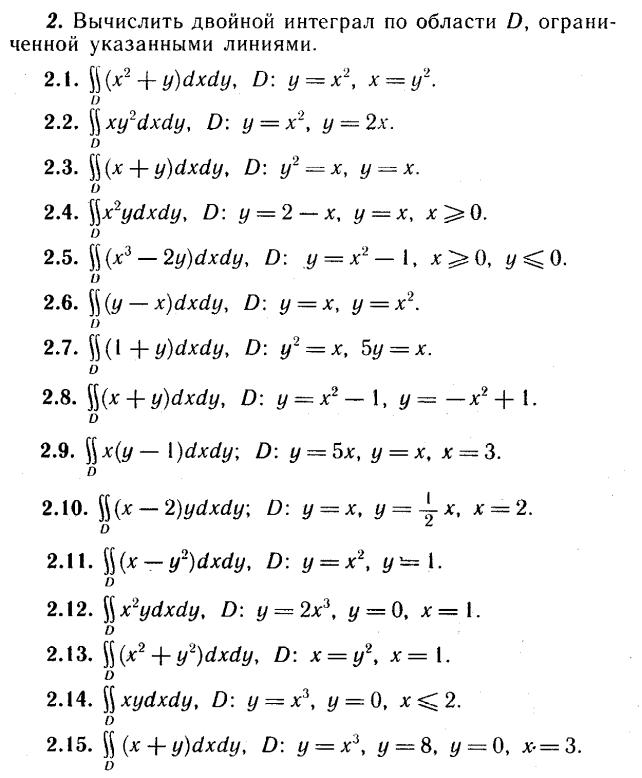
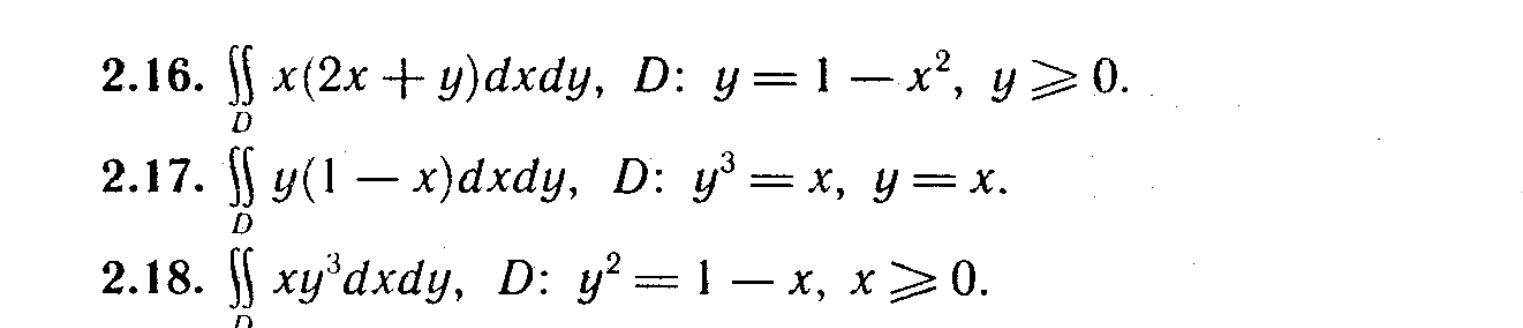

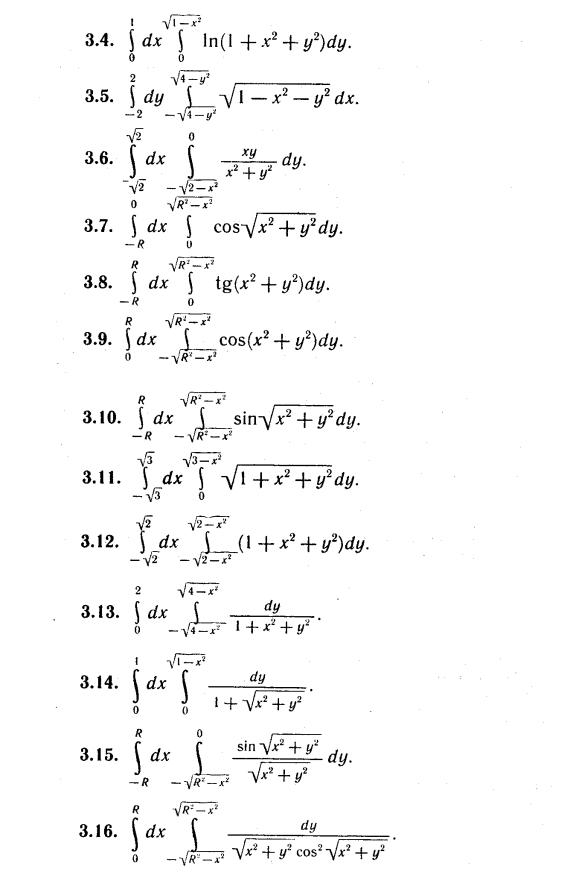




Тройной интеграл
Пусть функция f (х, у, z)
определена в ограниченной замкнутой
пространственной области Т. Разобьем
область Т произвольным образом на п
элементарных областей T1
Т2, …, Тn с
диаметрами d1 d2,
…, dn и объемами ∆V1,
∆V2, ….,∆Vn.
В каждой элементарной области возьмем
произвольную точку Pk
(ξ1, ξ2, … , ξn
) и умножим значение функции в точке Рk
на объем этой области.
Интегральной суммой для функции f
(х, у, z) по области Т
называется сумма вида
![]()
Предел интегральной суммы при стремлении
к нулю наибольшего из диаметров всех
элементарных областей ∆Vk
называется тройным интегралом от функции
f (х, у, z) по
области Т и обозначается следующим
образом:
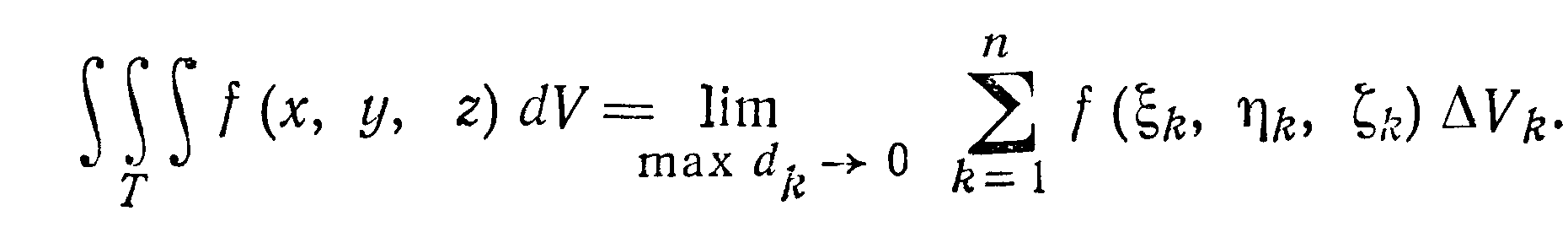
Конечный предел такого вида может
существовать только для ограниченной
функции.
Если f (х, у, z)
> 0 в области Т, то тройной интеграл
![]()
представляет собой массу тела, занимающего
область Т и имеющего переменную плотность
γ = f(x, у, z)
(физическое истолкование тройного
интеграла).
Основные свойства тройных интегралов
аналогичны свойствам двойных интегралов.
В декартовых координатах тройной
интеграл обычно записывают в виде
![]()
Пусть область интегрирования Т
определяется неравенствами x1≤
x≤ x2, y1≤
y ≤ y2,
z1≤ z
≤ z2, где y1(x),
y2(x),
z1(x,y),
z2 (x,y)
непрерывные функции. Тогда тройной
интеграл от функции f (х,
у, z), распространенный на область Т,
вычисляется по формуле
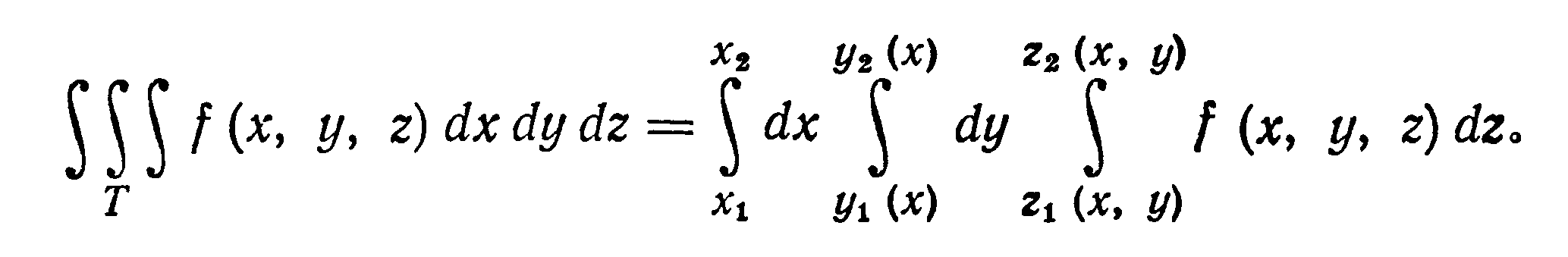
Если при вычислении тройного интеграла
требуется перейти от переменных х, у, z
к новым переменным и, v, w, связанным с х,
у, z соотношениями х = х(u,
v, w), y = y(u, v, w), z = z (u, v, w), где
функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные
вместе со своими частными производными
первого порядка, устанавливают взаимно
однозначное и в обе стороны непрерывное
соответствие между точками области Т
пространства Oxyz и точками некоторой
области Т’ пространства Ouvw и якобиан J
в области Т’ не обращается в нуль
то пользуются формулой
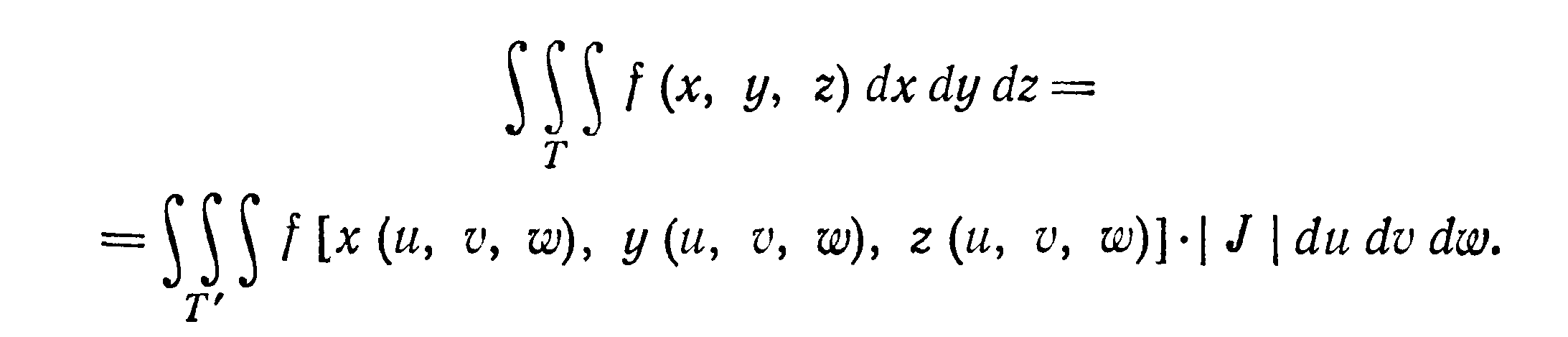
В частности, при переходе от декартовых
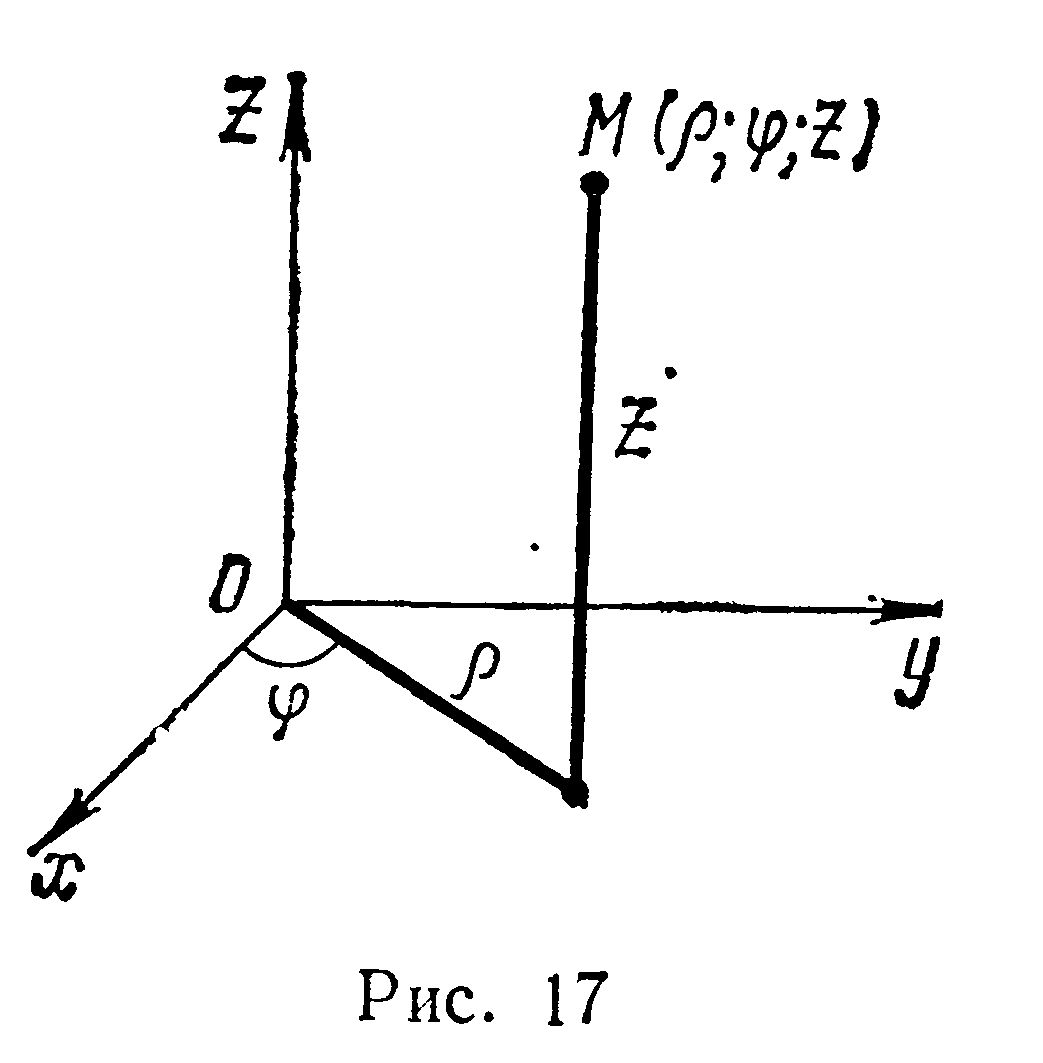
координат х, у, z к
цилиндрическим координатам ρ,φ , z
(рис. 17), связанным с х, у, z
соотношениями
![]()
якобиан преобразования J = ρ
и формула преобразования тройного
интеграла
к цилиндрическим координатам имеет вид
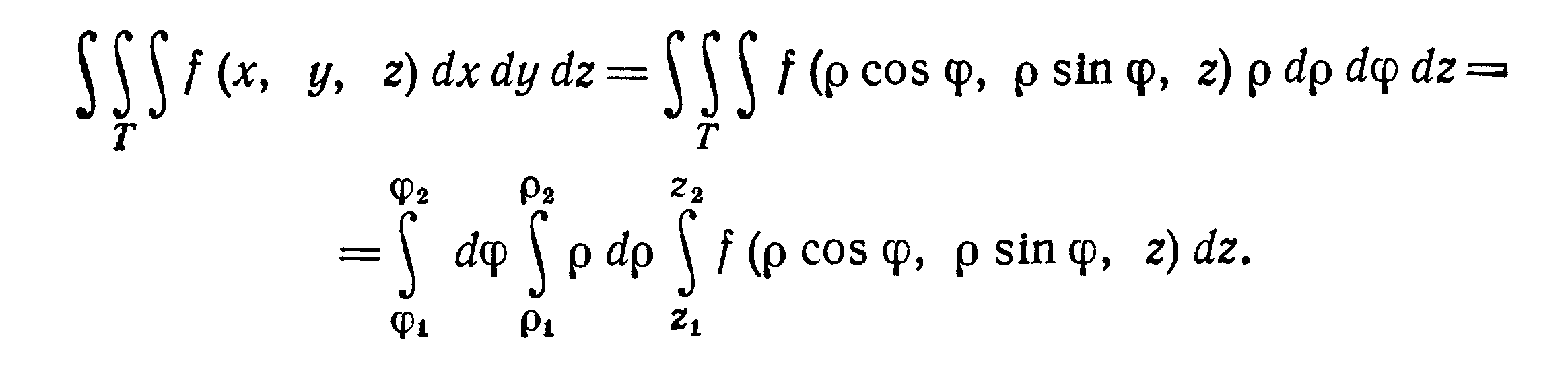
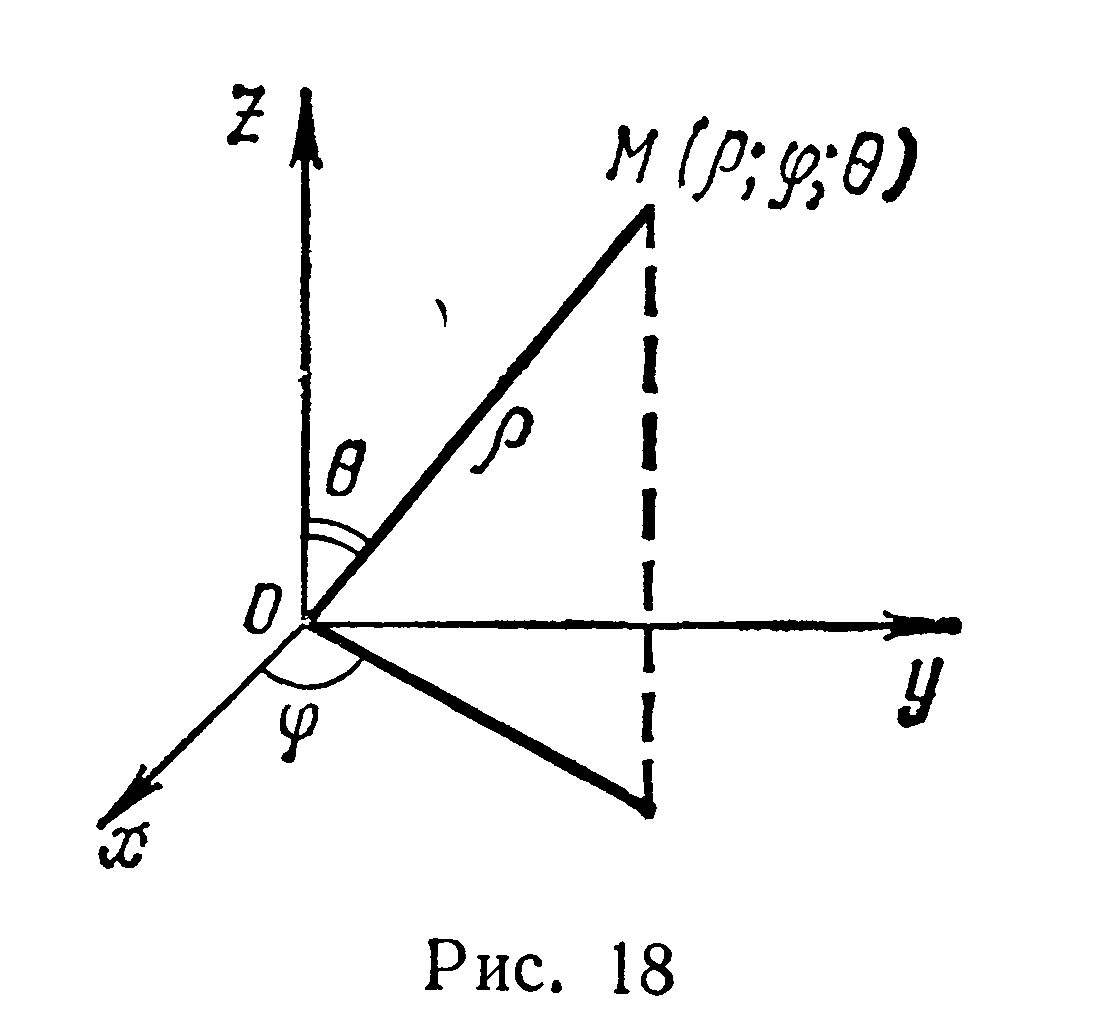
При переходе от декартовых координат
х, у, z к сферическим координатам ρ,φ,θ
(рис. 18), связанным с х, у, z соотношениями
![]()
![]()
якобиан преобразования J
= ρ2 sinθ, и формула
преобразования тройного интеграла к
сферическим координатам имеет вид
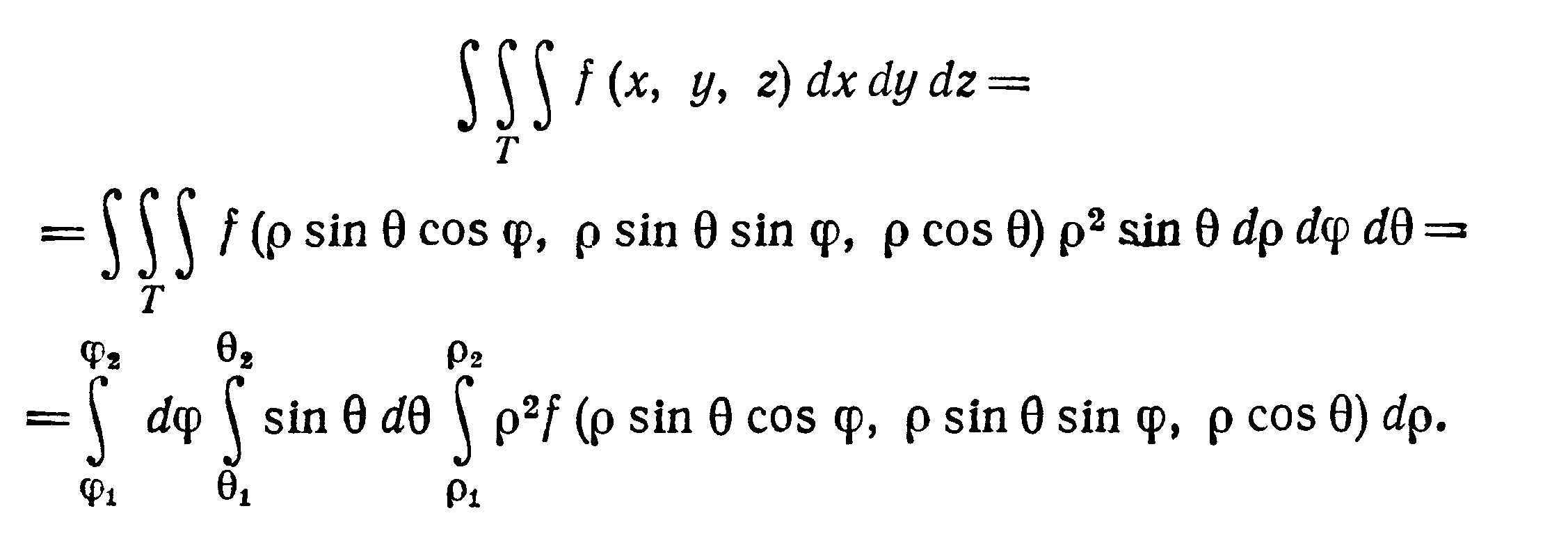
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление площади поверхности
Пример 1
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой
$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $
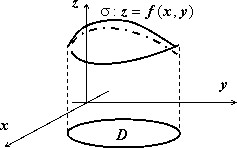
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .
Решение:
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.
Область $mathbf { textit { D } } $ – сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:
$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.
Пример 2
Вычислить площадь cферы радиуса (a.)
Решение:
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } – { x^2 } – { y^2 } } . } $
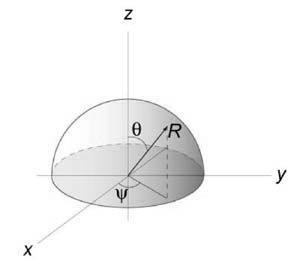
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$
Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } x } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } y } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { y } { z } . } $
Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $
Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } – { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aintlimits_0^a { frac { { dleft( { { a^2 } – { r^2 } }right) } } { { 2sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aleft. { left( { sqrt { { a^2 } – { r^2 } } }right) }right|_ { r = 0 } ^a } = { – 2pi aleft( { 0 – a }right) = 2pi { a^2 } . } $
Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$
Макеты страниц
(см. § 6, гл. IX, т. I). На этой плоскости выделим такую площадку  которая проектируется на плоскость Оху в виде площадки
которая проектируется на плоскость Оху в виде площадки  . Рассмотрим сумму всех площадок
. Рассмотрим сумму всех площадок 
Предел а этой суммы, когда наибольший из диаметров площадок  стремится к нулю, мы будем называть площадью поверхности, т. е. по определению положим
стремится к нулю, мы будем называть площадью поверхности, т. е. по определению положим

Займемся теперь вычислением площади поверхности. Обозначим через  угол между касательной плоскостью и плоскостью Оху.
угол между касательной плоскостью и плоскостью Оху.

Рис. 323.

Рис. 324.
На основании известной формулы аналитической геометрии можно написать (рис. 324)

или

Угол  – есть в то же время угол между осью
– есть в то же время угол между осью  и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем
и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем

Следовательно,

Подставляя это выражение в формулу (2), получим

Так как предел интегральной суммы, стоящей в правой части последнего равенства, по определению представляет собой двойной интеграл  то окончательно получаем
то окончательно получаем

Это и есть формула, по которой вычисляется площадь поверхности 
Если уравнение поверхности дано в виде  или в виде
или в виде  , то соответствующие формулы для вычисления поверхности имеют вид
, то соответствующие формулы для вычисления поверхности имеют вид

где  – области на плоскостях
– области на плоскостях  в которые проектируется данная поверхность.
в которые проектируется данная поверхность.
Пример 1. Вычислить поверхность а сферы

Решение. Вычислим поверхность верхней половины сферы  . В этом случае
. В этом случае

Следовательно, подынтегральная функция примет вид

Область интегрирования определяется условием  . Таким образом, на основании формулы (4) будем иметь
. Таким образом, на основании формулы (4) будем иметь

Для вычисления полученного двойного интеграла перейдем к полярным координатам. В полярных координатах граница области интегрирования
определяется уравнением  . Следовательно,
. Следовательно,

Пример 2. Найти площадь той части поверхности цилиндра  которая вырезается цилиндром
которая вырезается цилиндром 

Рис. 325.

Рис. 326.
Решение. На рис. 326 изображена  часть искомой поверхности. Уравнение поверхности имеет вид
часть искомой поверхности. Уравнение поверхности имеет вид  ; поэтому
; поэтому 

Область интегрирования представляет собой четверть круга, т. е. определяется условиями

Следовательно,

§ 8. Плотность распределения вещества и двойной интеграл
Пусть в области D распределено некоторое вещество, так что на каждую единицу площади области D приходится определенное количество этого вещества. Мы будем говорить в дальнейшем о распределении массы, хотя наши рассуждения сохранятся и в том случае, когда идет речь о распределении электрического заряда, количества тепла и т. п.
Рассмотрим произвольную площадку  области D. Пусть масса вещества, приходящаяся на данную площадку, есть
области D. Пусть масса вещества, приходящаяся на данную площадку, есть 
Тогда отношение  называется средней поверхностной плотностью вещества в области
называется средней поверхностной плотностью вещества в области  .
.
Пусть теперь площадка  уменьшается, стягиваясь к точке
уменьшается, стягиваясь к точке  . Рассмотрим предел
. Рассмотрим предел  Если этот предел существует, то, вообще говоря, он будет зависеть от положения точки Р, т. е. от ее координат х и у, и будет представлять собой некоторую функцию
Если этот предел существует, то, вообще говоря, он будет зависеть от положения точки Р, т. е. от ее координат х и у, и будет представлять собой некоторую функцию  точки Р. Будем называть этот предел поверхностной плотностью вещества в точке Р:
точки Р. Будем называть этот предел поверхностной плотностью вещества в точке Р:

Таким образом, поверхностная плотность есть функция  координат точки области.
координат точки области.
Пусть теперь, обратно, в области D задана поверхностная плотность некоторого вещества как некоторая непрерывная функция  и требуется определить общее количество вещества М, содержащегося в области D. Разобьем область D на площадки
и требуется определить общее количество вещества М, содержащегося в области D. Разобьем область D на площадки  и в каждой площадке возьмем точку
и в каждой площадке возьмем точку  тогда
тогда  есть поверхностная плотность в точке
есть поверхностная плотность в точке 
Произведение  с точностью до бесконечно малых высшего порядка, дает нам количество вещества, содержащегося на площадке
с точностью до бесконечно малых высшего порядка, дает нам количество вещества, содержащегося на площадке  а сумма
а сумма  приближенно выражает общее количество вещества, распределенного в области D. Но это — интегральная сумма для функции
приближенно выражает общее количество вещества, распределенного в области D. Но это — интегральная сумма для функции  в области D. Точное значение мы получим в пределе при
в области D. Точное значение мы получим в пределе при 
Таким образом,

т. e. общее количество вещества в области D равно двойному интегралу по области D от плотности  этого вещества.
этого вещества.
Пример. Определить массу круглой пластинки радиуса  если поверхностная плотность
если поверхностная плотность  материала пластинки в каждой точке
материала пластинки в каждой точке  пропорциональна расстоянию точки
пропорциональна расстоянию точки  от центра круга, т. е. если
от центра круга, т. е. если

Решение. По формуле (2) имеем

где область интегрирования D есть круг 
Переходя к полярным координатам, получаем 

Случай явного задания поверхности. Площадь Гладкой поверхности
Гладкой поверхности  Выражается формулой
Выражается формулой
 (19.19)
(19.19)
Где – проекция данной поверхности на плоскость
– проекция данной поверхности на плоскость
Если поверхность имеет уравнение вида То
То
 (19.20)
(19.20)
Где — проекция поверхности на ось
— проекция поверхности на ось
Если поверхность задана уравнением, , то
, то
 (19.21)
(19.21)
Где — проекция поверхности на ось
— проекция поверхности на ось
Случай неявного задания поверхности. Площадь Поверхности, заданной уравнением
Поверхности, заданной уравнением Выражается интегралом
Выражается интегралом
 (19.22)
(19.22)
Где – проекция поверхности на плоскость
– проекция поверхности на плоскость
Случай параметрического задания поверхности. Если поверхность задана параметрическими уравнениями
Где – ограниченная замкнутая квадрируемая область, в которой
– ограниченная замкнутая квадрируемая область, в которой
Функции х, у, z непрерывно дифференцируемы, то

(19.24)
Где
 (19.25)
(19.25)
Пример 19.17. Найти площадь части поверхности цилиндра  Заключенной внутри сферы
Заключенной внутри сферы (боковая поверх
(боковая поверх
Ность «тела Вивиани», рис. 19.19).
Применим формулу (19.20). Поскольку плоскостью Цилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности. Вычислим площадь той части поверхности, уравнение которой
Цилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности. Вычислим площадь той части поверхности, уравнение которой Для определения области интегрирования
Для определения области интегрирования следует спроецировать на плоскость
следует спроецировать на плоскость линию пересечения поверхностей, уравнение которой находится исключением
линию пересечения поверхностей, уравнение которой находится исключением Из данных уравнений. Вычитая одно уравнение из другого, получаем
Из данных уравнений. Вычитая одно уравнение из другого, получаем Это
Это

Так как
Уравнение параболы, лежащей в плоскости  С вершиной на оси
С вершиной на оси На расстоянии
На расстоянии от начала координат и пересекающей ось
от начала координат и пересекающей ось в точках
в точках Дуга указанной
Дуга указанной
Параболывместе с соответствующим отрезком оси Составляют границу области.
Составляют границу области.


Пример 19.18. Вычислить площадь поверхности конуса  , заключенной внутри цилиндра
, заключенной внутри цилиндра Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскости
Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскости На рис. 19.20 изображена только верхняя часть
На рис. 19.20 изображена только верхняя часть Вычислим пло
Вычислим пло
Ишь Этой части, проекция которой на плоскость
Этой части, проекция которой на плоскость Есть круг
Есть круг
Так как для рассматриваемой части конуса

То по формуле (19.19)
Получаем

Где – окружность
– окружность Переходя к полярным координатам, находим
Переходя к полярным координатам, находим

Следовательно, вся искомая площадь
Пример 19.19. Найти площадь поверхности, вырезанной цилиндром  Из сферы
Из сферы
Цилиндр вырезает из сферы две части, верхняя из них изображена на рис. 19.21. Вычислим площадь Поверхности этой сферы. Для верхней полусферы
Поверхности этой сферы. Для верхней полусферы

Следовательно,
 – круг
– круг
Переходя к полярным координатам, находим 338

Итак,


Рис. 19.20
Пример 19.20. Вычислить площадь частей сферы вырезанных из нее цилиндром
вырезанных из нее цилиндром Воспользовавшись параметрическими
Воспользовавшись параметрическими
Уравнениями сферической поверхности:


Рис. 19.21
Здесь вдет речь о вычислении площади верхнего и нижнего оснований «тела Вивиани» (см. рис. 19.19). Воспользуемся формулой (19.24), для чего предварительно найдем коэффициенты Так как
Так как
 То по формулам (19.25)
То по формулам (19.25)
Находим Следовательно,
Следовательно,
Ограничимся рассмотрением четверти изучаемой поверхности, лежащей в первом октанте. Для точек «кривой Вивиани», т. е. кривой пересечения сферы и цилиндра (в пределах первого октанта), Действительно подставляя выражения
Действительно подставляя выражения И
И Через
Через И
И В уравнение цилиндра
В уравнение цилиндра Получаем
Получаем  И поскольку для рассматриваемых точек, очевидно,
И поскольку для рассматриваемых точек, очевидно,  , то отсюда следует, что
, то отсюда следует, что
Установив на основании сказанного пределы изменения И
И По формуле (19.24) получим
По формуле (19.24) получим

| < Предыдущая | Следующая > |
|---|
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.

Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
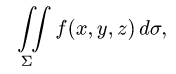
где  — часть поверхности, описываемая уравнением F(x,y,z) = 0
— часть поверхности, описываемая уравнением F(x,y,z) = 0
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием  на координатную плоскость XOY по формуле
на координатную плоскость XOY по формуле
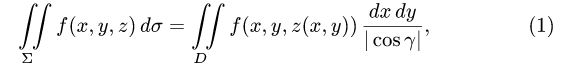
где D — проекция  на плоскость XOY,
на плоскость XOY, 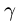 — угол между нормалью
— угол между нормалью
к поверхности  и осью OZ; z(x, у) определяем из уравнения поверхности F(x, у, z) = 0.
и осью OZ; z(x, у) определяем из уравнения поверхности F(x, у, z) = 0.
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем  на другую координатную плоскость или используем криволинейные координаты (можно
на другую координатную плоскость или используем криволинейные координаты (можно
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 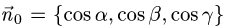 к поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
к поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
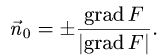
2.Проекцию D поверхности  на плоскость XOY находим, исключая z из условий, определяющих
на плоскость XOY находим, исключая z из условий, определяющих  .
.
3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Записываем ответ.
Пример:
Вычислить поверхностный интеграл
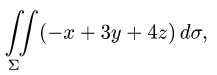
где  — часть плоскости
— часть плоскости
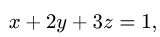
расположенная в первом октанте (т.е. 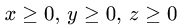 ).
).
Решение:
1.Единичные нормальные векторы 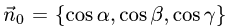 к по-
к по-
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
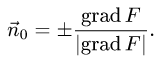
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
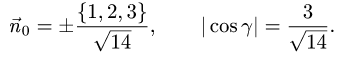
2.Поверхность  определяется условиями
определяется условиями
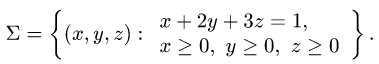
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих  :
:
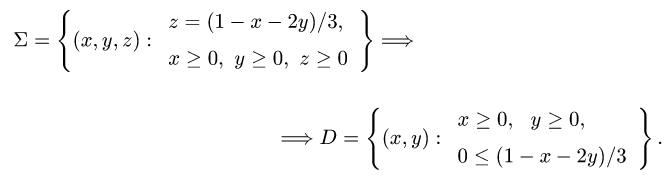
Отсюда
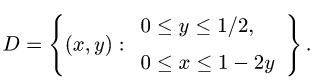
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
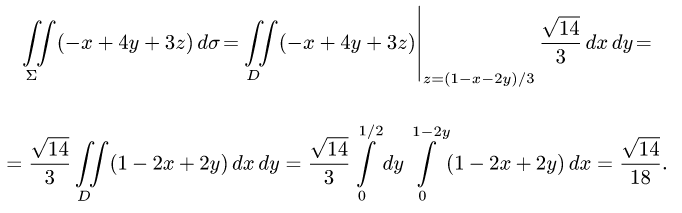
Ответ. 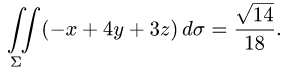
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
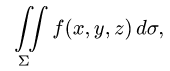
где  — часть поверхности
— часть поверхности 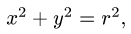 вырезаемая плоскостями
вырезаемая плоскостями
z = 0 и z = h.
План решения.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
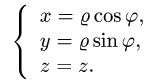
В этих координатах поверхность задается условиями
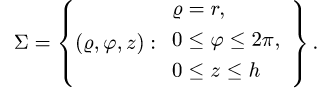
2.Так как
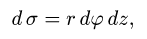
то
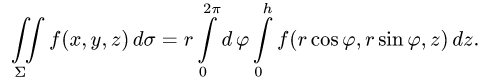
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
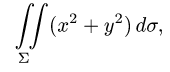
где  — часть поверхности
— часть поверхности 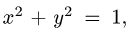 вырезаемая плоскостями
вырезаемая плоскостями
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
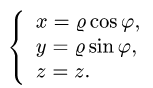
В этих координатах поверхность задается условиями
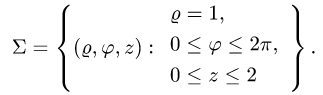
2.Так как 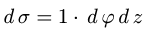 и
и 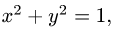 то имеем
то имеем
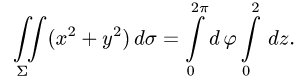
3.Вычисляем повторный интеграл:
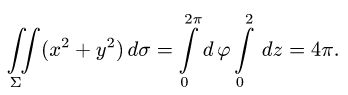
Ответ. 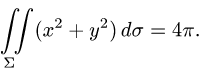
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
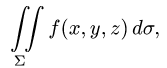
где 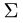 — верхняя полусфера
— верхняя полусфера
План решения.
1.Вводим на заданной поверхности (сфере) криволинейные координаты
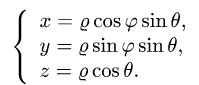
В этих координатах поверхность задается условиями
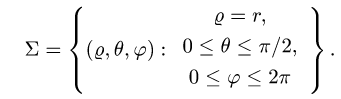
2.Так как 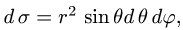 имеем
имеем
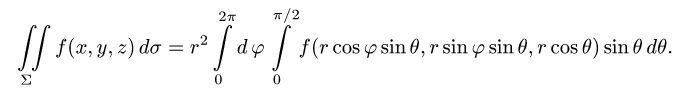
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
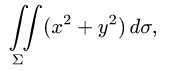
где 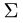 — верхняя полусфера
— верхняя полусфера
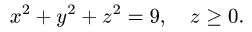
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
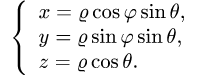
В этих координатах поверхность задается условиями
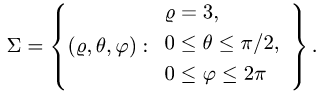
2.Так как 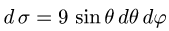 и
и 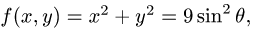 имеем
имеем
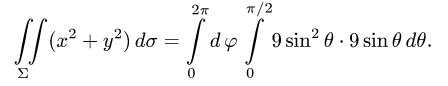
3.Вычисляем повторный интеграл:
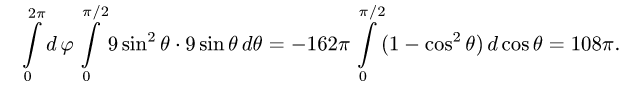
Ответ.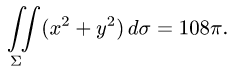
Определение и свойства поверхностных интегралов





Смотрите также:
Решение задач по математическому анализу
Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 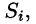 площади которых обозначим через ДSi (см. рис. 246), а диаметры — через
площади которых обозначим через ДSi (см. рис. 246), а диаметры — через 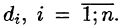 В каждой части
В каждой части 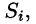 возьмем произвольную точку
возьмем произвольную точку 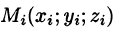 и составим сумму
и составим сумму

Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 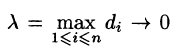 интегральная сумма (57.1) имеет пре-дел, то он называется поверхностным интегралом I рода от функции f(x;y;z) по поверхности S и обозначается
интегральная сумма (57.1) имеет пре-дел, то он называется поверхностным интегралом I рода от функции f(x;y;z) по поверхности S и обозначается 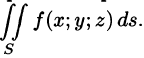
Таким образом, по определению,
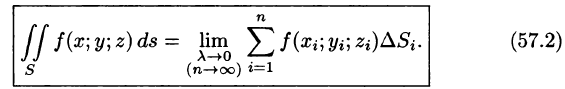
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
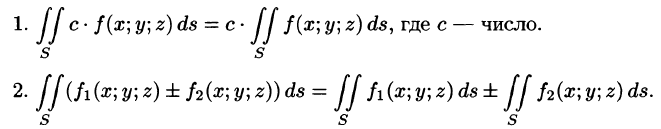
3. Если поверхность S разбить на части 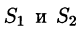 такие, что
такие, что 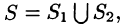 а пересечение
а пересечение 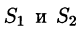 состоит лишь из границы, их разделяющей, то
состоит лишь из границы, их разделяющей, то
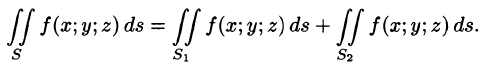
4.Если на поверхности S выполнено неравенство
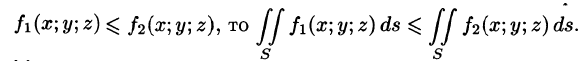
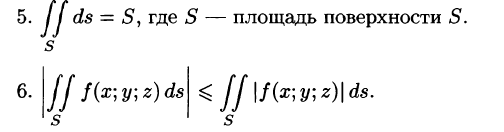
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка 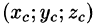 такая, что
такая, что
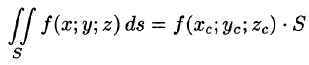
(теорема о среднем значении).
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем поверхность S на части 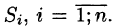 Обозначим через
Обозначим через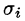 проекцию
проекцию 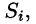 на плоскость Оху. При этом область D окажется разбитой на п частей
на плоскость Оху. При этом область D окажется разбитой на п частей 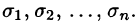 Возьмем в произвольную точку
Возьмем в произвольную точку 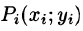 и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку
и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку 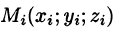 на поверхности
на поверхности  . Проведем в точке М, касательную плоскость и рассмотрим ту ее часть
. Проведем в точке М, касательную плоскость и рассмотрим ту ее часть 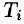 , которая на плоскость Оху проектируется в область
, которая на плоскость Оху проектируется в область 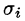 (см. рис. 247). Площади элементарных частей
(см. рис. 247). Площади элементарных частей 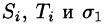 обозначим как
обозначим как 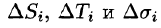 соответственно. Будем приближенно считать, что
соответственно. Будем приближенно считать, что

Обозначив через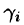 , острый угол между осью Oz и нормалью п, к поверхности в точке
, острый угол между осью Oz и нормалью п, к поверхности в точке 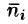 получаем:
получаем:
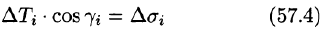
(область 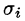 есть проекция
есть проекция 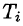 на плоскость Оху).
на плоскость Оху).
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 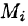 есть
есть
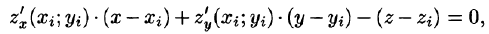
где 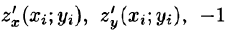 — координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами
— координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами 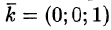 и
и
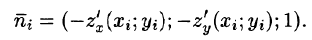
Следовательно,
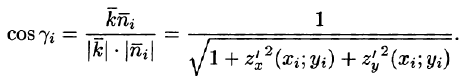
Равенство (57.4) принимает вид
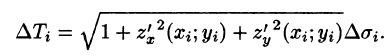
В правой части формулы (57.2) заменим 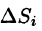 (учитывая (57.3)) на полученное выражение для
(учитывая (57.3)) на полученное выражение для 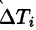 , a
, a 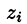 заменим на
заменим на 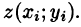 Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра
Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра  (а следовательно, и
(а следовательно, и 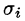 ), получаем формулу
), получаем формулу
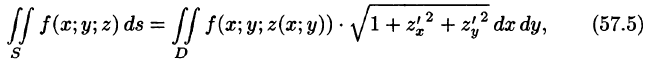
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
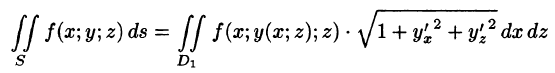
и
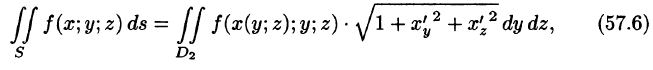
где 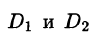 — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
— проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
Пример:
Вычислить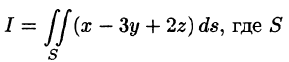 — часть плоскости
— часть плоскости 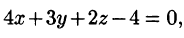 расположенной в I октанте (см. рис. 248).
расположенной в I октанте (см. рис. 248).
Решение:
Запишем уравнение плоскости в виде 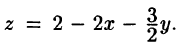
Находим 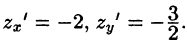 По формуле (57.5) имеем:
По формуле (57.5) имеем:
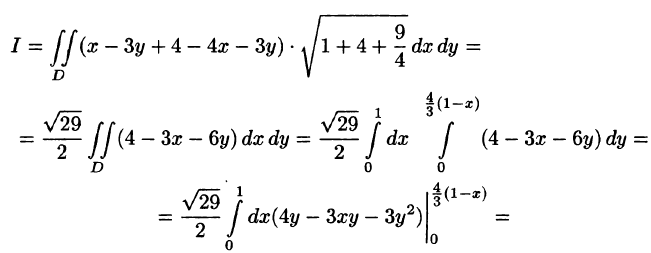
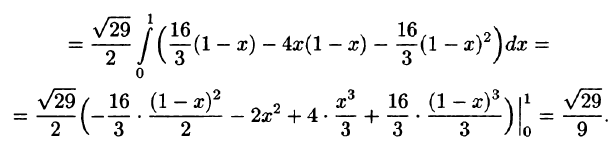
Пример:
Вычислить
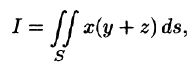
где S — часть цилиндрической поверхности 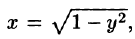 отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
Решение:
Воспользуемся формулой (57.6). Поскольку
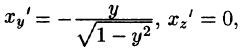
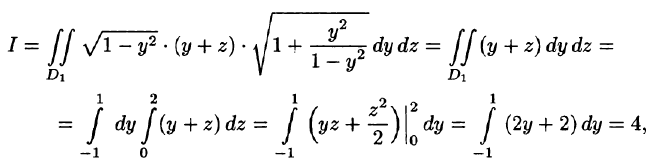
то где 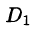 — прямоугольник
— прямоугольник 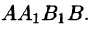
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
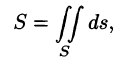
или
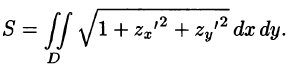
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы  Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 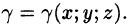 Для нахождения массы поверхности:
Для нахождения массы поверхности:
- Разбиваем поверхность S на п частей
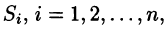 площадь которой обозначим
площадь которой обозначим 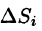 .
. - Берем произвольную точку
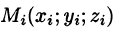 в каждой области
в каждой области  . Предполагаем, что в пределах области
. Предполагаем, что в пределах области 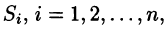 плотность постоянна и равна значению ее в точке
плотность постоянна и равна значению ее в точке 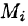 .
. - Масса
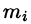 области
области мало отличается от массы
мало отличается от массы 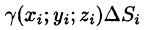 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью
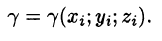
4. Суммируя 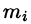 по всей области, получаем:
по всей области, получаем: 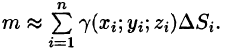
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей  , т. е.
, т. е.
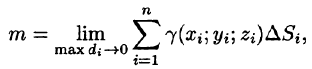
т. е.
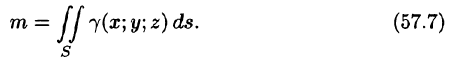
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
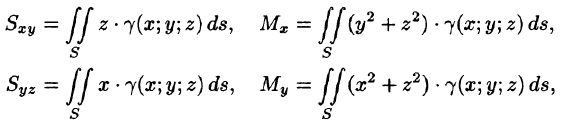
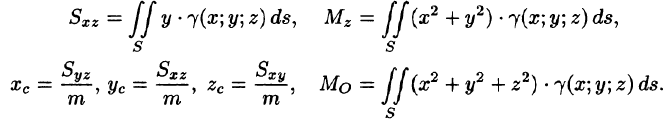
Пример:
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 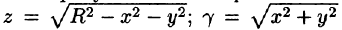 — поверхностная плотность полусферы.
— поверхностная плотность полусферы.
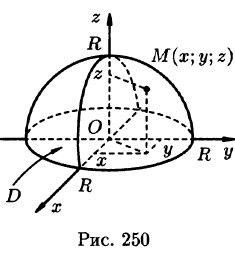
По формуле (57.7) находим:
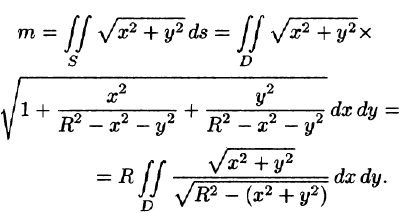
Переходим к полярным координатам:
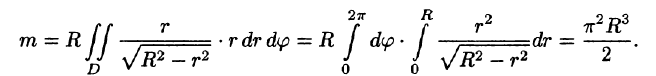
внутренний интеграл вычислен с помощью подстановки r= Rsint:
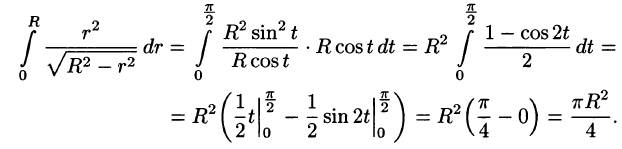
Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
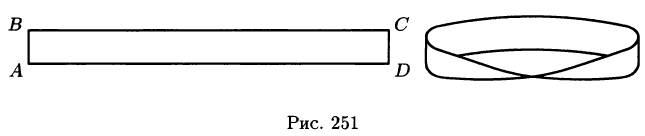
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 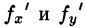 — функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).
— функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).
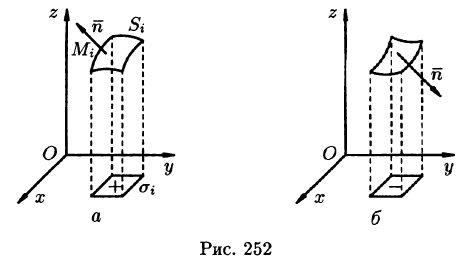
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части  , где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции
, где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции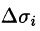 берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е.
берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е. 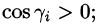 со знаком «минус», если выбрана нижняя сторона поверхности (или
со знаком «минус», если выбрана нижняя сторона поверхности (или 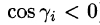 ) (см. рис. 252, б). В этом случае интегральная сумма имеет вид
) (см. рис. 252, б). В этом случае интегральная сумма имеет вид

где 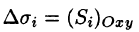 — площадь проекции
— площадь проекции  на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
Предел интегральной суммы (58.1) при 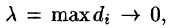 если он существует и не зависит от способа разбиения поверхности S на части
если он существует и не зависит от способа разбиения поверхности S на части  и от выбора точек
и от выбора точек 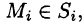 называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается
называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается
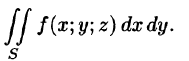
Итак
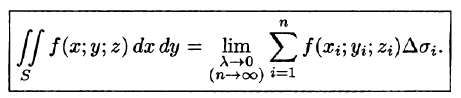
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
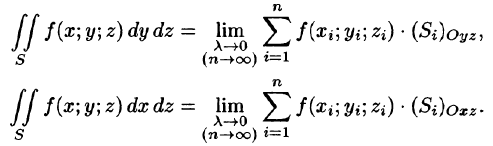
Общим видом поверхностного интеграла II рода служит интеграл
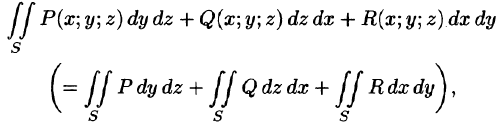
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 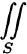 , по внутренней
, по внутренней 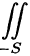 .
.
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям 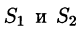 (аддитивное свойство), если
(аддитивное свойство), если 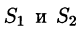 пересекаются лишь по границе, их разделяющей.
пересекаются лишь по границе, их разделяющей. - Если
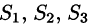 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
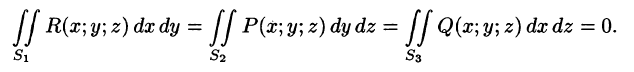
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 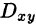 ) — проекции поверхности S на плоскость Оху.
) — проекции поверхности S на плоскость Оху.
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда 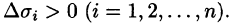
Так как 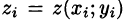 , то интегральная сумма (58.1) может быть записана в виде
, то интегральная сумма (58.1) может быть записана в виде
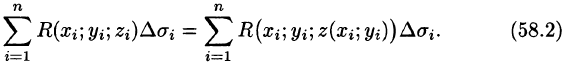
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 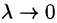 , получаем формулу
, получаем формулу
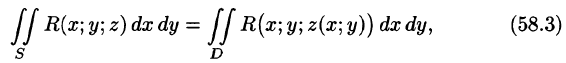
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
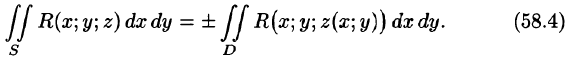
Аналогично
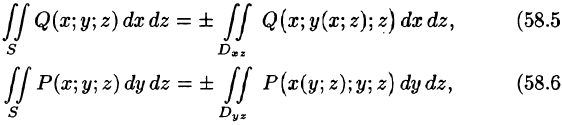
где 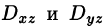 — проекции поверхности S на плоскости Oxz и Oyz соответственно (замкнутые области).
— проекции поверхности S на плоскости Oxz и Oyz соответственно (замкнутые области).
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
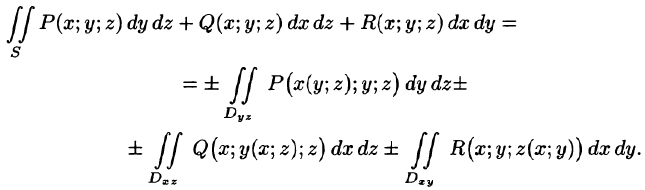
Замечание:
Можно показать справедливость равенств
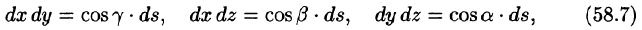
— элемент площади поверхности  — направляющие косинусы нормали n к выбранной стороне поверхности S.
— направляющие косинусы нормали n к выбранной стороне поверхности S.
Поверхностные интегралы I и II рода связаны соотношением
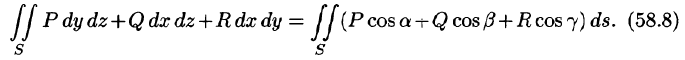
Пример:
Вычислить
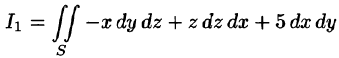
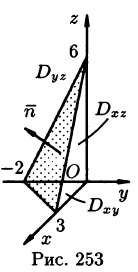
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 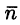 = (2; —3; 1) плоскости:
= (2; —3; 1) плоскости:
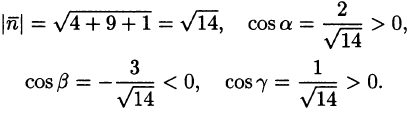
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
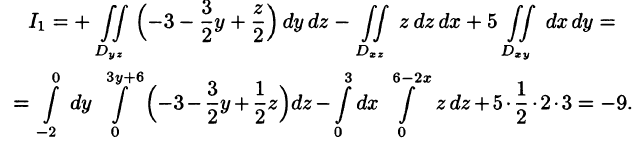
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
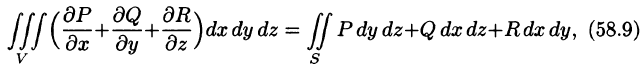
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
Пусть область V ограничена снизу поверхностью  , уравнение которой
, уравнение которой 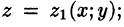 сверху — поверхностью
сверху — поверхностью 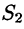 , уравнение которой
, уравнение которой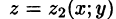 (функции
(функции 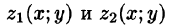 непрерывны в замкнутой области D — проекции V на плоскость
непрерывны в замкнутой области D — проекции V на плоскость 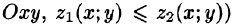 , сбоку — цилиндрической поверхностью
, сбоку — цилиндрической поверхностью 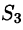 , образующие которой параллельны оси Oz (см. рис. 254).
, образующие которой параллельны оси Oz (см. рис. 254).
Рассмотрим тройной интеграл
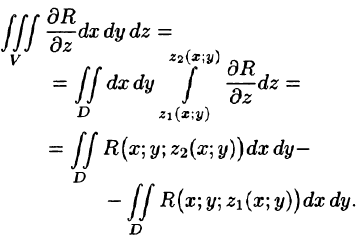
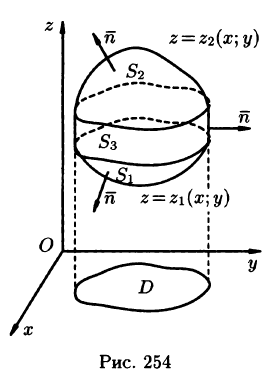
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 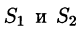 соответственно (см. (58.3)). Получаем:
соответственно (см. (58.3)). Получаем:
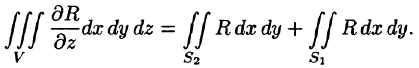
Добавляя равный нулю интеграл  по внешней стороне
по внешней стороне  (см. свойство 5 п. 58.1), получим:
(см. свойство 5 п. 58.1), получим:
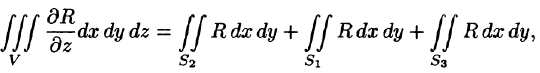
или
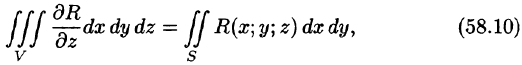
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
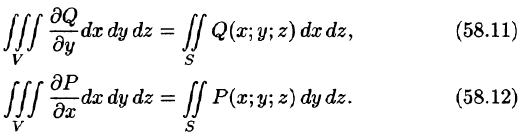
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример:
Вычислить
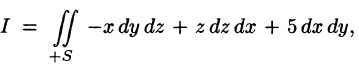
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
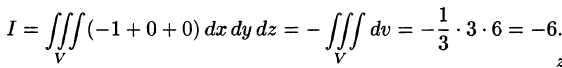
Заметим, что интеграл 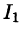 (см. пример 58.1) можно вычислить иначе:
(см. пример 58.1) можно вычислить иначе:
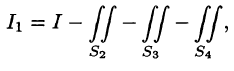
где поверхности 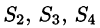 есть соответственно треугольники ОАС, АОВ, СОВ (см. рис. 255). Имеем:
есть соответственно треугольники ОАС, АОВ, СОВ (см. рис. 255). Имеем:
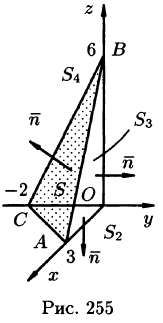
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
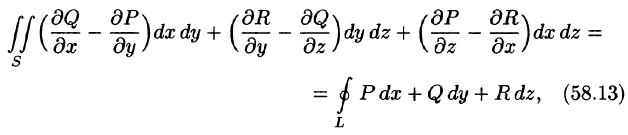
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции 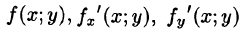 непрерывны в замкнутой области D (проекции поверхности S на плоскость Оху),
непрерывны в замкнутой области D (проекции поверхности S на плоскость Оху),  — граница области D (см. рис. 256).
— граница области D (см. рис. 256).
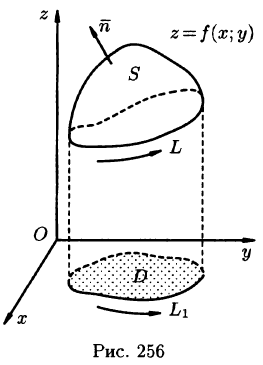
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида 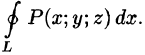
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на  . Интегральные суммы для криволинейных интегралов II рода по контурам
. Интегральные суммы для криволинейных интегралов II рода по контурам 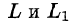 совпадают. Поэтому
совпадают. Поэтому
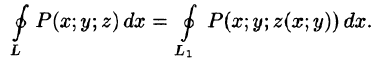
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
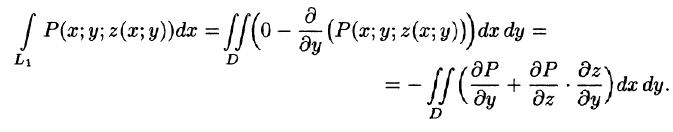
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
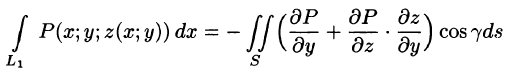
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е.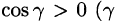 — острый угол между нормалью
— острый угол между нормалью 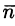 к поверхности S и осью Oz), то нормаль
к поверхности S и осью Oz), то нормаль 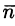 имеет проекции
имеет проекции 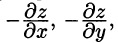 1. Направляющие косинусы пропорциональны соответствующим проекциям:
1. Направляющие косинусы пропорциональны соответствующим проекциям:
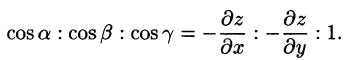
Отсюда 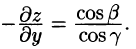 Тогда
Тогда
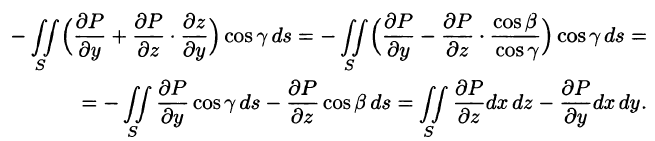
Следовательно,
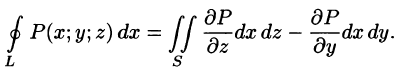
Аналогично получаются при соответствующих условиях еще два равенства:
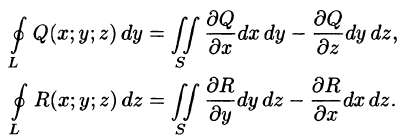
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
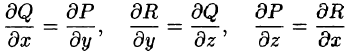
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
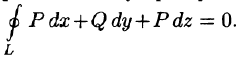
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
Пример:
Вычислить 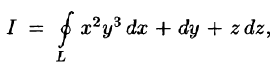 где контур L — окружность
где контур L — окружность 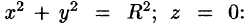 а) непосредственно,
а) непосредственно,
б) используя формулу Стокса, взяв в качестве поверхности полусферу 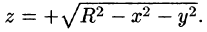
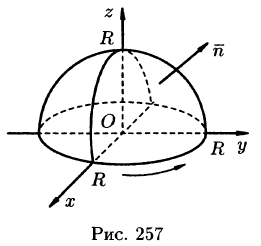
Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
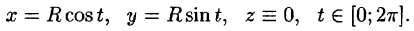
По формуле (56.7) имеем:
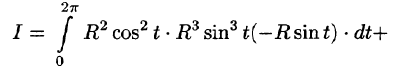
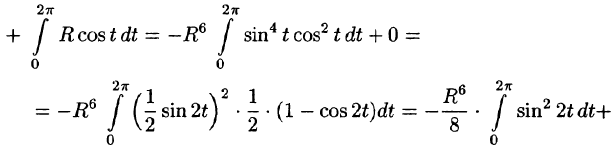
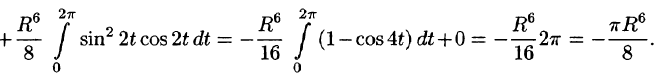
б) По формуле Стокса (58.13) находим:
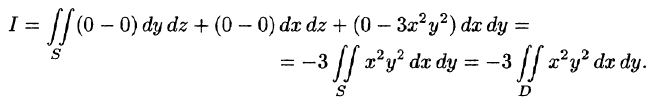
Переходя к полярным координатам, получаем:
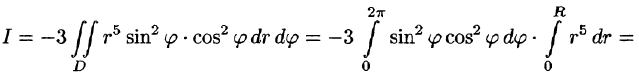
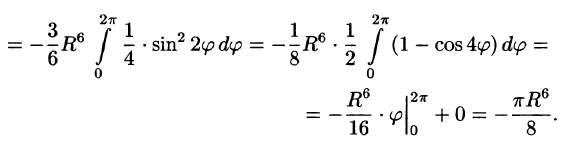
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью  снизу — поверхностью
снизу — поверхностью  сбоку — цилиндрической поверхностью
сбоку — цилиндрической поверхностью  , образующие которой параллельны оси Oz:
, образующие которой параллельны оси Oz:
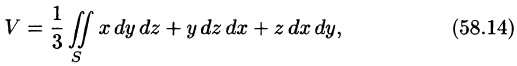
где 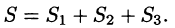
Действительно, положив в формуле Остроградского-Гаусса (58.9) 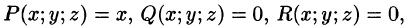 находим:
находим:
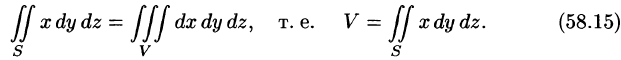
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:

Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу

выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

