
{S_{полн} = 2(ab+bc+ac)}
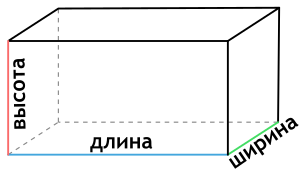
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Площадь поверхности параллелепипеда: онлайн-калькулятор
Для нахождения площади полной поверхности параллелепипеда необходимо рассчитать сумму площадей трех его граней и удвоить результат. Чтобы не совершать действия вручную и получить верный ответ быстро, воспользуйтесь нашим сервисом.
Наша компания помогает разобраться в задачах по алгебре и геометрии. Сервис работает без регистрации и оплаты. Автоматизированная программа производит последовательные вычисления, которые доступны для просмотра. Такая система позволяет избежать ошибок во время промежуточных действий.
Вычисление площади поверхности параллелепипеда. Онлайн-калькулятор
В программу заложен расчет площади поверхности параллелепипеда по формуле:

где a, b, h – ребра фигуры.
Для школьников сервис с основными математическими вычислениями – это возможность самостоятельно подготовиться к поступлению в ВУЗ. Число запросов на расчет не ограничивается, поэтому тренироваться в решении задач можно до полного усвоения темы. Формула в решении в совокупности с готовым чертежом ускоряет запоминание материала. Совершение вычислений не требуется оплачивать. Бесплатная помощь ученикам позволяет сэкономить на репетиторах и повысить успеваемость по математике.
Также сервис используют:
- студенты для подстраховки на зачетах и экзаменах. Готовое решение поможет быстро сориентироваться в задании.
- преподаватели во время проверки работ учеников. Также сервис дает возможность разнообразить план урока и подготовить для каждого ученика индивидуальное задание.
- инженеры и специалисты технических профессий, чтобы исключить погрешности в расчетах и оптимизировать рабочий процесс.
В разделе калькуляторов вы также найдете программы для нахождения площадей других фигур.
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
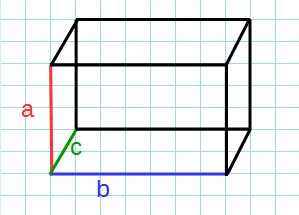
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
Прямоугольным параллелепипедом называется трехмерное тело, у которого противоположные грани параллельны и являются прямоугольниками. Проще говоря, прямоугольный параллелепипед представляет собой вытянутый куб.
Онлайн-калькулятор площади поверхности параллелепипеда
Прямоугольный параллелепипед можно охарактеризовать тремя числами — длинами его сторон: aa, bb, cc.
Формула площади поверхности параллелепипеда
Чтобы найти полную площадь поверхности параллелепипеда, нужно сложить площади всех его граней. Граней у параллелепипеда шесть, поэтому:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Но так как противоположные грани прямоугольного параллелепипеда равны между собой, то: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.
Поскольку гранями данного параллелепипеда являются прямоугольники, то их площади равны соответственно:
S1=S2=abS_1=S_2=ab
S3=S4=bcS_3=S_4=bc
S5=S6=acS_5=S_6=ac
Итак, полная площадь поверхности параллелепипеда:
S=2(ab+bc+ac)S=2(ab+bc+ac)
Из этой формулы следует, что если a=b=ca=b=c, то получим: S=6a2S=6a^2. Это и есть формула для площади поверхности куба со стороной aa.
Найдите площадь поверхности прямоугольного параллелепипеда со сторонами 2 см.2text{ см.}, 4 см.4text{ см.}, 6 см.6text{ см.}
Решение
a=2a=2
b=4b=4
c=6c=6
S=2(ab+bc+ac)=2(2⋅4+4⋅6+2⋅6)=88 (см. кв.)S=2(ab+bc+ac)=2(2cdot4+4cdot6+2cdot6)=88text{ (см. кв.)}
Ответ: 88 см. кв.88text{ см. кв.}
Найдите площадь поверхности прямоугольного параллелепипеда высотой 3 см.3text{ см.}, в основании которого лежит квадрат со стороной 1 см.1text{ см.}
Решение
a=b=1a=b=1
c=3c=3
S=2(ab+bc+ac)=2(1+3+3)=14 (см. кв.)S=2(ab+bc+ac)=2(1+3+3)=14text{ (см. кв.)}
Ответ: 14 см. кв.14text{ см. кв.}
Не знаете, где заказать задачу по геометрии? Обратитесь к нашим экспертам в данной области!
Тест по теме «Площадь поверхности параллелепипеда»
Напомним,
что призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Стороны
параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами
параллелепипеда. Две грани параллелепипеда называются противолежащими,
если они не имеют общего ребра.
Например,
грани и
–
противолежащие.
Грани,
имеющие общее ребро, называются смежными. Например, грани и
–
смежные, ребро у
них общее.
Иногда
какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями,
тогда остальные грани – боковыми гранями, а их стороны, соединяющие
вершины оснований параллелепипеда, – его боковыми рёбрами.
В
нашем случае у параллелепипеда грани
и
–
его основания. Остальные же грани являются боковыми гранями.
Две
вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий, противолежащие вершины, называется диагональю
параллелепипеда. У параллелепипеда всего четыре диагонали.
Объединение
боковых граней называется боковой поверхностью параллелепипеда, а
объединение всех граней называется полной поверхностью параллелепипеда.
Тогда площадью боковой поверхности параллелепипеда называется сумма
площадей его боковых граней.
А
площадью полной поверхности параллелепипеда называется сумма площадей
всех его граней.
Параллелепипед
обладает следующими свойствами:
1.
Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой
пополам.
3.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его
измерений.
Объём
параллелепипеда равен произведению площади основания на
высоту.
Объём
прямоугольного параллелепипеда равен произведению трёх
его измерений.
Куб
– это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани
которого – равные квадраты.
Диагональ
куба с ребром равна
.
Объём
куба
равен ,
где –
ребро куба.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. В основании прямого параллелепипеда лежит параллелограмм
с основаниями см
и см
и острым углом .
Боковое ребро параллелепипеда равно см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
вторая. Все грани параллелепипеда – ромбы с диагоналями см
и см.
Найдите площадь полной поверхности параллелепипеда.
Решение.
Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой см
со сторонами основания см
и см
и углом между ними .
Решение.
Задача
четвёртая. В прямоугольном параллелепипеде ребро
см,
см.
Найдите расстояние между диагональю параллелепипеда и
ребром .
Решение.
Задача
пятая. Две стороны основания параллелепипеда равны см
и см,
угол между ними .
Боковое ребро равно см
и наклонено к основанию под углом .
Найдите объём параллелепипеда.
Решение.
Задача
шестая. Все грани параллелепипеда – ромбы с периметром
равным и
острым углом .
Найдите объём параллелепипеда.
В ответ запишите значение .
Решение.
