Как найти площадь поверхности лопаты

Как найти площадь поверхности лопаты


Загрузить PDF


Загрузить PDF

Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
 Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.

  1. Изображение с названием Find Surface Area Step 1

    1

    Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]

    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 2

    2

    Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.

    • Запишите значение, обозначив его через а.
    • Например: а = 2 см

  3. Изображение с названием Find Surface Area Step 3

    3

    Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.

    • Сейчас вы вычислили значение площади одной из граней куба.
    • Например: а = 2 см
    • a2 = 2 х 2 = 4 см2

  4. Изображение с названием Find Surface Area Step 4

    4

    Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.

    • Это последний шаг в процессе вычисления площади поверхности куба.
    • Например: а 2 = 4 см2
    • SA = 6 х а2 = 6 х 4 = 24 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 5

    1

    Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
     Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.

    • Здесь а – ширина, b – высота, с – длина призмы.
    • Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 6

    2

    Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.

    • Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
    • Например: с = 5 см
    • Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
    • Например: а = 2 см
    • Измерьте высоту призмы; высоту обозначьте через b.
    • Например: b = 3 см

  3. Изображение с названием Find Surface Area Step 7

    3

    Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]

    • Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2

  4. Изображение с названием Find Surface Area Step 8

    4

    Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]

    • Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2

  5. Изображение с названием Find Surface Area Step 9

    5

    Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]

    • Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2

  6. Изображение с названием Find Surface Area Step 10

    6

    Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]

    • Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 11

    1

    Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]

    • Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
    • Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 12

    2

    Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]

    • Основание треугольника b – это его нижняя сторона.
    • Например: b = 4 см
    • Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
    • Например: h = 3 см
    • Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.

  3. Изображение с названием Find Surface Area Step 13

    3

    Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.

    • Например: Н = 5 см
    • Стороны треугольника – это три ребра одной (любой) из треугольных граней.
    • Например: а = 2 см, b = 4 см, с = 6 см

  4. Изображение с названием Find Surface Area Step 14

    4

    Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.

    • Например: P = а + b + с = 2 + 4 + 6 = 12 см

  5. Изображение с названием Find Surface Area Step 15

    5

    Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.

    • Например: Р х Н = 12 х 5 = 60 см2

  6. Изображение с названием Find Surface Area Step 16

    6

    Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]

    • Например: 2S + PH = 12 + 60 = 72 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 17

    1

    Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]

    • Здесь r – радиус шара, π ≈ 3,14.
    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 18

    2

    Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]

    • Например: r = 3 см

  3. Изображение с названием Find Surface Area Step 19

    3

    Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]

    • Например: r2 = r x r = 3 x 3 = 9 см2

  4. Изображение с названием Find Surface Area Step 20

    4

    Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
     Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]

    • Например: π*r2 = 3,14 x 9 = 28,26 см2

  5. Изображение с названием Find Surface Area Step 21

    5

    Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]

    • Например: 4π*r2 = 4 x 28,26 = 113,04 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 22

    1

    Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]

    • 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 23

    2

    Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
     Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.

    • Например: r = 3 см
    • Например: h = 5 см

  3. Изображение с названием Find Surface Area Step 24

    3

    Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]

    • Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
    • Например: 2π*r2 = 2 x 28,26 = 56,52 см2

  4. Изображение с названием Find Surface Area Step 25

    4

    Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]

    • Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2

  5. Изображение с названием Find Surface Area Step 26

    5

    Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]

    • Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 27

    1

    Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]

    • В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 28

    2

    Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]

    • Например: l = 3 см
    • Например: s = 1 см

  3. Изображение с названием Find Surface Area Step 29

    3

    Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]

    • Например: s2 = s х s = 1 х 1 = 1 см2

  4. Изображение с названием Find Surface Area Step 30

    4

    Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]

    • Например: 2 х s х l = 2 х 1 х 3 = 6 см2

  5. Изображение с названием Find Surface Area Step 31

    5

    Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]

    • Например: s2 + 2sl = 1 + 6 = 7 см2

    Реклама

  1. Изображение с названием Find Surface Area Step 32

    1

    Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]

    • Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.

  2. Изображение с названием Find Surface Area Step 33

    2

    Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]

    • Например: r = 2 см
    • Например: h = 4 см

  3. Изображение с названием Find Surface Area Step 34

    3

    Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]

    • Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см

  4. Изображение с названием Find Surface Area Step 35

    4

    Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]

    • Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2

  5. Изображение с названием Find Surface Area Step 36

    5

    Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]

    • Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см

  6. Изображение с названием Find Surface Area Step 37

    6

    Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]

    • Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2

    Реклама

Что вам понадобится

  • Линейка
  • Ручка или карандаш
  • Бумага

Об этой статье

Эту страницу просматривали 69 399 раз.

Была ли эта статья полезной?

Источник

Все формулы для площадей полной и боковой поверхности тел

1. Площадь полной поверхности куба

Площадь поверхности куба

a – сторона куба

Формула площади поверхности куба,(S):

Формула площади полной поверхности куба

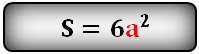
2. Найти площадь поверхности прямоугольного параллелепипеда

Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

Формула площади поверхности параллелепипеда

3. Найти площадь поверхности шара, сферы

Найти площадь поверхности шара

R – радиус сферы

π ≈ 3.14

Формула площади поверхности шара (S):

Формула площади поверхности сферы

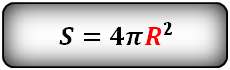
4. Найти площадь боковой и полной поверхности цилиндра

расчет площади поверхности цилиндра

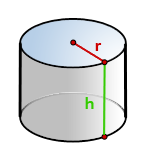
r – радиус основания

h – высота цилиндра

π ≈ 3.14

Формула площади боковой поверхности цилиндра, (Sбок):

Площадь боковой поверхности цилиндра

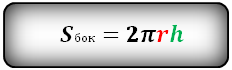
Формула площади всей поверхности цилиндра, (S):

Площадь всей поверхности цилиндра

5. Площадь поверхности прямого, кругового конуса

Площадь поверхности конуса

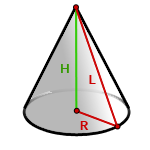
R – радиус основания конуса

H – высота

L – образующая конуса

π ≈ 3.14

Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади боковой поверхности конуса

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

Формула площади полной поверхности конуса

6. Формулы площади поверхности усеченного конуса

площадь поверхности усеченного конуса

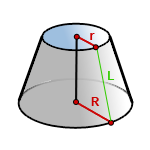
R – радиус нижнего основания

r – радиус верхнего основания

L – образующая усеченного конуса

π ≈ 3.14

Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади боковой поверхности усеченного конуса

Формула площади полной поверхности усеченного конуса, (S):

Формула площади полной поверхности усеченного конуса

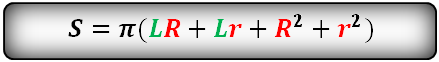
7. Площадь поверхности правильной пирамиды через апофему

Площадь поверхности правильной пирамиды

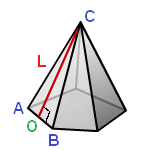
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)

P – периметр основания

Sосн – площадь основания

Формула площади боковой поверхности правильной пирамиды (Sбок):

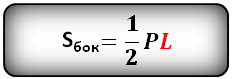
Формула площади боковой поверхности правильной пирамиды

Формула площади полной поверхности правильной пирамиды (S):

Формула площади полной поверхности правильной пирамиды

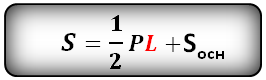
8. Площадь боковой поверхности правильной усеченной пирамиды

Площадь боковой поверхности правильной усеченной пирамиды

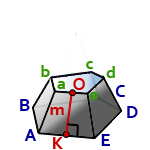
m – апофема пирамиды, отрезок OK

P – периметр нижнего основания, ABCDE

p – периметр верхнего основания, abcde

Формула площади боковой поверхности правильной усеченной пирамиды, (S):

Формула площади боковой поверхности правильной усеченной пирамиды

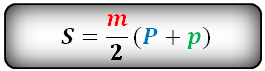
9. Площадь поверхности шарового сегмента

Площадь поверхности шарового сегмента

R – радиус самого шара

h – высота сегмента

π ≈ 3.14

Формула площади поверхности шарового сегмента, (S):

Формула площади поверхности шарового сегмента

10. Площадь поверхности шарового слоя

Площадь поверхности шарового слоя

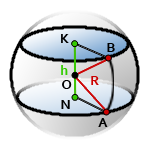
h – высота шарового слоя, отрезок KN

R – радиус самого шара

O – центр шара

π ≈ 3.14

Формула площади боковой поверхности шарового слоя, (S):

Формула площади боковой поверхности шарового слоя

11. Площадь поверхности шарового сектора

Площадь поверхности шарового сектора

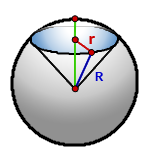
R – радиус шара

r – радиус основания конуса = радиус сегмента

π ≈ 3.14

Формула площади поверхности шарового сектора, (S):

Формула площади поверхности шарового сектора

Источник

Как определить площадь поверхности

Как на уроках математики, так и в различных практических делах регулярно приходится сталкиваться с необходимостью найти площадь той или иной поверхности. Это нужно при расчете количества материалов на строительстве, при планировке земельных участков, при изготовлении деталей на станке. Умение решать школьные геометрические задачи в этом случае оказываются очень кстати.

Как определить площадь поверхности

Вам понадобится

  • – геометрическое тело с заданными параметрами;
  • – измерительные приборы;
  • – формулы вычисления площади геометрических фигур.

Инструкция

Если нужно вычислить площадь поверхности пола прямоугольной комнаты или прямоугольного же земельного участка, измерьте их длину и ширину. Результаты перемножьте. В этом случае площадь поверхности вычисляется по формуле S=ab, где S – площадь поверхности, а и b — стороны прямоугольника. Формула площади квадрата будет выглядеть как S=a2.

Если плоская поверхность имеет более сложную форму, ее необходимо разделить на более простые части, формулы вычисления площади которых вам известны. Например, неправильный многоугольник можно разделить на треугольники или несколько треугольников и прямоугольник. При этом учитывайте заданные в условиях задачи параметры многоугольника.

Если вы имеете дело не с плоскостными фигурами, а с геометрическими телами, действовать необходимо точно так же. В условиях задачи обычно заданы параметры фигуры, которую надо построить или рассчитать. Внимательно прочитайте условия, какую именно площадь вам надо найти. Почти у каждого геометрического тела есть полная площадь поверхности, площадь боковой поверхности и площадь одного или двух оснований.

Вычислите площадь оснований. У конуса и пирамиды основание одно. Основание пирамиды представляет собой многоугольник и вычисляется по соответствующей формуле. Площадь основания правильной четырехугольной пирамиды вычислите по формуле площади квадрата, то есть возведя в квадрат длину одной из ее сторон. Если в основании пирамиды лежит сложный многоугольник, разделите его на более простые с известными вам параметрами. В основании конуса лежит круг, а соответственно, площадь рассчитывается по формуле S=πR2.

Найдите площадь боковой поверхности. У прямоугольного параллелепипеда она вычисляется по формуле S=p*h, где p – периметр прямоугольника основания, а h – высота. Площадь поверхности куба вычисляется по формуле S=4a2, поскольку боковая поверхность состоит из 4 квадратов.

Для вычисления боковой поверхности конуса удобнее всего сделать развертку. Найдите длину окружности по заданному радиусу. Она будет равна длине дуги боковой поверхности конуса. По длине дуги вычислите центральный угол, а затем радиус окружности, сектором которой является боковая поверхность конуса. Зная эти величины, найдите площадь сектора, то есть площадь боковой поверхности конуса.

Для определения полной поверхности того или иного геометрического тела сложите между собой площади боковой поверхности и оснований.

Полезный совет

Для того, чтобы более наглядно представить себе, что именно вам предстоит вычислить, очень удобно пользоваться развертками.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,651
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,896
  • разное
    16,900

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Калькуляторы площади от КАЛК.ПРО помогают определить значения для плоских (треугольника, многоугольника, круга…) и объемных фигур (цилиндра, конуса, сферы…), подсчитать площадь поверхности строительно-инженерных объектов (труб, воздуховодов, доски…), найти квадратуру земельных участков, стен, кровли и т. д. Все расчеты сопровождаются подробным описанием алгоритма, формулами и примерами. Результаты предоставляются в условных единицах или в единицах СИ.

Единицы измерения площади (СИ)

  • 1 мм2 (кв. миллиметр) = 0.000001 м2
  • 1 см2 (кв. сантиметр) = 0.0001 м2
  • 1 дм2 (кв. дециметр) = 0.01 м2
  • 1 А (ар/сотка) = 100 м2
  • 1 Га (гектар) = 10.000 м2
  • 1 км2 (кв. километр) = 1.000.000 м2

Для того чтобы начать расчет площади, выберите необходимый калькулятор:

Источник

Добавить комментарий