Как найти площадь тетраэдра
Тетраэдром в стереометрии называется многогранник, который состоит из четырёх треугольных граней. Тетраэдр имеет 6 рёбер и по 4 грани и вершины. Если у тетраэдра все грани являются правильными треугольниками, то и сам тетраэдр называется правильным. Площадь полной поверхности любого многогранника, в том числе и тетраэдра можно рассчитать, зная площади его граней.

Инструкция
Чтобы найти площадь полной поверхности тетраэдра, необходимо вычислить площадь треугольника составляющего его грань.
Если треугольник равносторонний, то его площадь равна
S = √3 * 4 / a², где a – ребро тетраэдра,
тогда площадь поверхности тетраэдра находится по формуле
S = √3 * a².
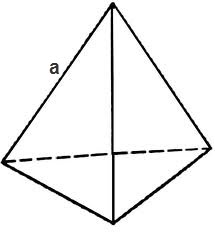
В случае, если тетраэдр является прямоугольным, т.е. все плоские углы при одной из его вершин являются прямыми, то площади трёх его граней являющихся прямоугольными треугольниками можно рассчитать по формуле
S = a * b *1/2,
S = a * c *1/2,
S = b * c *1/2,
площадь третьей грани можно рассчитать по одной из общих формул для треугольников, например по формуле Герона
S = √(p * (p – d) * (p – e) * (p – f)), где p = (d + e + f)/2 – полупериметр треугольника.
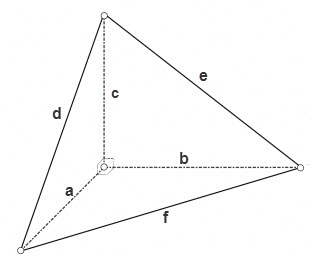
В общем случае, площадь любого тетраэдра можно рассчитать, используя формулу Герона для вычисления площадей каждой его грани.
Источники:
- площадь поверхности тетраэдра
- Найдите площадь сечения тетраэдра биссекторной плоскостью
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Правильные многогранники
Существует всего пять правильных многогранников:
- Тетраэдр
- Куб (Гексаэдр)
- Октаэдр
- Икосаэдр
- Додекаэдр
Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!
Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.
А также решим задачу №8.
О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».
Поехали!
Правильные многогранники — подробнее
Многогранник называется правильным, если:
- он выпуклый;
- все его грани являются правильными многоугольниками;
- в каждой его вершине сходится одинаковое число его ребер.
Пять правильных многогранников
Тетраэдр
Тетраэдр состоит из четырёх равносторонних треугольников.
Фигура имеет 4 грани, 4 вершины и 6 ребер(a).
Площадь поверхности тетраэдра:
( displaystyle S={{a}^{2}}sqrt{3})
Объем тетраэдра:
( displaystyle V=frac{{{a}^{3}}}{12}sqrt{2})
Радиус описанной вокруг тетраэдра сферы:
( displaystyle R=frac{a}{4}sqrt{6})
Радиус вписанной в тетраэдр сферы:
( displaystyle R=frac{a}{12}sqrt{6})
Куб (Гексаэдр)
Куб состоит из шести квадратов.
Фигура имеет 6 граней, 8 вершин и 12 ребер (a).
Площадь поверхности куба:
( displaystyle S=6{{a}^{2}})
Объем куба:
( displaystyle V={{a}^{3}})
Радиус описанной вокруг куба сферы:
( displaystyle R=frac{a}{2}sqrt{3})
Радиус вписанной в куб сферы:
( displaystyle r=frac{a}{2})
Октаэдр
Октаэдр составлен из восьми равносторонних треугольников.
Фигура имеет 8 граней, 6 вершин и 12 ребер (a).
Площадь поверхности октаэдра:
( displaystyle S=2{{a}^{2}}sqrt{3})
Объем октаэдра:
( displaystyle V=frac{{{a}^{3}}}{3}sqrt{2})
Радиус описанной вокруг октаэдра сферы:
( displaystyle R=frac{a}{2}sqrt{2})
Радиус вписанной в октаэдр сферы:
( displaystyle r=frac{a}{6}sqrt{6})
Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Фигура имеет 20 граней, 12 вершин и 30 ребер (a).
Площадь поверхности икосаэдра:
( displaystyle S=5{{a}^{2}}sqrt{3})
Объем икосаэдра:
( displaystyle V=frac{5{{a}^{3}}}{12}left( 3+sqrt{5} right))
Радиус описанной вокруг икосаэдра сферы:
( displaystyle R=frac{a}{4}sqrt{2left( 5+sqrt{5} right)})
Радиус вписанной в икосаэдр сферы:
( displaystyle r=frac{a}{4sqrt{3}}left( 3+sqrt{5} right))
Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Фигура имеет 12 граней, 20 вершин и 30 ребер (a).
Площадь поверхности додекаэдра:
( displaystyle S=3{{a}^{2}}sqrt{5left( 5+2sqrt{5} right)})
Объем додекаэдра:
( displaystyle V=frac{{{a}^{3}}}{4}left( 15+7sqrt{5} right))
Радиус описанной вокруг додекаэдра сферы:
( displaystyle R=frac{a}{4}left( 1+sqrt{5} right)sqrt{3})
Радиус вписанной в додекаэдр сферы:
( displaystyle r=frac{a}{4}sqrt{10+frac{22}{sqrt{5}}})
Решение задачи №8 на тему «Правильные многогранники»
Задача:
В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( displaystyle sqrt{12}) найдите ( displaystyle A{{C}_{1}}).
Решение:
![]()
( displaystyle d=asqrt{3}),
где ( displaystyle d) – диагональ куба,( displaystyle a) – сторона куба.( displaystyle A{{C}_{1}}) – это и есть диагональ куба.
Тогда ( displaystyle A{{C}_{1}}=asqrt{3}=sqrt{12}cdot sqrt{3}=sqrt{36}=6).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 декабря 2019 года; проверки требуют 8 правок.
| Правильный тетраэдр | |||
|---|---|---|---|
 |
|||
 |
|||
| Тип | правильный многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | правильные треугольники | ||
| Конфигурация вершины | 3.3.3 | ||
| Двойственный многогранник | тоже правильный тетраэдр | ||
| Классификация | |||
| Символ Шлефли | {3,3} | ||
| Группа симметрии |
 |
||
| Количественные данные | |||
| Длина ребра |
 |
||
| Площадь поверхности |
 |
||
| Объём |
 |
||
| Телесный угол при вершине |
 ср ср |
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.
Свойства правильного тетраэдра[править | править код]
- Каждая его вершина является вершиной трех равносторонних треугольников. А значит, сумма плоских углов при каждой вершине будет равна
.
- В правильный тетраэдр можно вписать октаэдр, притом четыре из восьми граней октаэдра будут совмещены с серединными треугольниками четырёх граней тетраэдра, а все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Правильный тетраэдр можно вписать в куб, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба, а все шесть рёбер тетраэдра будут совмещены с диагоналями граней куба.
Интересные факты[править | править код]
Середины граней правильного тетраэдра также образуют правильный тетраэдр.
Соотношения:
- рёбер и высот правильных тетрадров, радиусов переписанных, описанных и писанных сфер соответственно равны
;
- площадей поверхности равно
;
- объёмов равно
.

Autodualité du tétraèdre régulier.
Примечания[править | править код]
- ↑ 1 2 3 4 5 Coxeter, 1948.
Литература[править | править код]
- Harold Scott MacDonald Coxeter. Table I(i) // Regular Polytopes. — Methuen and Co., 1948.
Тетраэдр – это уникальная пирамида с равносторонним треугольником в основании, которое идентично боковым граням. Таким образом, у тетраэдра всего четыре треугольные грани, которые конгруэнтны между собой – и это главное условие для правильных многогранников, ряд которых открывает тетраэдр. Площадь боковой поверхности тетраэдра будет равна трем площадям треугольников, а площадь полной поверхности тетраэдра – четырем. Для их нахождения достаточно знать всего лишь сторону треугольника:

