Как найти площадь основания параллелепипеда
Основанием параллелепипеда всегда является параллелограмм. Для того чтобы найти площадь основания, вычислите площадь этого параллелограмма. Как частный случай, это может быть прямоугольник или квадрат. Также можно найти площадь основания параллелепипеда, зная его объем и высоту.

Вам понадобится
- Линейка, транспортир, инженерный калькулятор
Инструкция
В общем случае основание параллелепипеда представляет собой параллелограмм. Чтобы найти его площадь, с помощью линейки произведите измерение длин его сторон, а транспортиром измерьте угол между ними. Площадь основания параллелепипеда будет равна произведению этих сторон на синус угла между ними S=a • b • Sin(α).
Чтобы определить площадь основания параллелепипеда другим способом, измерьте одну из сторон основания, затем опустите на нее высоту из вершины, которая лежит напротив этой стороны. Измерьте длину этой высоты. Для получения площади основания найдите площадь параллелограмма, умножив длину стороны на высоту, которая на нее опущена S=a • h.
Для получения значения площади другим способом измерьте длины его диагоналей (расстояния между противоположными вершинами), и угол между диагоналями. Площадь будет равна половине произведения диагоналей на синус угла между ними S=0,5•d1•d2•Sin(β).
Для параллелепипеда, в основании которого лежит ромб, достаточно измерить длины его диагоналей и найти половину их произведения S=0,5 • d1 • d2.
В том случае, когда основание параллелепипеда представляет собой прямоугольник, измерьте длину и ширину этой геометрической фигуры, затем перемножьте эти значения S=a • b. Это и будет площадь его основания. В том случае, когда основание – квадрат, измерьте одну его сторон и возведите во вторую степень S=a².
Если известен объем параллелепипеда, измерьте его высоту. Для этого опустите перпендикуляр из любой вершины верхнего основания на плоскость, к которой принадлежит нижнее основание. Измерьте длину этого отрезка, являющегося высотой параллелепипеда. Если параллелепипед прямой (его боковые ребра перпендикулярны основаниям), достаточно измерить длину одного из этих ребер, которое равно высоте параллелепипеда. Для получения площади основания, объем параллелепипеда поделите на его высоту S=V/h.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
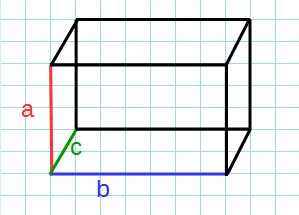
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
Площадь поверхности параллелепипеда
Содержание:
- Что такое площадь поверхности параллелепипеда
- Формула нахождения полной площади
- Вычисление площади боковой поверхности прямоугольного параллелепипеда
- Примеры решения задач
Что такое площадь поверхности параллелепипеда
Определение
Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.
В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.
Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула нахождения полной площади
В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:
(S=2cdot(acdot b+acdot c+bcdot c))
где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA1B1C1D1.
Полная площадь его поверхности равняется сумме площадей всех граней: (S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1})
Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:
(S_{пар}=2cdotleft(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}right))
Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:
(S_▭=acdot b)
У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA1. Для удобства обозначим их как a, b и c соответственно.
Таким образом:
(S_{ABCD}=acdot b)
(S_{AA_1D_1D}=acdot c)
(S_{BB_1A_1A}=bcdot c)
Подставим данные значения в обозначенную выше формулу площади параллелепипеда:
(S_{пар}=2cdotleft(acdot b+acdot c+bcdot cright))
Вычисление площади боковой поверхности прямоугольного параллелепипеда
Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.
Для этого есть три взаимосвязанные формулы:
- (S_{бок}=P_{осн}cdot h,) где (P_{осн}) — периметр основания параллелепипеда; h — высота. На рисунке выше она равняется стороне, обозначенной как c.
- (S_{бок}=2cdot acdot c+2cdot bcdot c), где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
- (S_{бок}=2cdot ccdot(a+b).)
Примеры решения задач
Задача
Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA1B1C1D1.
Дано: AB = 3, A1B = 6, AD = 5.
Решение
Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA1. Так как длина диагонали A1B известна, сделать это нетрудно.
Воспользуемся теоремой Пифагора:
(A_1B=sqrt{{AA_1}^2+{AB}^2})
Соответственно, ({AA_1}=sqrt{{A_1B}^2-{AB}^2}=sqrt{6^2-3^2}=sqrt{36-9}=sqrt{25}=5)
Подставим известные значения в формулу расчета площади поверхности:
(S=2cdot(acdot b+acdot c+bcdot c))
(S=2cdot(ABcdot AD+ABcdot AA_1+ADcdot AA_1)=2cdot(3cdot5+3cdot5+5cdot5)=2cdot(15+15+25)=2cdot55=110)
Ответ: S=110.
Задача 2
Вычислить длину стороны прямого параллелепипеда ABCDA1B1C1D1.
Дано: Sпов=96, Sбок=60, b=6.
Решение
Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:
(S=acdot b)
Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:
(S_{пов}-S_{бок}=2cdot acdot b+2cdot acdot c+2cdot bcdot c-2cdot acdot c-2cdot bcdot c=2cdot acdot b)
Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:
(2cdot acdot b=S_{пов}-S_{бок})
(a=frac{S_{пов}-S_{бок}}{2cdot b}=frac{96-60}{2cdot6}=frac{36}{12}=3)
Ответ: a=3.
Насколько полезной была для вас статья?
Рейтинг: 4.00 (Голосов: 7)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
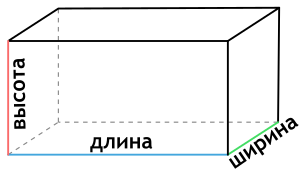
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Площадь поверхности параллелепипеда
Алик Беникович Айрапетян
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как выглядят формулы для расчёта полной и боковой площади поверхности параллелепипеда. Также на страницу добавлен онлайн-калькулятор для расчёта площади прямоугольного параллелепипеда.
Определение 1
Параллелепипед является разновидностью призмы, основания которой представляют собой параллелограммы. Также параллелепипедами называют призмы, в основании которых лежат многогранники, а все грани являются параллелограммами.
Наиболее знакомый всем вид параллелепипеда — это прямоугольный параллелепипед. Все его грани являются прямоугольниками.
Для расчёта полной площади прямоугольного параллелепипеда введите значение сторон и высоты в поля для ввода.
Площадь поверхности параллелепипеда через стороны

Для прямоугольного параллелепипеда площадь поверхности определяется по формуле:
$S = 2 cdot (a cdot b + b cdot h + a cdot h)$, здесь
$a, b$ — стороны основания параллелепипеда;
$h$ — высота параллелепипеда.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Разберём пример на нахождение полной площади параллелепипеда.
Пример 1
Задача
Стороны основания прямоугольного параллелепипеда равны $a = 3$ см и $b = 7$ см, а его высота $h$ равна $4$ см. Чему равна полная площадь поверхности параллелепипеда?
Решение:
Воспользуемся вышеприведённой формулой:
$S = 2 cdot (3 cdot 4 + 7 cdot 4 + 3 cdot 7) = 122$ кв. см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ найден верно.
Также используя следующий онлайн-калькулятор, вы сможете рассчитать площадь боковой поверхности прямоугольного параллелепипеда.
Площадь боковой поверхности прямоугольного параллелепипеда через стороны

Площадь боковой поверхности прямоугольного параллелепипеда определяется по формуле:
$S = 2 cdot h cdot (a + b)$, где
$h$ — длина ребра параллелепипеда;
$a, b$ — стороны основания.
Рассчитаем для примера площадь боковой поверхности для параллелепипеда из предыдущей задачи.
Пример 2
Задача
$a = 3$ см, $b = 7$ см, а высота $h = 4$ см. Чему равна боковая площадь поверхности прямоугольного параллелепипеда?
Решение:
$S_б = 2 cdot 4 cdot (3 + 7) = 80$ кв. см.
Решение соответствует решению, полученному с помощью онлайн-калькулятора, а значит, ответ правильный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 18.06.2019

