Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
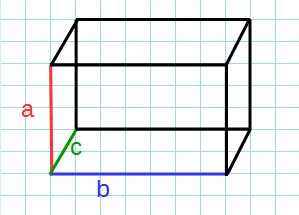
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
Прямоугольным параллелепипедом называется трехмерное тело, у которого противоположные грани параллельны и являются прямоугольниками. Проще говоря, прямоугольный параллелепипед представляет собой вытянутый куб.
Онлайн-калькулятор площади поверхности параллелепипеда
Прямоугольный параллелепипед можно охарактеризовать тремя числами — длинами его сторон: aa, bb, cc.
Формула площади поверхности параллелепипеда
Чтобы найти полную площадь поверхности параллелепипеда, нужно сложить площади всех его граней. Граней у параллелепипеда шесть, поэтому:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Но так как противоположные грани прямоугольного параллелепипеда равны между собой, то: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.
Поскольку гранями данного параллелепипеда являются прямоугольники, то их площади равны соответственно:
S1=S2=abS_1=S_2=ab
S3=S4=bcS_3=S_4=bc
S5=S6=acS_5=S_6=ac
Итак, полная площадь поверхности параллелепипеда:
S=2(ab+bc+ac)S=2(ab+bc+ac)
Из этой формулы следует, что если a=b=ca=b=c, то получим: S=6a2S=6a^2. Это и есть формула для площади поверхности куба со стороной aa.
Найдите площадь поверхности прямоугольного параллелепипеда со сторонами 2 см.2text{ см.}, 4 см.4text{ см.}, 6 см.6text{ см.}
Решение
a=2a=2
b=4b=4
c=6c=6
S=2(ab+bc+ac)=2(2⋅4+4⋅6+2⋅6)=88 (см. кв.)S=2(ab+bc+ac)=2(2cdot4+4cdot6+2cdot6)=88text{ (см. кв.)}
Ответ: 88 см. кв.88text{ см. кв.}
Найдите площадь поверхности прямоугольного параллелепипеда высотой 3 см.3text{ см.}, в основании которого лежит квадрат со стороной 1 см.1text{ см.}
Решение
a=b=1a=b=1
c=3c=3
S=2(ab+bc+ac)=2(1+3+3)=14 (см. кв.)S=2(ab+bc+ac)=2(1+3+3)=14text{ (см. кв.)}
Ответ: 14 см. кв.14text{ см. кв.}
Не знаете, где заказать задачу по геометрии? Обратитесь к нашим экспертам в данной области!
Тест по теме «Площадь поверхности параллелепипеда»

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
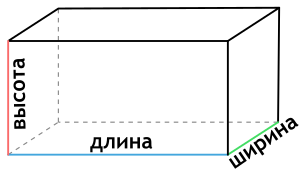
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Площадь поверхности параллелепипеда: онлайн-калькулятор
Для нахождения площади полной поверхности параллелепипеда необходимо рассчитать сумму площадей трех его граней и удвоить результат. Чтобы не совершать действия вручную и получить верный ответ быстро, воспользуйтесь нашим сервисом.
Наша компания помогает разобраться в задачах по алгебре и геометрии. Сервис работает без регистрации и оплаты. Автоматизированная программа производит последовательные вычисления, которые доступны для просмотра. Такая система позволяет избежать ошибок во время промежуточных действий.
Вычисление площади поверхности параллелепипеда. Онлайн-калькулятор
В программу заложен расчет площади поверхности параллелепипеда по формуле:

где a, b, h – ребра фигуры.
Для школьников сервис с основными математическими вычислениями – это возможность самостоятельно подготовиться к поступлению в ВУЗ. Число запросов на расчет не ограничивается, поэтому тренироваться в решении задач можно до полного усвоения темы. Формула в решении в совокупности с готовым чертежом ускоряет запоминание материала. Совершение вычислений не требуется оплачивать. Бесплатная помощь ученикам позволяет сэкономить на репетиторах и повысить успеваемость по математике.
Также сервис используют:
- студенты для подстраховки на зачетах и экзаменах. Готовое решение поможет быстро сориентироваться в задании.
- преподаватели во время проверки работ учеников. Также сервис дает возможность разнообразить план урока и подготовить для каждого ученика индивидуальное задание.
- инженеры и специалисты технических профессий, чтобы исключить погрешности в расчетах и оптимизировать рабочий процесс.
В разделе калькуляторов вы также найдете программы для нахождения площадей других фигур.
