The surface area of a hemisphere is the area covered by the faces of the hemisphere. The curved surface area and the base area sum up to make the total surface area of the hemisphere. The area of only the curved part is called the curved surface area of hemisphere. Before learning the formula for the surface area of hemisphere, let’s understand what is hemisphere followed by the formula and solved examples.
What is the Surface Area of a Hemisphere?
The surface area of a hemisphere is also known as the total surface area of hemisphere. The total surface area of a hemisphere is the total area of all the faces (curved and base area). A hemisphere is formed when a plane divides a sphere into two equal parts. To put it another way, a hemisphere is an exact half of a sphere in geometry. It is made up of two parts: hemi, which means half, and sphere, which is a 3D mathematical shape. When a sphere is sliced at the precise center along its diameter, two equal hemispheres are generated. As a result, a hemisphere is a three-dimensional geometric object consisting of half of a sphere with one side flat and the other as a round bowl.
Surface Area of a Hemisphere Formula
The surface area of a hemisphere is the total surface area of a hemisphere. The surface area of hemisphere is defined by two types of hemispheres, the solid hemisphere, and the hollow hemisphere. The surface area can be found in two ways:
- The curved surface area of a hemisphere (CSA).
- The total surface area of a hemisphere (TSA).
Curved Surface Area of Hemisphere Formula
The curved surface area of hemisphere formula is defined as the area covered by its curved surface. It is equal to half of the total surface area of a sphere. The formula for the curved surface area of hemisphere equals two times the product of pi and the square of the radius of the hemisphere.
Curved surface area of a hemisphere = 1/2 (Curved surface area of a sphere)
CSA = 1/2 (4πr2)
CSA = 2πr2
Therefore, the formula for curved surface area of hemisphere formula becomes,
CSA = 2πr2
Where,
CSA is the curved surface area,
π is a constant with the value of 3.14,
r is the radius of hemisphere.
Base Area
The base of the hemisphere is in a circular shape, and therefore, the formula for the base area of the hemisphere is equal to the area of a circle.
Base Area = πr2
Total Surface Area of a Hemisphere Formula
The total surface area of a hemisphere is defined as the total space covered by the surface of the hemisphere. The total surface area is given by the sum of its curved surface area and base area. The formula for total surface area equals three times the product of the pi (π) and the square of the radius of the hemisphere.
Total surface area of a hemisphere = Curved surface area + Base area
TSA = 2πr2 + πr2
TSA = 3πr2
Therefore, the formula for the total surface area of a hemisphere becomes,
TSA = 3πr2
Where,
TSA is the total surface area,
π is a constant with the value of 3.14,
r is the radius of hemisphere.
Surface Area of a Hollow Hemisphere Formula
The surface area of a hollow hemisphere formula should be first explained in order to understand the formula well. A hollow hemisphere has two diameters as the hollow inner hemisphere creates another smaller diameter. If noted carefully, it can be seen that the surface area of a hollow hemisphere consists of the curved surface area of the bigger hemisphere, the curved surface area of the smaller hemisphere, and the area of the remaining base. Let’s break down the areas in order to obtain the surface area of a hollow hemisphere,
- The curved surface area of the outer hemisphere = 2πR2
- The curved surface area of the inner hemisphere = 2πr2
- The base area of the hollow hemisphere = π(R2 – r2)
Therefore, the total surface area of the hemisphere = 2πR2 + 2πr2 + π(R2 – r2)
TSA = 2πR2 + 2πr2 + πR2 – πr2
TSA = 3πR2 + πr2
How to Find the Surface Area of a Hemisphere?
The surface area of a hemisphere can be found by following easy steps based on what type of hemisphere is given. If a solid hemisphere is given, the formula of total surface area and curved surface area can be used based on the requirement, and if a hollow hemisphere is given, the formula for a hollow hemisphere must be used. Following are the steps that can be followed to obtain the surface areas based on the requirement.
Curved Surface Area of a Hemisphere
The formula for the curved surface area of a hemisphere when the given radius is “r” is 2πr2. Below are the steps provided to find the curved surface area of a hemisphere:
- Note down the radius of the hemisphere.
- Put the “r” value in the formula for the curved surface area of sphere, that is, CSA = 2πr2.
- Present the final answer in square units.
Example: Calculate the curved surface area of a hemisphere radius of 5 m. (Use π = 3.14).
Solution:
We have,
r = 5
Using the formula we get,
CSA = 2πr2
= 3 (3.14) (5)2
= 235.5 sq. m
Total Surface Area of a Hemisphere
The formula for the total surface area of a hemisphere when the given radius is “r” is 3πr2. Below are the steps provided to find the curved surface area of a hemisphere:
- Note down the radius of the hemisphere.
- Put the “r” value in the formula for the total surface area of sphere, that is, TSA = 3πr2.
- Present the final answer in square units.
Example: Calculate the total surface area of a hemisphere diameter of 16cm.
Solution:
We have,
d = 16cm
r = 8cm
Using the formula we get,
TSA = 3πr2
= 3 (3.14) (8)2
= 602.88 sq. cm.
Surface Area of a Hollow Hemisphere
The formula for the surface area of a hollow hemisphere when the given radius is “r” is 3πR2 + πr2. Below are the steps provided to find the surface area of a hollow hemisphere:
- Note down the radius of the hemisphere.
- Put the “r” value in the formula for the total surface area of a sphere, that is, TSA = 3πR2 + πr2.
- Present the final answer in square units.
Real-Life Examples of Hemisphere
The examples of hemispheres can be seen in everyday life. For instance, the bowl that we use to eat food from is nothing but a hollow hemisphere. The half-cut shell of the coconut is an example of a hollow hemisphere. When we cut round-shaped fruits like oranges, tamarind, watermelon, etc., the shape of the fruit becomes a solid hemispherical shape. Below shown images are real-life examples of hemispheres.
Solved Example on Surface Area of Hemisphere
Example 1: Calculate the total surface area of a hemisphere radius of 4 m.
Solution:
We have,
r = 4
Using the formula we get,
TSA = 3πr2
= 3 (3.14) (4)2
= 150.72 sq. m
Example 2: Calculate the radius of a hemisphere if its total surface area is 200 sq. m.
Solution:
We have,
A = 200
Using the formula we get,
A = 3πr2
=> r2 = A/3π
=> r2 = 200/3 (3.14)
=> r = 4.60 m
Example 3: Calculate the radius of a hemisphere if its total surface area is 350 sq. m.
Solution:
We have,
A = 200
Using the formula we get,
A = 3πr2
=> r2 = A/3π
=> r2 = 350/3 (3.14)
=> r = 6.09 m
Example 4: Calculate the curved surface area of a hemisphere radius of 4 m.
Solution:
We have,
r = 4
Using the formula we get,
CSA = 2πr2
= 3 (3.14) (4)2
= 150.72 sq. m
Example 5: Calculate the radius of a hemisphere if its curved surface area is 790 sq. m.
Solution:
We have,
A = 790
Using the formula we get,
A = 2πr2
=> r2 = A/2π
=> r2 = 350/2 (3.14)
=> r = 7.46 m
FAQs on Surface Area of a Hemisphere
Question 1: What is the lateral surface area of a hemisphere?
Answer:
The lateral surface area of hemisphere is another name for the curved surface area of hemisphere and the formula for curved surface area of a hemisphere is 2πr2.
Question 2: How to find the base area of a hemisphere?
Answer:
The base area of hemisphere has circular shape and therefore, the area of circle will be used to find the base area of hemisphere. Hence, base area becomes πr2.
Question 3: How to find the surface area of a hemisphere?
Answer:
The formula for total surface area of a hemisphere when the given radius is “r” is 3πr2. Below are the steps provided to find curved surface area of a hemisphere:
- Note down the radius of the hemisphere.
- Put the “r” value in the formula for total surface area of sphere, that is, TSA = 3πr2.
- Present the final answer in square units.
Question 4: Explain the difference between the curved surface area of hemisphere and the surface area of a hemisphere.
Answer:
The curved surface area of hemisphere is only the area covered by the curved surface and the formula for curved surface area of hemisphere is 2πr2. While the surface area of a hemisphere is the sum of the curved surface area and the base area of hemisphere, therefore, the formula for TSA becomes 3πr2.
Question 5: What is the surface area of a hemispherical shell?
Answer:
The surface area of a hemisphere shell is equal to the surface area of a solid hemisphere as we are looking at the surface of the hemisphere and not volume. Therefore, the surface area of the hemispherical shell is 3πr2.
Related Articles
- Surface Area of a Sphere
- Surface Area of a Cube
- Surface Area of a Cuboid
Skip to content
Сфера
Сфера (от греч. «сфайра» — «шар», «мяч») — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки в центре сферы.
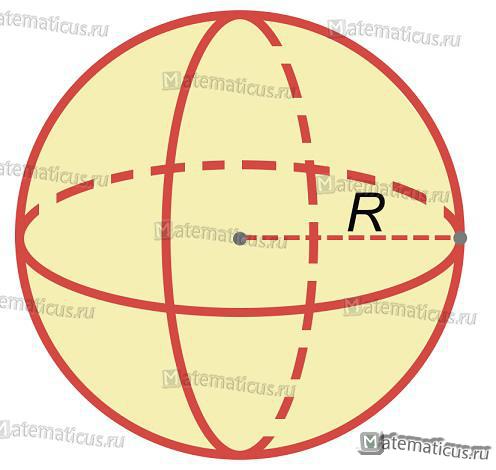
Шар — это тело, ограниченное сферой.
Радиус сферы — отрезок, соединяющий центр и любую точку сферы.
Получить сферу можно вращением полуокружности вокруг ее диаметра.
Секущая плоскость делит сферу на два шаровых сегмента.
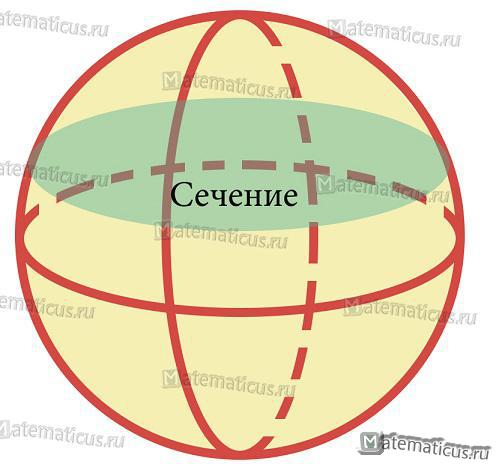
Любое сечение шара или сферы плоскостью есть круг или окружность.
R – радиус сферы или шара;
Формула объёма сферы:
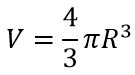
Формула площади сферы (поверхности шара):
S=4πR2
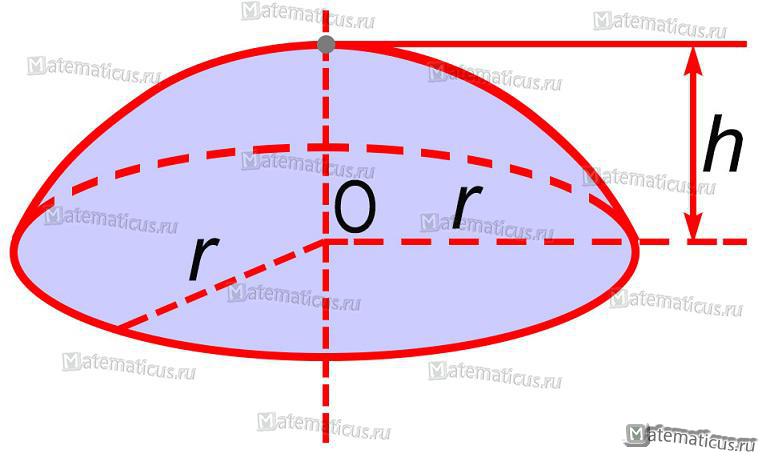
Полусфера
Формула объёма полусферы:
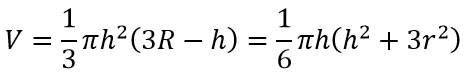
Формула площади полусферы:
S= 2πRh = π(r2+h2)
S= 2πR2
Расчет площади полусферы онлайн.
См. также
Шаровой сегмент, шаровой сектор и шаровой слой
7753
МАТЕМАТИКА
Калькулятор для Общая площадь поверхности полусферы
Этот калькулятор поможет вам найти площадь поверхности формы полусфера. Формула, используемая в этом калькуляторе, приведена ниже.
Чтобы использовать этот калькулятор, вам нужно знать радиус.
CALCULATOR.RESULTS.HEADER
Площадь Поверхности = 942.478
Формула Полусфера Площадь Поверхности
Объяснение переменной формулы:
- H представляет площадь поверхности.
- r представляет Радиус.
Формула LaTeX
Если вы работаете в редакторе на основе TeX, вы можете использовать эту формулу TeX для вычисления полусфера площадь поверхности.
mathrm{H}:=3cdotpicdot{ r}^{2}
Как Рассчитать Полусфера Площадь Поверхности Для Себя
Расчет площадь поверхности довольно просто, если знать приведенную выше формулу. Выполните следующие действия:
-
Затем измените следующие переменные своими значениями:
- r следует заменить на Радиус вашего полусфера. Например, r можно изменить на 10.
- Теперь вы можете ввести это в калькулятор и получить ответ.
|
Найдите площадь поверхности полусферы, диаметр которой равен 2 корня из 3 дм. Какая формула? По какой формуле решать задачу? Какой ответ? Подробное решение. Решение с пояснениями.
Да так же, как и у сферы. Вся разница только в том, что у полусферы площадь будет половина от полной сферы. У вас же половина сферы. Разделите пополам.
rodleoil2 5 месяцев назад Детская задачка-то. Ищите 2 корня из 3 дм Делите пополам найденный диаметр и получаете радиус R S = 4πR^2, где R – радиус искомой сферы, а π – число пи(3.14159 и т.д.). Найденную площадь сферы разделите на 2. Знаете ответ? |
Смотрите также: Что такое равновеликие фигуры (куб, квадрат, многоугольник)? Для чего нужна математика, геометрия, физика в программировании? Как найти вписанный угол ACB, если дуга BC составляет 80 градусов? Как найти длину отрезка BD, если SO = 35, SD = 37? Как найти величину угла OAB, если угол OCD равен 30 градусам? По каким учебникам изучают математику израильские школьники? Как решить: В четырехугольнике АВСD противоположные стороны не параллельны? Диагональ АС параллелограмма АВСD 21, от верш. В до диаг. 12. Чему равна S? Как найти площадь треугольника ABM (см.)? В угол с вершиной D вписана окружность с центром O, которая касается…? |
Сфера, полусфера
Сфера
Сфера (от греч. «сфайра» — «шар», «мяч») — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки в центре сферы.
Шар — это тело, ограниченное сферой.
Радиус сферы — отрезок, соединяющий центр и любую точку сферы.
Получить сферу можно вращением полуокружности вокруг ее диаметра.
Секущая плоскость делит сферу на два шаровых сегмента.
Любое сечение шара или сферы плоскостью есть круг или окружность.
R – радиус сферы или шара;
Формула объёма сферы:
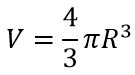
Формула площади сферы (поверхности шара):
S=4 π R 2
Полусфера
Формула объёма полусферы:
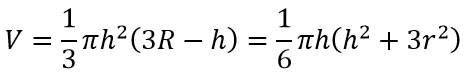
Формула площади полусферы:
S= 2 π Rh = π (r 2 +h 2 )
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.8 / 5. Количество оценок: 5
Сегмент шара
Вычисление площади поверхности и объема шарового сегмента или шарового слоя.
Сегмент шара
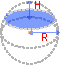Сферический сегмент
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема
Формулы площади поверхности геометрических фигур
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» – это постоянное число, равное отношению длины окружности к её диаметру. В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
- Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.
- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Введите радиус сферы:
Сфера – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Площадь поверхности сферы формула:
S = 4 π R 2 , где R – радиус сферы, π – число пи
Через диаметр
Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
S = 4 π (d/2) 2
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
[spoiler title=”источники:”]
http://planetcalc.ru/283/
http://exceltut.ru/formuly-ploshhadi-poverhnosti-geometricheskih-figur/
[/spoiler]
