Как найти площадь поверхности полушара

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,657
гуманитарные
33,653
юридические
17,917
школьный раздел
611,952
разное
16,904

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Знаток

(254),
закрыт

13 лет назад

Философ

Мыслитель

(9881)

13 лет назад

Поверхность полушара (объемное тело, например, половина арбуза) состоит из двух поверхностей: половины поверхности шара (выпуклая часть) и площади круга ( плоская часть) . Площадь выпуклой части S1 = 2пR (в кв. ) . Площадь плоской части – это площадь круга того же радиуса S2 = пR (в кв. ). Полная поверхность этого объемного тела равна
S = S1 + S2 S = 2пR ( в кв. ) + пR (в кв. ) = 3 пR ( в кв )

Источник: арбуз купил и посмотрел

Источник

1.V= 4/3 πR³=32π/3
4πR³=32π
R³=8 ⇒ R=2
2. Найдем площадь поверхности всего шара
S=4πR²= 16π
Тогда площадь поверхности полушара = 8π.

Комментариев (0)

Ваш ответ

Источник

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) – это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) – это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара:

V =	4	πR³ =	1	πD³
3	6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

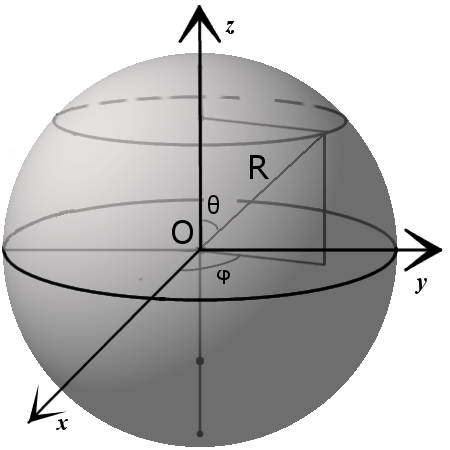
Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x – x₀)² + (y – y₀)² + (z – z₀)² = R²

3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):

x = x₀ + R · sin θ · cos φ
y = y₀ + R · sin θ · sin φ
z = z₀ + R · cos θ

где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

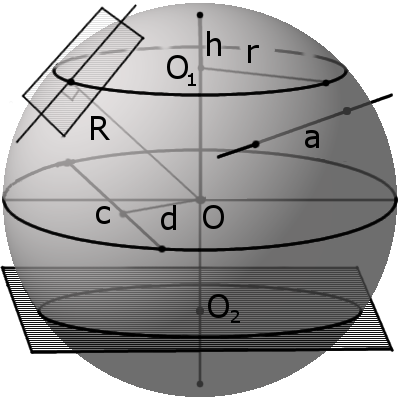
Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы – это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) – это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость – это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость – это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² – m²,

где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.

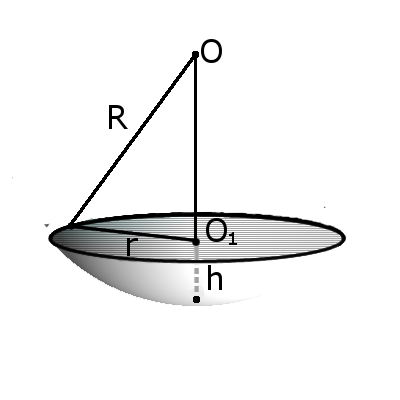
Определение. Полусфера (полушар) – это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере – это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере – это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

Определение. Срез шара – это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.

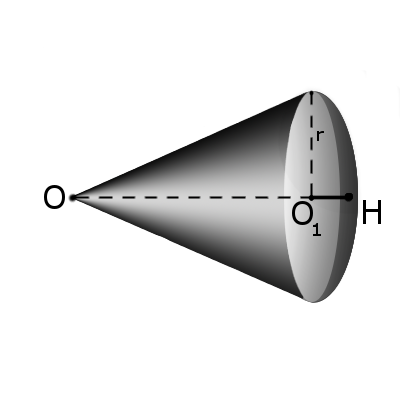
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR – h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Источник

The surface area of a hemisphere is the area covered by the faces of the hemisphere. The curved surface area and the base area sum up to make the total surface area of the hemisphere. The area of only the curved part is called the curved surface area of hemisphere. Before learning the formula for the surface area of hemisphere, let’s understand what is hemisphere followed by the formula and solved examples.

What is the Surface Area of a Hemisphere?

The surface area of a hemisphere is also known as the total surface area of hemisphere. The total surface area of a hemisphere is the total area of all the faces (curved and base area). A hemisphere is formed when a plane divides a sphere into two equal parts. To put it another way, a hemisphere is an exact half of a sphere in geometry. It is made up of two parts: hemi, which means half, and sphere, which is a 3D mathematical shape. When a sphere is sliced at the precise center along its diameter, two equal hemispheres are generated. As a result, a hemisphere is a three-dimensional geometric object consisting of half of a sphere with one side flat and the other as a round bowl.

Surface Area of a Hemisphere Formula

The surface area of a hemisphere is the total surface area of a hemisphere. The surface area of hemisphere is defined by two types of hemispheres, the solid hemisphere, and the hollow hemisphere. The surface area can be found in two ways:

The curved surface area of a hemisphere (CSA).
The total surface area of a hemisphere (TSA).

Curved Surface Area of Hemisphere Formula

The curved surface area of hemisphere formula is defined as the area covered by its curved surface. It is equal to half of the total surface area of a sphere. The formula for the curved surface area of hemisphere equals two times the product of pi and the square of the radius of the hemisphere.

Curved surface area of a hemisphere = 1/2 (Curved surface area of a sphere)

CSA = 1/2 (4πr²)

CSA = 2πr²

Therefore, the formula for curved surface area of hemisphere formula becomes,

CSA = 2πr²

Where,

CSA is the curved surface area,

π is a constant with the value of 3.14,

r is the radius of hemisphere.

Base Area

The base of the hemisphere is in a circular shape, and therefore, the formula for the base area of the hemisphere is equal to the area of a circle.

Base Area = πr²

Total Surface Area of a Hemisphere Formula

The total surface area of a hemisphere is defined as the total space covered by the surface of the hemisphere. The total surface area is given by the sum of its curved surface area and base area. The formula for total surface area equals three times the product of the pi (π) and the square of the radius of the hemisphere.

Total surface area of a hemisphere = Curved surface area + Base area

TSA = 2πr² + πr²

TSA = 3πr²

Therefore, the formula for the total surface area of a hemisphere becomes,

TSA = 3πr²

Where,

TSA is the total surface area,

π is a constant with the value of 3.14,

r is the radius of hemisphere.

Surface Area of a Hollow Hemisphere Formula

The surface area of a hollow hemisphere formula should be first explained in order to understand the formula well. A hollow hemisphere has two diameters as the hollow inner hemisphere creates another smaller diameter. If noted carefully, it can be seen that the surface area of a hollow hemisphere consists of the curved surface area of the bigger hemisphere, the curved surface area of the smaller hemisphere, and the area of the remaining base. Let’s break down the areas in order to obtain the surface area of a hollow hemisphere,

The curved surface area of the outer hemisphere = 2πR²
The curved surface area of the inner hemisphere = 2πr²
The base area of the hollow hemisphere = π(R² – r²)

Therefore, the total surface area of the hemisphere = 2πR² + 2πr²+ π(R² – r²)

TSA = 2πR² + 2πr² + πR² – πr²

TSA = 3πR² + πr²

How to Find the Surface Area of a Hemisphere?

The surface area of a hemisphere can be found by following easy steps based on what type of hemisphere is given. If a solid hemisphere is given, the formula of total surface area and curved surface area can be used based on the requirement, and if a hollow hemisphere is given, the formula for a hollow hemisphere must be used. Following are the steps that can be followed to obtain the surface areas based on the requirement.

Curved Surface Area of a Hemisphere

The formula for the curved surface area of a hemisphere when the given radius is “r” is 2πr². Below are the steps provided to find the curved surface area of a hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the curved surface area of sphere, that is, CSA = 2πr².
Present the final answer in square units.

Example: Calculate the curved surface area of a hemisphere radius of 5 m. (Use π = 3.14).

Solution:

We have,

r = 5

Using the formula we get,

CSA = 2πr²

= 3 (3.14) (5)²

= 235.5 sq. m

Total Surface Area of a Hemisphere

The formula for the total surface area of a hemisphere when the given radius is “r” is 3πr². Below are the steps provided to find the curved surface area of a hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the total surface area of sphere, that is, TSA = 3πr².
Present the final answer in square units.

Example: Calculate the total surface area of a hemisphere diameter of 16cm.

Solution:

We have,

d = 16cm

r = 8cm

Using the formula we get,

TSA = 3πr²

= 3 (3.14) (8)²

= 602.88 sq. cm.

Surface Area of a Hollow Hemisphere

The formula for the surface area of a hollow hemisphere when the given radius is “r” is 3πR²+ πr². Below are the steps provided to find the surface area of a hollow hemisphere:

Note down the radius of the hemisphere.
Put the “r” value in the formula for the total surface area of a sphere, that is, TSA = 3πR²+ πr².
Present the final answer in square units.

Real-Life Examples of Hemisphere

The examples of hemispheres can be seen in everyday life. For instance, the bowl that we use to eat food from is nothing but a hollow hemisphere. The half-cut shell of the coconut is an example of a hollow hemisphere. When we cut round-shaped fruits like oranges, tamarind, watermelon, etc., the shape of the fruit becomes a solid hemispherical shape. Below shown images are real-life examples of hemispheres.

Solved Example on Surface Area of Hemisphere

Example 1: Calculate the total surface area of a hemisphere radius of 4 m.

Solution:

We have,

r = 4

Using the formula we get,

TSA = 3πr²

= 3 (3.14) (4)²

= 150.72 sq. m

Example 2: Calculate the radius of a hemisphere if its total surface area is 200 sq. m.

Solution:

We have,

A = 200

Using the formula we get,

A = 3πr²

=> r² = A/3π

=> r² = 200/3 (3.14)

=> r = 4.60 m

Example 3: Calculate the radius of a hemisphere if its total surface area is 350 sq. m.

Solution:

We have,

A = 200

Using the formula we get,

A = 3πr²

=> r² = A/3π

=> r² = 350/3 (3.14)

=> r = 6.09 m

Example 4: Calculate the curved surface area of a hemisphere radius of 4 m.

Solution:

We have,

r = 4

Using the formula we get,

CSA = 2πr²

= 3 (3.14) (4)²

= 150.72 sq. m

Example 5: Calculate the radius of a hemisphere if its curved surface area is 790 sq. m.

Solution:

We have,

A = 790

Using the formula we get,

A = 2πr²

=> r² = A/2π

=> r² = 350/2 (3.14)

=> r = 7.46 m

FAQs on Surface Area of a Hemisphere

Question 1: What is the lateral surface area of a hemisphere?

Answer:

The lateral surface area of hemisphere is another name for the curved surface area of hemisphere and the formula for curved surface area of a hemisphere is 2πr².

Question 2: How to find the base area of a hemisphere?

Answer:

The base area of hemisphere has circular shape and therefore, the area of circle will be used to find the base area of hemisphere. Hence, base area becomes πr².

Question 3: How to find the surface area of a hemisphere?

Answer:

The formula for total surface area of a hemisphere when the given radius is “r” is 3πr². Below are the steps provided to find curved surface area of a hemisphere:

Note down the radius of the hemisphere.

Put the “r” value in the formula for total surface area of sphere, that is, TSA = 3πr².

Present the final answer in square units.

Question 4: Explain the difference between the curved surface area of hemisphere and the surface area of a hemisphere.

Answer:

The curved surface area of hemisphere is only the area covered by the curved surface and the formula for curved surface area of hemisphere is 2πr². While the surface area of a hemisphere is the sum of the curved surface area and the base area of hemisphere, therefore, the formula for TSA becomes 3πr².

Question 5: What is the surface area of a hemispherical shell?

Answer:

The surface area of a hemisphere shell is equal to the surface area of a solid hemisphere as we are looking at the surface of the hemisphere and not volume. Therefore, the surface area of the hemispherical shell is 3πr².

Surface Area of a Sphere

Surface Area of a Cube

Surface Area of a Cuboid

Источник