Как найти площадь поверхности правильной шестиугольной пирамиды

Как найти площадь поверхности правильной шестиугольной пирамиды

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

  • Формула площади правильной пирамиды

    • 1. Общая формула

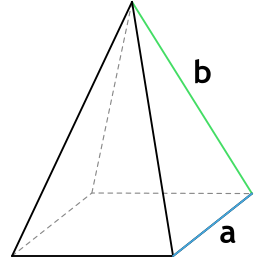
    • 2. Площадь правильной треугольной пирамиды

    • 3. Площадь правильной четырехугольной пирамиды

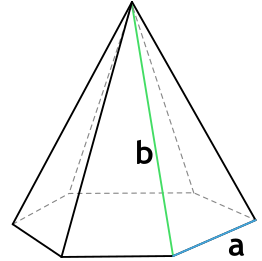
    • 4. Площадь правильной шестиугольной пирамиды

Формула площади правильной пирамиды

Формула площади поверхности правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Sполн. = Sбок. + Sосн.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Нахождение площади правильной пирамиды: формулы

Площадь треугольника вычисляется по формулам:

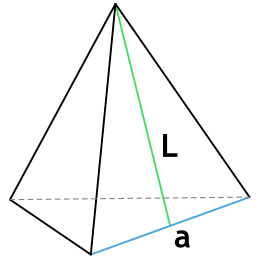
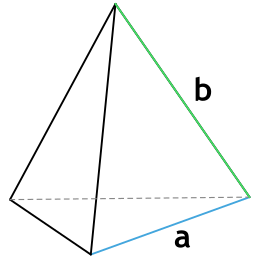
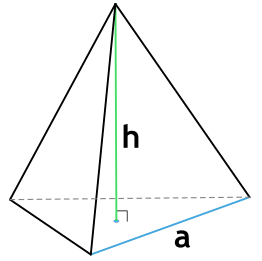
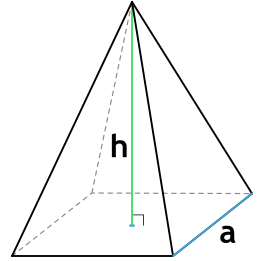
1. Через длину основания (a) и высоту (h):

Формула площади треугольника

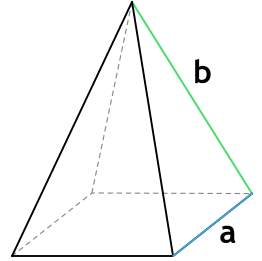
2. Через основание (a) и боковую сторону (b):

Формула площади равнобедренного треугольника

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

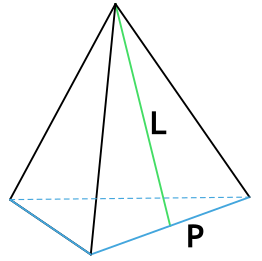
2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

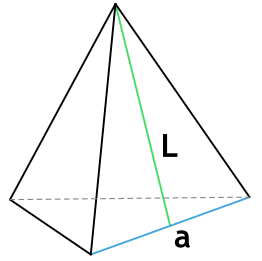
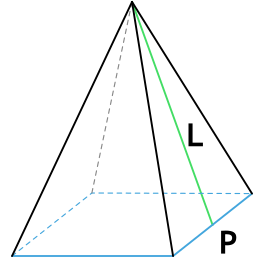
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.

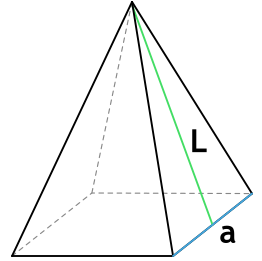
3. Площадь правильной четырехугольной пирамиды

Площадь правильной четырехугольной пирамиды

Основание: квадрат.
Площадь Формула
основание Sосн. = a2
боковая поверхность Sбок. = 2aL
Нахождение площади правильной пирамиды: формулы
полная Sполн. = a2 + 2aL
Нахождение площади правильной пирамиды: формулы

microexcel.ru

4. Площадь правильной шестиугольной пирамиды

Площадь поверхности правильной шестиугольной пирамиды

Основание: правильный шестиугольник

Источник

Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной.
шестиугольная пирамид
Этот многогранник отличается множеством свойств:

  • Все стороны и углы основания равны между собой;
  • Все ребра и двугранные угля пирамиды также равны между собой;
  • Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.

Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:

S_bok={1/2}Pa

где P – периметр основания, a – длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете площади треугольной пирамиды.Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.

Иконка карандаша 24x24Пусть дана правильная шестиугольная пирамида, в которой апофема равна a = 7 см, сторона основания b = 3 см. Рассчитайте площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле: P=6*b
Подставляем данные в формулу: P=6*3=18 cm
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:
S_bok={1/2}*18*7=9*7=63{cm}^2

Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
S_osn={3sqrt{3}}/2*b^2

Иконка карандаша 24x24Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условия из прошлого примера.Из них мы знаем, что сторона основания b = 3 см. Подставим данные в формулу:
S_osn={3sqrt{3}}/{2*3^2}={3sqrt{3}*9}/2=4,5*3sqrt{3}=22,95{cm}^2

Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:
S_poln=S_osn+S_bok

Рассмотрим пример расчета площади шестиугольной пирамиды.

Иконка карандаша 24x24Пусть дана пирамида, в основании которой лежит правильный шестиугольник со стороной b = 4 см. Апофема заданного многогранника равна a = 6 см. Найдите полную площадь.
Мы знаем, что полная площадь состоит из площадей основания и боковой развертки. Поэтому для начала найдем их. Рассчитаем периметр:
P=6*4=24 cm
Теперь найдем площадь боковой поверхности:
S_bok={1/2}*24*6=12*6=72{cm}^2
Далее рассчитываем площадь основания, в котором лежит правильный шестиугольник:
S_osn={3sqrt{3}}/{2*4^2}={3sqrt{3}*16}/2=3sqrt{3}*8=40,8{cm}^2
Теперь можем сложить получившиеся результаты:
S_poln=40,8+72=112,8{cm}^2

Источник

Площадь поверхности правильной пирамиды через периметр, площадь и апофему

{S_{полн} = dfrac{1}{2}PL + S}

На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.

  1. калькулятор площади поверхности пирамиды
  2. формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
  3. формула площади полной поверхности правильной пирамиды через сторону основания и высоту
  4. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
  5. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
  6. формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
  7. формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
  8. формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
  9. формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
  10. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
  11. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
  12. формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
  13. формула площади боковой поверхности правильной пирамиды через периметр и апофему
  14. формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
  15. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
  16. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
  17. формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
  18. формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
  19. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
  20. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
  21. формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
  22. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
  23. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
  24. формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
  25. примеры задач

Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

Площадь полной поверхности пирамиды – это сумма площадей боковых граней и площади основания.

Площадь боковой поверхности пирамиды – это совокупная площадь всех боковых граней пирамиды.

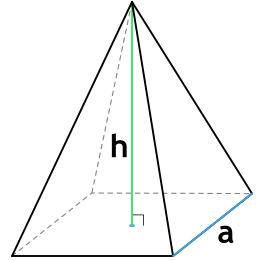
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.

Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему

Площадь полной поверхности правильной пирамиды через периметр, площадь и апофему

{S_{полн} = dfrac{1}{2}PL+S}

P – периметр основания пирамиды

L – апофема пирамиды

S – площадь основания пирамиды

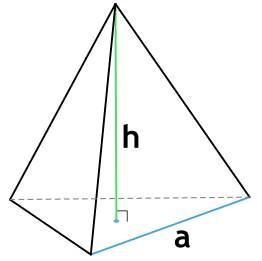
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту

Площадь полной поверхности правильной пирамиды через сторону основания и высоту

{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}

a – сторона основания пирамиды

h – высота пирамиды

n – число сторон основания

Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему

Площадь полной поверхности правильной треугольной пирамиды через сторону основания и апофему

{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}

a – сторона основания пирамиды

L – апофема пирамиды

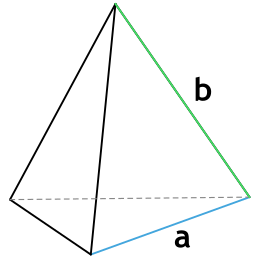
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань

Площадь полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань

{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 – dfrac{a^2}{4}}}{4}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту

Площадь полной поверхности правильной треугольной пирамиды через сторону основания и высоту

{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}

a – сторона основания пирамиды

h – высота пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань

Площадь полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань

{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту

Площадь полной поверхности правильной четырехугольной пирамиды через сторону и высоту

{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}

a – сторона основания пирамиды

h – высота пирамиды

Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему

Площадь полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему

{S_{полн} = a^2+2aL}

a – сторона основания пирамиды

L – апофема пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему

Площадь полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему

{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}

a – сторона основания пирамиды

L – апофема пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

Площадь полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту

Площадь полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту

{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}

a – сторона основания пирамиды

h – высота пирамиды

Формула площади боковой поверхности правильной пирамиды через периметр и апофему

Площадь боковой поверхности правильной пирамиды через периметр и апофему

{S_{бок} = dfrac{1}{2}PL}

P – периметр основания пирамиды

L – апофема пирамиды

Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту

Площадь боковой поверхности правильной пирамиды через сторону основания и высоту

{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }

a – сторона основания пирамиды

h – высота пирамиды

n – число сторон основания

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему

Площадь боковой поверхности правильной треугольной пирамиды через сторону основания и апофему

{S_{бок} = dfrac{3}{2}aL}

a – сторона основания пирамиды

L – апофема пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань

Площадь боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань

{S_{бок} = dfrac{3a sqrt{b^2 – dfrac{a^2}{4}}}{2}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту

Площадь боковой поверхности правильной треугольной пирамиды через сторону основания и высоту

{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}

a – сторона основания пирамиды

h – высота пирамиды

Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему

Площадь боковой поверхности правильной треугольной пирамиды через периметр основания и апофему

{S_{бок} =dfrac{1}{2}PL}

P – периметр основания пирамиды

L – апофема пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему

Площадь боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему

{S_{бок} = 2aL}

a – сторона основания пирамиды

L – апофема пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань

Площадь боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань

{S_{бок} = 2a sqrt{b^2 – dfrac{a^2}{4}}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту

Площадь боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту

{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}

a – сторона основания пирамиды

h – высота пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему

Площадь боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему

{S_{бок} = 3aL}

a – сторона основания пирамиды

L – апофема пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

Площадь боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}

a – сторона основания пирамиды

b – боковая грань пирамиды

Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту

Площадь боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту

{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}

a – сторона основания пирамиды

h – высота пирамиды

Примеры задач на нахождение площади поверхности пирамиды

Задача 1

Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.

Решение

Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.

S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 – 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²

Ответ: 12240 см²

Проверим полученный ответ с помощью калькулятора .

Задача 2

Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.

Решение

Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.

S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²

Ответ: 90 см²

Убедимся в правильности решения с помощью калькулятора .

Задача 2

Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.

Решение

Подставим значения в формулу и произведем расчет.

S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²

Ответ: 60 см²

Проверка .

Источник


Download Article


Download Article

The surface area of any pyramid can be found by adding the surface area of the base to the surface area of the lateral faces. When working with regular pyramids, you can find the surface area using a formula, as long as you know how to find the area of the base of the pyramid. Since the base can be any polygon, it is helpful to know how to find the area of shapes such as pentagons and hexagons. When working with the common, regular square pyramid, however, calculating the total surface area is a simple calculation, provided you know the slant height of the pyramid and the side length of the square base.

  1. Image titled Find the Surface Area of a Pyramid Step 1

    1

  2. Image titled Find the Surface Area of a Pyramid Step 2

    2

    Plug the perimeter of the base into the formula. If you aren’t given the perimeter but know the length of one edge of the base, you can calculate the perimeter by multiplying the length of one edge by the number of edges.

    Advertisement

  3. Image titled Find the Surface Area of a Pyramid Step 3

    3

    Plug the value of the slant height into the formula. Make sure you are using the slant height, not the perpendicular height. The problem should provide the slant height. If you don’t know the slant height, you cannot use this method.

    • For example, if the slant height of a hexagonal pyramid is 12 cm, your formula will look like this: SA={frac {24times 12}{2}}+B.

  4. Image titled Find the Surface Area of a Pyramid Step 4

    4

    Calculate the area of the base. How you do this will depend on the shape of the base. To learn more about finding the area of a polygon, read Find the Area of Regular Polygons.

    EXPERT TIP

    Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University.

    Grace Imson, MA

    Grace Imson, MA
    Math Instructor, City College of San Francisco

    Our Expert Agrees: The surface area of a pyramid is equal to the sum of the areas of all of the faces. First, you have to get the area of the base, then add the area of the lateral sides, which is one face times the number of sides.

  5. Image titled Find the Surface Area of a Pyramid Step 5

    5

    Plug the area of the base into the formula. Make sure you substitute for the variable B.

    • For example, if the area of the hexagonal base is 41.57 sq. cm., your formula for surface area will now look like this: SA={frac {24times 12}{2}}+41.57.

  6. Image titled Find the Surface Area of a Pyramid Step 6

    6

    Multiply the perimeter of the base and the slant height of the pyramid. Then, divide by two. This will give you the lateral surface area of the pyramid.

  7. Image titled Find the Surface Area of a Pyramid Step 7

    7

    Add the two values together. The sum will be the lateral surface area, plus the base surface area, providing you with the total surface area for the pyramid, in square units.

    8. Advertisement

  1. Image titled Find the Surface Area of a Pyramid Step 8

    1

  2. Image titled Find the Surface Area of a Pyramid Step 9

    2

  3. Image titled Find the Surface Area of a Pyramid Step 10

    3

    Square the side length of the base. This will give you the surface area of the base.

  4. Image titled Find the Surface Area of a Pyramid Step 11

    4

    Multiply the side length of the base by the slant height and divide by two. Then, multiply by 4. This will give you the lateral surface area of the pyramid.

  5. Image titled Find the Surface Area of a Pyramid Step 12

    5

    Add the base surface area and the lateral surface area. This will give you the total surface area of the pyramid, in square units.

    6. Advertisement

Add New Question

  • Question

    How do you find the lateral area of hexagonal pyramid, given the height and length of each side?

    Community Answer

    Use the base times height for the rectangles, and the altitude times base of the hexagonal face times three.

  • Question

    How would you calculate the surface area of pyramid that does not have a square base?

    Community Answer

    Use the formula (p x h/2) + (B), where p is the perimeter of the base, h is the slant height of the pyramid, and B is the area of the base. Below are some articles on finding the area of a pentagon and hexagon, two common pyramid bases:

    http://www.wikihow.com/Find-the-Area-of-a-Pentagon
    http://www.wikihow.com/Calculate-the-Area-of-a-Hexagon

  • Question

    How do I double the lateral surface area of a square pyramid?

    Donagan

    One way would be to double either the length of the sides of the base or the slant height (but not both).

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Things You’ll Need

  • Writing utensil
  • Paper
  • Calculator (optional)
  • Ruler (optional)

About This Article

Article SummaryX

To find the surface area of a pyramid, start by multiplying the perimeter of the pyramid by its slant height. Then, divide that number by 2. Finally, add the number you get to the area of the pyramid’s base to find the surface area. To learn how to find the surface area of a square pyramid, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 387,587 times.

Did this article help you?

Источник

Добавить комментарий