Площадь прямоугольника


4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении.

Опыт работы учителем математики – более 33 лет.
Понятия площади
Любая фигура имеет свою площадь, а вычисление площади отталкиваются от единичного квадрата, то есть от квадрата с длиной стороны в 1 мм, либо 1 см, 1 дм и так далее. Площадь такой фигуры равна $1*1 = 1мм^2$, либо $1см^2$ и т. д. Площадь, как правило, обозначается буквой S.
Площадь показывает размер части плоскости, которую занимает фигура, очерченная отрезками.
Прямоугольником называется четырехугольник, у которого все углы одинаковой градусной меры и равны по 90 градусов, а противоположные стороны попарно параллельны и равны.
Особое внимание нужно обращать на единицы измерения длины и ширины. Они должны совпадать. Если единицы не совпадают, их переводят. Как правило переводят большую единицу в меньшую, например, если длина дается в дм, а ширина в см, то дм переводят в см, а результат получится в $см^2$.
Формула площади прямоугольника
Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.

Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см2. Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина. Таким образом, можно вывести формулу площади прямоугольника:
S = a · b, где a,b – ширина и длина фигуры.
К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.
Расчет площади прямоугольника, с использованием его диагонали
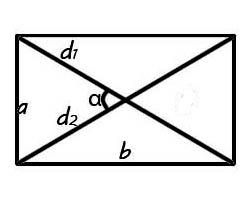
Для того, чтобы рассчитать площадь прямоугольника через диагональ необходимо применить формулу:
$$S = {1over{2}} ⋅ d^2 ⋅ sin{α}$$
Если в задании дано значения угла между диагоналями, а также значение самой диагонали, то можно вычислить площадь прямоугольника по общей формуле произвольных выпуклых четырехугольников.
Диагональ – это отрезок, который соединяет противоположные точки фигуры. Диагонали прямоугольника равны, и точкой пересечения делятся пополам.
Примеры
Для закрепления темы рассмотрим примеры заданий:
№1. Найти площадь огородного участка, такой формы как на рисунку.
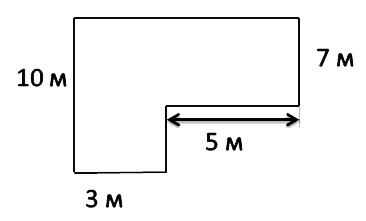
Решение:
Для того чтобы вычесть площадь, необходимо фигуру разбить на два прямоугольника. Один из них будет иметь размеры 10 м и 3 м, другой 5 м. и 7 м. Отдельно находим их площади:
$S_1 =3*10=30 м^2$;
$S_2=5*7=35 м^2$.
Далее необходимо найти их сумму:
$30+35=65 м^2$
Это и будет площадь огородного участка $S = 65 м^2$.
№2. Вычислить площадь прямоугольника, если его диагональ d=6 см. а угол между диагоналями α =300.
Решение:
Значение $sin 30 ={1over{2}} $,
$ S ={1over{2}}⋅ d^2 ⋅ sinα$
$S ={1over{2}} * 6^2 * {1over{2}} =9 см^2$
Таким образом, $S=9 см^2$.
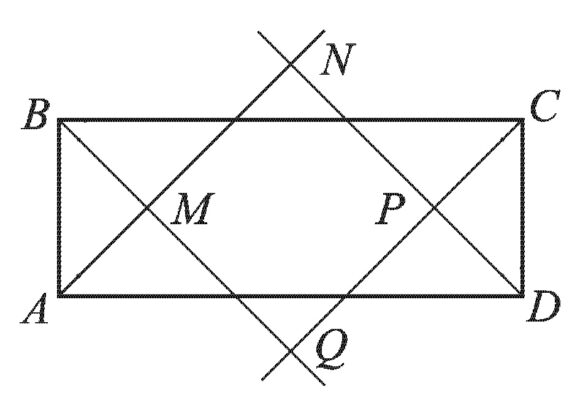
Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Dima Erlichenkov
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
А какая ваша оценка?
Математика
5 класс
Урок №30
Площадь прямоугольника. Единицы площади
Перечень рассматриваемых вопросов:
– понятие площади фигуры;
-единицы измерения площади;
– площадь прямоугольника, квадрата;
– приближенное измерение площади фигуры на клетчатой бумаге.
Тезаурус
Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам).
Квадрат – прямоугольник, у которого все стороны равны.
Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Основная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?
Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.
Для начала введём понятие площади фигуры.
Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см2.
За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.
Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.
Далее покажем, что подразумевается под площадью прямоугольника.
Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Называя величину площади, необходимо указывать единицу измерения.
Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см2. Следовательно, площадь всего прямоугольника равна 15 см2.

S = 15 см2
Решим задачу.
Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.

В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см2 = 6 см · 7 см = АВ · ВС.
Поэтому можно ввести формулу для нахождения площади прямоугольника.
Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.
S = а · b
Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.
S = а · а = а2
Далее найдём соотношение между единицами измерения площадей.
Так как 1 см = 10 мм, следовательно, 1 см2 = 102 мм2 = 100 мм2.
Соответственно, 1 дм2 = 102 см2 = 100 см2
1 м2 = 102 дм2 = 100 дм2
1 км2 = 10002 м2 = 1000000 м2.
Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.
1 ар = 102 м2 = 100 м2
Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.
1 га = 1002 м2 = 10000 м2 = 100 а
Решим задачу.
Найдём площадь прямоугольника.

При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.
S (с недостатком) = 3 · 5 = 15 см2
Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.
S (с избытком) = 4 · 6 = 24 см2
Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.
15 см2 < S < 24 см2
Отметим, что равные прямоугольники имеют равную площадь.
Сравним площади закрашенных квадратов, изображённых на рисунке.

Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.
Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.
Примеры заданий из Тренировочного модуля
№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?
Решение: Для нахождения площади квадрата воспользуемся следующей формулой:
S = а2 = 5см · 5 см = 25 см2
№ 2. Найдите площадь фигуры.

Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см2. Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см2. И вычесть 2 см2 из 30см2.
Ответ: 28 см2.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
-
Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.

{S_{полн} = 2(ab+bc+ac)}
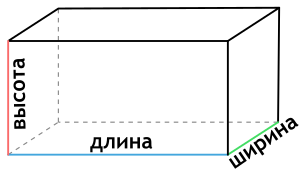
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
