В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
- 1. Через радиус
- 2. Через диаметр
-
Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2

Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!

Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
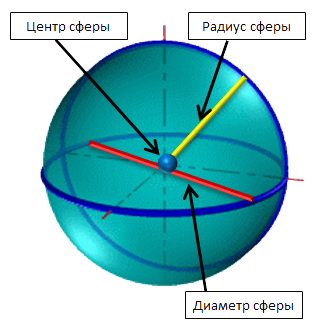
Важно!

Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
![]()
Формула площади сферы:
S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)
Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:
S = 4 · πR2 =
4 · 3 ·
(1 ) 2 =
4 · ·
() 2 =
4 · ·
=
=
= =
=
=
45
м2
Как найти объем шара
Запомните!
![]()
- Формула объема шара:
V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
-
V =
π R3 =π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
-
Вычислите радиус шара, если его объем равен
4 м3 (возьмите π как
3)
Выразим из формулы объема шара радиус.
- V =
π R3 -
π R3
= V -
π R3
=
-
R3
=
Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».
R3
= (3 ·
4) /
(4 · 3)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 ·
4 =
3 ·
=
=
Теперь снова подставим полученное значение в нашу формулу:
-
R3
=
/ (4 · 3)=
/ (4 · )
=
/ () =
=
· () =
= =
=
= 1
- R3 = 1
- R = 1 м
Важно!

Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2019 в 22:59
Руслан Магомедов

Профиль
Благодарили: 0
Сообщений: 1

Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с
0
Спасибо
Ответить
Обратите внимание на предметы, изображенные на рисунке:
Эта информация доступна зарегистрированным пользователям
Давайте подумаем, что же их может объединять?
Очевидно, что цвет и фактура у этих объектов различна, но если вы обратите внимание на форму, то заметите явное сходство.
В математике (геометрии) важную роль при описании и представлении тела играет его геометрическая форма.
Все представленные объекты на рисунке объемные тела (т.е. их в реальности можно посмотреть и потрогать со всех сторон).
Отметим еще одну важную общую черту: у всех изображенных объектов отсутствуют углы (т.е. в действительности они шарообразной, или еще называют: сферической формы, их свободно можно покатать в любые стороны).
Давайте же разберемся, что такое шар, а что называют сферой.
Определим, какими элементами описывают данные геометрические фигуры, какими они свойствами обладают.
Узнаем, как определить площадь сферы, объем круга и рассмотрим примеры решения задач.
Шар – это множество точек пространства, равноудаленных от некоторой заданной точки – центра шара.
Сфера – это поверхность шара (оболочка). Сфера внутри полая.
Примеры сфер: мыльный пузырь, мяч, глобус. Эти тела состоят из оболочки, но внутри пустые.
Можно сказать, что шар – это геометрическое тело, ограниченное сферой (шаровой поверхностью).
Шар внутри заполнен.
Примеры шаров: арбуз, пушечное ядро, бильярдный шар. Эти тела заполненные внутри.
Центр шара (сферы) – это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки, находящейся на шаровой поверхности.
Центр шара (сферы) обозначают обычно заглавной буквой О.
Сфера и шар пространственные фигуры, но определяются такими же элементами, что и окружность, и круг на плоскости.
Радиус шара– это отрезок, соединяющий точку поверхности шара (шаровой поверхности) с его центром.
Радиус обозначается строчной латинской буквой r или заглавной R.
Для шара можно провести столько же радиусов, сколько точек имеет поверхность шара, при этом все эти радиусы равны.
Диаметром шара называют отрезок, проходящий через центр шара и соединяющий две точки шаровой поверхности.
Обычно диаметр обозначают строчной латинской буквой d или заглавной D.
По величине диаметр равен двум радиусам, лежащим на одной прямой.
d = 2r
Следовательно, радиус – это половина диаметра.
r = d : 2
Точки сферы, являющиеся концами диаметра сферы, называют диаметрально противоположными.
Для сферы характерны те же элементы, которые используют для описания шара.
При построении изображений пространственных (объемных) фигур на листе бумаги или иной плоской поверхности, приходится рисовать рисунок так, чтобы он казался объемным- для этого линии, которые не видны глазу человека, изображают штрихпунктирной линией.
Рассмотрим, как выглядят шар, сфера и элементы, их характеризующие, на плоскости.
Эта информация доступна зарегистрированным пользователям
Сфера и шар- это фигуры вращения.
Подобно секущей прямой для круга, для шара существует секущая плоскость.
Рассмотрим, как могут быть расположены по отношению друг к другу плоскость и шар (сфера) в пространстве:
1. Если расстояние от центра шара (сферы) до плоскости больше длины радиуса шара (сферы), то шар (сфера) и плоскость не имеют ни одной общей точки.
Эта информация доступна зарегистрированным пользователям
На рисунке:
Отрезок ОМ = r – это радиус шара.
Отрезок ОА = m – это расстояние от центра шара (сферы) до плоскости
Для данного случая m > r
2. Если расстояние от центра шара (сферы) до плоскости равно длине радиуса шара (сферы), то шар (сфера) и плоскость имеют единственную общую точку.
Эта информация доступна зарегистрированным пользователям
На рисунке:
Отрезок ОМ = r – это радиус шара.
Отрезок ОА = m – это расстояние от центра шара (сферы) до плоскости
Для данного случая m = r
Точка А общая для плоскости сечения и шара
3. Если расстояние от центра шара (сферы) до плоскости меньше длины радиуса, то плоскость пересекает шар (сферу).
Эта информация доступна зарегистрированным пользователям
На рисунке:
Отрезок ОМ = r – это радиус шара.
Отрезок ОА = m – это расстояние от центра шара (сферы) до плоскости (mathbf{alpha})
Для данного случая m < r
Сечение шара плоскостью представляет круг.
Представить мы можем это на примере апельсина, разрезанного на две части.
Сечением сферы плоскостью является окружность.
Такое сечение мы можем представить, если разрезать теннисный мяч
Эта информация доступна зарегистрированным пользователям
Отсеченная плоскостью часть шара называется шаровым сегментом.
Отсеченную плоскостью часть сферы называют сферическим сегментом.
Если плоскость сечения проходит через центр шара (сферы), то сечением шара (сферы) является самый большой круг (окружность), а радиус круга (окружности) является радиусом самого шара (сферы).
В таком случае шар (сфера) делится на два равных сегмента (две равные части).
Чем дальше проходит секущая плоскость от центра шара (сферы), тем меньше радиус сечения.
Обратите внимание на рисунок:
Эта информация доступна зарегистрированным пользователям
Сечение шара с радиусом сечения r является самым большим кругом, а радиус круга является радиусом самого шара.
Сечение шара с радиусом сечения r1 находится дальше от центра шара, чем сечение шара с радиусом сечения r2 Мы можем заметить на рисунке что r2 > r1
Сечения шара (сферы), удаленные на равные расстояния от центра, имеют равные радиусы:
Эта информация доступна зарегистрированным пользователям
Сечение шара с радиусом сечения r2 и сечение шара с радиусом сечения r3 удаленные на равные расстояния от центра шара, имеют равные радиусы (r2 = r3)
Сфера и шар- фигуры вращения
Шар образуется вращением полукруга около его неподвижного диаметра- оси шара.
Сфера является фигурой вращения, образованной при вращении полуокружности вокруг своего неподвижного диаметра.
АВ– это ось вращения шара (сферы).
Эта информация доступна зарегистрированным пользователям
Если посмотреть вокруг, мы можем заметить множество объектов, имеющих или принимающих форму шара (сферы).
Так, например, падающая микроскопическая капля дождя или капля жидкости, находящаяся в невесомости, принимают форму шара.
Это происходит потому, что давление вокруг жидкости и в самой жидкости примерно равны (т.е. со всех сторон давление на каплю одинаковое), в результате получается шарообразная форма.
Сферической формой обладают мыльные пузыри или пузыри в воде.
Эта информация доступна зарегистрированным пользователям
Происходит это благодаря поверхностному натяжению, свойственному жидкостям (своего рода, «невидимая» оболочка жидкости).
Силы поверхностного натяжения стремятся придать мыльному пузырю оптимальную форму, а этой формой и является шар, так как в шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.
Многие ягоды и фрукты, икринки рыбы, жемчужины и др. в природе являются обладателями шарообразных и сферических форм.
Представления о планетах и небесных телах, молекулах и некоторых элементарных частицах в связи с определенными свойствами и поведением сводятся к модели шара и сферы.
Существует множество примеров использования свойств и характеристик шара (сферы) в науке, технике и производстве.
Эта информация доступна зарегистрированным пользователям
Сферических и шарообразных форм в жизни огромное множество, они прекрасно демонстрируют в своих закономерностях и проявлениях законы физики и математики.
Приводя примеры объектов сферической и шарообразной формы, мы много говорили о площади и объеме этих тел.
Давайте посмотрим, как определить площадь поверхности сферы и объем шара.
Площадь поверхности сферы (площадь поверхности шара) находят по формуле:
(mathbf{S = 4pi r^2})
(mathbf{S = pi d^2})
S– площадь поверхности сферы (шара)
r– радиус сферы (шара)
(mathbf{pi})- постоянная величина, равная приблизительно 3,14
Эта информация доступна зарегистрированным пользователям
Задача 1
Найдите площадь поверхности сферы, радиус которой равен 8 см.
Решение:
Число (mathbf{pi}) округлить до десятых.
Дано:
r = 8 см
(mathbf{pi = 3,1})
Найти:
Площадь поверхности сферы S – ?
Площадь поверхности сферы, зная радиус сферы, определяют по формуле:
(mathbf{S = 4pi r^2})
Подставим известные значения радиуса сферы и постоянной величины (mathbf{pi}), получим
(mathbf{S = 4 cdot 3,1 cdot 8^2 = 793,6}) (см2)
Ответ: S = 793,6 (см2).
Задача 2
Найдите площадь поверхности сферы, диаметр которой равен 6 см.
Решение:
Число (mathbf{pi}) округлить до десятых.
Дано:
d = 6 см
(mathbf{pi = 3,1})
Найти:
Площадь поверхности сферы S – ?
Площадь поверхности сферы, зная диаметр этой сферы, определяют по формуле:
(mathbf{S = pi d^2})
Подставим известные значения радиуса сферы и постоянной величины , получим
(mathbf{S = 3,1cdot 6^2}) (см2)
Ответ: S = 111,6 (см2).
Объем шара определяется по формуле:
(mathbf{V = frac{4}{3}pi r^3})
V– объем шара
r– радиус шара
(mathbf{pi})- постоянная величина, равная приблизительно 3,14
Эта информация доступна зарегистрированным пользователям
Вспомним, что означает r3
(mathbf{r^3 = r cdot r cdot r})
Задача 3
Найдите объем шара, если радиус шара 5 м.
Решение:
Число (mathbf{pi}) округлить до целых.
Дано:
r = 5 м
(mathbf{pi = 3})
Найти:
Объем шара V – ?
Объем шара определяется по формуле:
(mathbf{V = frac{4}{3}pi r^3})
Подставим известные значения радиуса шара и постоянной величины , получим:
(mathbf{V = frac{4}{3}cdot 3 cdot 5^3 = frac{4cdot 3 cdot 5 cdot 5 cdot 5}{3} = 500})(м3) объем шара
Ответ: V = 500 м3
Эта информация доступна зарегистрированным пользователям
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк – лучший сайт для заказа контрольных работ!
Тест по теме «Площадь поверхности шара»
Площадь поверхности шара, или как часто неправильно говорят просто площадь шара, вычисляется по очень простой формуле. Но даже простые вещи можно упростить и именно поэтому мы сделали калькулятор, который в режиме онлайн может рассчитать площадь поверхности шара, а также на странице вы найдете формулу для расчета.
Возможно вам дополнительно потребуется рассчитать и объем шара.
Шар — геометрическое тело, состоящее из точек пространства, которые удалены от центра на расстояние, не более заданного. Это расстояние называют радиусом шара.
Содержание:
- калькулятор площади поверхности шара
- формула площади поверхности шара через радиус
- формула площади поверхности шара через диаметр
- формула площади поверхности шара через длину окружности
- примеры задач
Формула площади поверхности шара через радиус
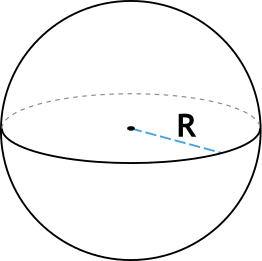
{S = 4pi R^2}
R – радиус шара
Формула площади поверхности шара через диаметр
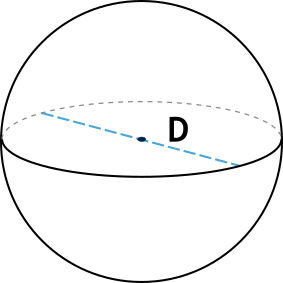
{S = pi D^2}
D – диаметр шара
Формула площади поверхности шара через длину окружности
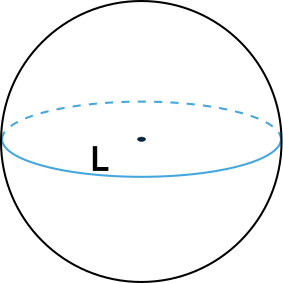
{S = dfrac{L^2}{pi}}
L – длина окружности шара
Примеры задач на нахождение площади поверхности шара
Задача 1
Найдите площадь поверхности шара диаметром 10см.
Решение
Так как в условии дан диаметр шара, мы воспользуемся второй формулой.
S = pi D^2 = pi cdot 10^2 = pi cdot 100 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
калькулятор поможет проверить правильность вычислений.
Задача 2
Найдите площадь поверхности шара, если его радиус равен 5см.
Решение
В этой задаче мы будем использовать первую формулу.
S = 4pi R^2 = 4pi cdot 5^2 = 4pi cdot 25 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
Проверка ответа.
