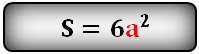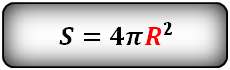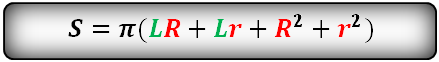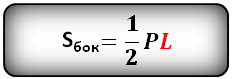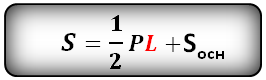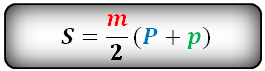Как найти площадь поверхности шара около цилиндра

В данной публикации мы рассмотрим, как найти радиус описанной вокруг прямого цилиндра сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Нахождение радиуса сферы/шара

Около любого цилиндра можно описать сферу (или другими словами, вписать цилиндр в шар) – но только одну.

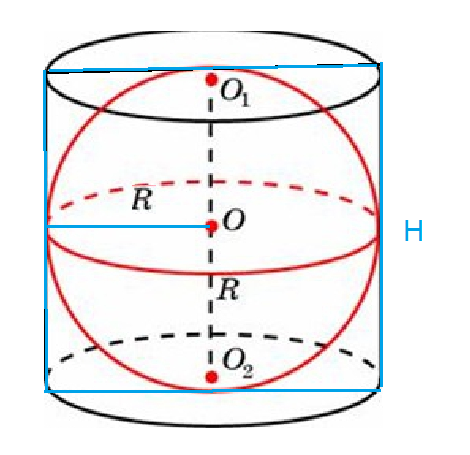
Центром такой сферы будет являться центр цилиндра, в нашем случае – это точка O.
O₁ и O₂ – центры оснований цилиндра.
O₁O₂ – высота цилиндра (h).
OO₁ = OO₂ = ^h/₂.

Можно заметить, что радиус описанной сферы (OE), половина высоты цилиндра (OO₁) и радиус его основания (O₁E) образовывают прямоугольный треугольник OO₁E.

Воспользовавшись теоремой Пифагора мы можем найти гипотенузу этого треугольника, которая одновременно является радиусом сферы, описанной около заданного цилиндра:

Зная радиус сферы можно вычислить площадь (S) ее поверхности и объем (V) ограниченного сферой шара:

S = 4 ⋅ π ⋅ R²
S = ⁴/₃ ⋅ π ⋅ R³

Примечание: π округленно равняется 3,14.

Источник

Решение

Из рисунка, указанного в условии, видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим площадь полной поверхности цилиндра: S _{полн. пов. цил.} = 2S _{осн. цил.} + S _{бок. пов. цил.} = 2pi R^2 + 2pi RH.

2pi R^2 + 2pi RH = 2pi R^2 + 2pi Rcdot 2R = 6pi R^2. По условию 24 = 6pi R^2. Отсюда pi R^2 = 4. Так как S _{пов. шара} = 4pi R^2, то искомая площадь равна 4cdot 4 = 16.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Источник

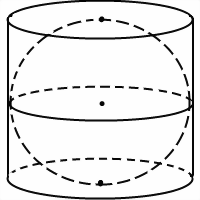
Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).

Если шар вписан в цилиндр, то цилиндр описан около шара.

В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:

R=r.

Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.

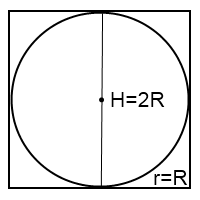
Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:

H=2R

Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара

$[{V_1} = frac{4}{3}pi {R^3}]$

Объем цилиндра

$[{V_2} = pi {r^2}H = pi {R^2} cdot 2R = 2pi {R^3}.]$

Отсюда отношение объема шара к объему описанного около него цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{{frac{4}{3}pi {R^3}}}{{2pi {R^3}}} = frac{2}{3}.]$

Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)

$[{S_1} = 4pi {R^2}]$

Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:

$[{S_2} = {S_{bok}} + 2{S_{ocn}} = 2pi rH + 2pi {r^2} = ]$

$[ = 2pi R cdot 2R + 2pi {R^2} = 6pi {R^2}.]$

Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{4pi {R^2}}}{{6pi {R^2}}} = frac{2}{3}.]$

Источник

Задать свой вопрос

*более 50 000 пользователей получили ответ на «Решим всё»

Задача 51295 Около шара описан цилиндр площадь полной…

Условие

ango2004

2020-05-22 17:18:23

Около шара описан цилиндр площадь полной поверхности которого равна 12 найдите площадь поверхности шара

математика
5719

Решение

sova

2020-05-22 17:21:55

★

Значит, в квадрат вписана окружность

2R=H

S_(полн. цилиндра)=S_(бок)+2S_(осн)=2π*R*H+2π*R^2

Н=2R

=2π*R*(2R)+2π*R^2=6πR^2

По условию

S_(полн. цилиндра)=12

6πR^2=12

[b]πR^2=2[/b]

S_(шара)=4π*R^2=4*([red]π*R^2[/red])=4*2=[b]8[/b]

Написать комментарий

Присоединяйся в ВК

Источник

Все формулы для площадей полной и боковой поверхности тел

1. Площадь полной поверхности куба

a – сторона куба

Формула площади поверхности куба,(S):

2. Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R – радиус сферы

π ≈ 3.14

Формула площади поверхности шара (S):

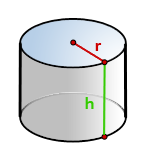
4. Найти площадь боковой и полной поверхности цилиндра

r – радиус основания

h – высота цилиндра

π ≈ 3.14

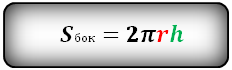
Формула площади боковой поверхности цилиндра, (S_бок):

Формула площади всей поверхности цилиндра, (S):

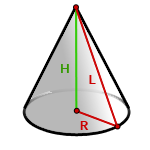
5. Площадь поверхности прямого, кругового конуса

R – радиус основания конуса

H – высота

L – образующая конуса

π ≈ 3.14

Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (S_бок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (S_бок):

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

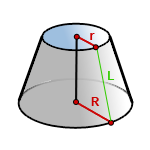
6. Формулы площади поверхности усеченного конуса

R – радиус нижнего основания

r – радиус верхнего основания

L – образующая усеченного конуса

π ≈ 3.14

Формула площади боковой поверхности усеченного конуса, (S_бок):

Формула площади полной поверхности усеченного конуса, (S):

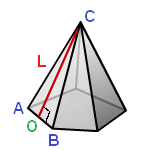
7. Площадь поверхности правильной пирамиды через апофему

L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)

P – периметр основания

S_осн – площадь основания

Формула площади боковой поверхности правильной пирамиды (S_бок):

Формула площади полной поверхности правильной пирамиды (S):

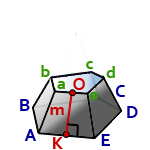
8. Площадь боковой поверхности правильной усеченной пирамиды

m – апофема пирамиды, отрезок OK

P – периметр нижнего основания, ABCDE

p – периметр верхнего основания, abcde

Формула площади боковой поверхности правильной усеченной пирамиды, (S):

9. Площадь поверхности шарового сегмента

R – радиус самого шара

h – высота сегмента

π ≈ 3.14

Формула площади поверхности шарового сегмента, (S):

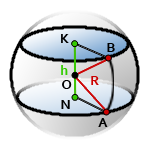
10. Площадь поверхности шарового слоя

h – высота шарового слоя, отрезок KN

R – радиус самого шара

O – центр шара

π ≈ 3.14

Формула площади боковой поверхности шарового слоя, (S):

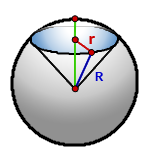
11. Площадь поверхности шарового сектора

R – радиус шара

r – радиус основания конуса = радиус сегмента

π ≈ 3.14

Формула площади поверхности шарового сектора, (S):

Источник

Нахождение радиуса сферы/шара

Решение

Ответ