Как найти площадь поверхности шара зная объем

Как найти площадь поверхности шара зная объем

Alexandr Laketych



Мастер

(1289),
закрыт



3 года назад

Лучший ответ

Александр

Просветленный

(27692)


7 лет назад

Зная объём легко найти радиус. Зная радиус легко найти площадь поверхности шара – то есть площадь сферы:

1) Во втором уравнении вместо V подставь 4pi/3 и найди r.
2) Полученное r подставь в первое уравнение. Найдёшь S – площадь.

Остальные ответы

Похожие вопросы

Источник

Площадь поверхности шара

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Площадь поверхности шара

Чтобы посчитать площадь поверхности шара (площадь сферы) воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Площадь сферы
Чему равна площадь поверхности шара, если:

=

S =

0

Округление числа π: Округление ответа:

Просто введите известный вам параметр, и узнаете площадь сферы шара.

Теория

Ликбез: Поверхность шара — сфера.

Площадь поверхности шара через радиус

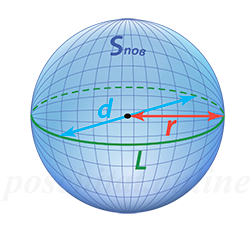
Чему равна площадь поверхности шара Sпов, если его радиус r:

Формула

Sпов = 4⋅π⋅r² , где π ≈ 3.14…

Пример

Для примера посчитаем какая площадь поверхности у шара, если его радиус r = 3 см:

Sпов = 4 ⋅ 3.14 ⋅ 3² = 12.56 ⋅ 9 = 113.04 см²

Площадь поверхности шара через диаметр

Чему равна площадь поверхности шара Sпов, если его диаметр d?

Формула

Sпов = π⋅d² , где π ≈ 3.14…

Пример

Для примера посчитаем какая площадь поверхности у шара, если его диаметр d = 6 см:

Sпов = 3.14 ⋅ 6² = 3.14 ⋅ 36 = 113.04 см²

Площадь поверхности шара через длину окружности

Чему равна площадь поверхности шара Sпов, если длина его окружности L?

Формула

Sпов = L²⁄π , где π ≈ 3.14…

Пример

Для примера посчитаем чему равна площадь поверхности шара, имеющего длину окружности L = 10 см:

Sпов = 10² ⁄ 3.14 ≈ 31.85 см²

См. также

Источник

Статья будет полезна школьникам и будущим абитуриентам, которые готовятся к сдаче ЕГЭ.

Содержание

  • Формула объема шара через радиус: значение
  • Формула объема шара через диаметр: значение
  • Примеры вычисления объема шара, через радиус и диаметр шара: описание
  • Формула полной поверхности шара, сферы через радиус: значение
  • Формула полной поверхности шара, сферы через диаметр: значение
  • Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание
  • Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи
  • Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.

Формула объема шара через радиус: значение

Объем шара V вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.

Данная формула является базовой!

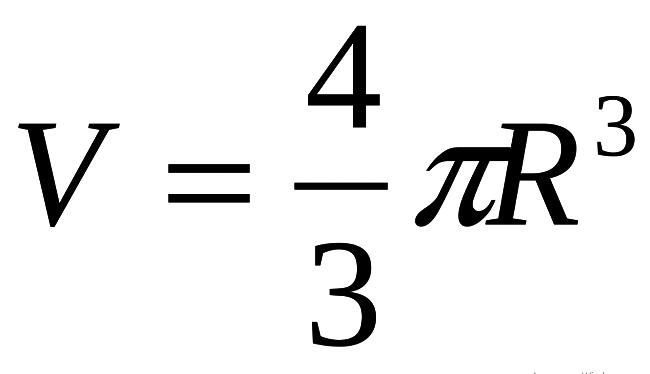
Формула для вычисления объема шара, если известен радиус r шара

Формула для вычисления объема шара, если известен радиус R шара

Формула объема шара через диаметр: значение

  1. Воспользуйтесь базовой формулой: V=4/3*π*R³.
  2. Радиус R — это ½ диаметра D или R=D/2.
  3. Отсюда: V=4/3*π*R³ → V=(4π/3)*(D/2)³ → V=(4π/3)*(D³/8)→ V= πD³/6.

Или

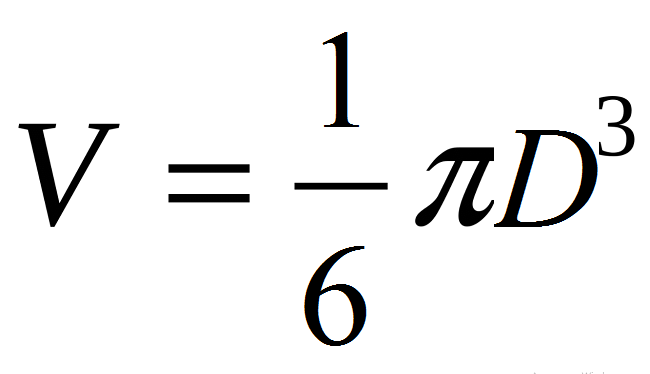
Формула вычисления объема шара, если известен диаметр d шара

Формула вычисления объема шара, если известен диаметр D шара

Примеры вычисления объема шара, через радиус и диаметр шара: описание

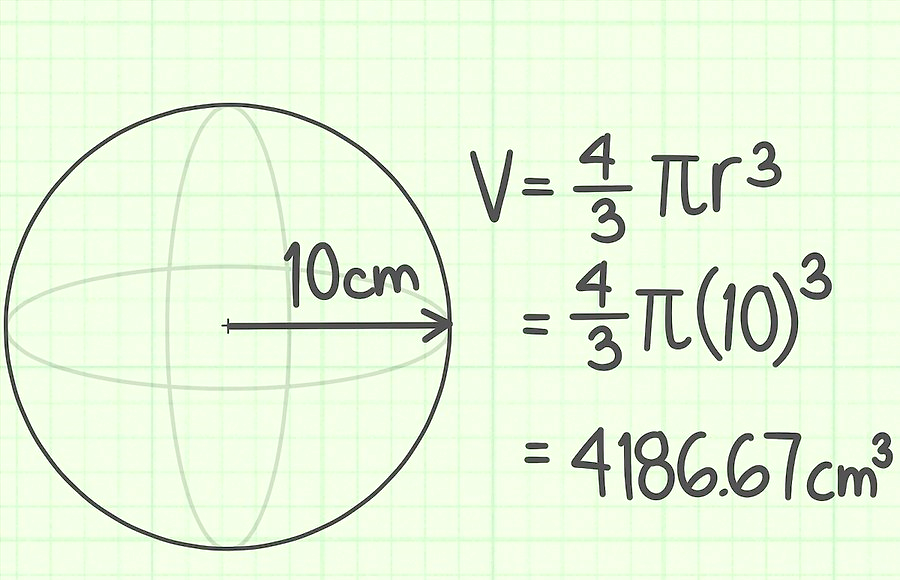
Задача 1.

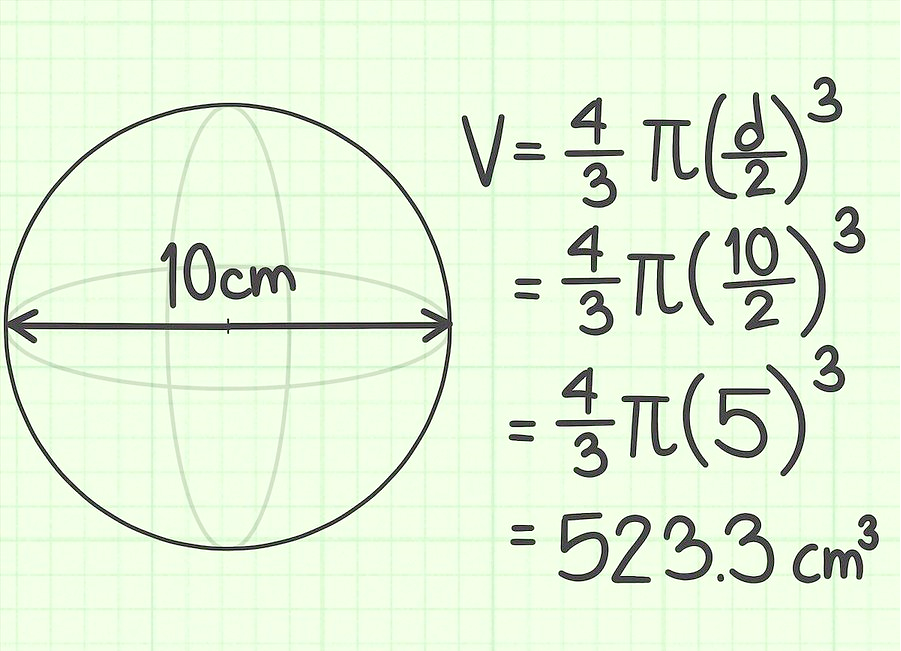
Радиус шара равен 10 см. Найди его объем.

Пример вычисления объема шара, если радиус шара задан в условии задачи

Пример вычисления объема шара, если радиус шара задан в условии задачи

Задача 2.

Диаметр шара равен 10 см. Найди его объем.

Пример вычисления объема шара, если диаметр шара задан в условии задачи

Пример вычисления объема шара, если диаметр шара задан в условии задачи

Задача 3.

Соотношение диаметра Луны и диаметра Земли 1:4. Во сколько раз объем Земли больше объема Луны?

Решение:

Пример решения задачи

Пример решения задачи

Ответ: в 64 раза.

Важно: существует множество онлайн калькуляторов, позволяющих быстро найти заданную величину. Например, сервис Webmath.

Формула полной поверхности шара, сферы через радиус: значение

Площадь поверхности сферы/шара S вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.

Данная формула является базовой!

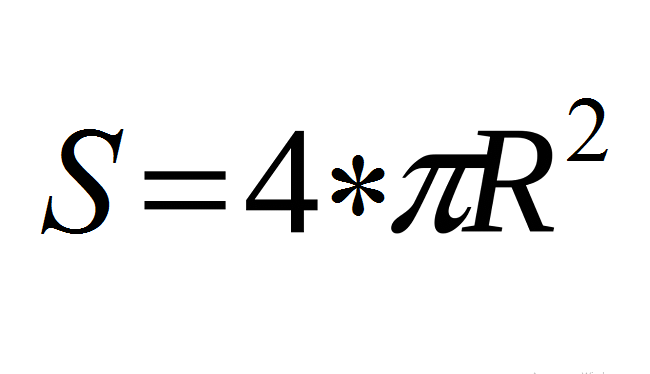
Формула для вычисления площади полной поверхности шара, если известен радиус r шара

Формула для вычисления площади полной поверхности шара, если известен радиус R шара

Формула полной поверхности шара, сферы через диаметр: значение

  1. Воспользуйтесь базовой формулой: S = 4*π*R².
  2. Радиус R — это ½ диаметра D или R=D/2.
  3. Отсюда: S=4*π*R² → S=4*π*(D/2)² → S=(4π)*(D²/4)→ S = (4πD²)/4 → S = πD².

Или

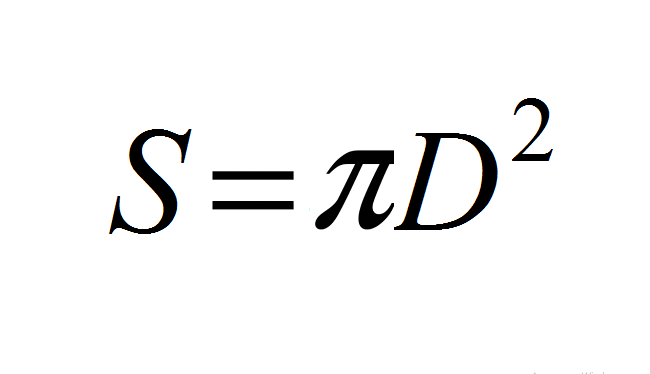
Формула вычисления площади полной поверхности шара, если известен диаметр d шара

Формула вычисления площади полной поверхности шара, если известен диаметр D шара

Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание

Задача 4.

Пример решения задачи

Пример решения задачи

Задача 5.

Пример решения задачи

Пример решения задачи

Задача 6.

Пример решения задачи

Пример решения задачи

Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи

Задача 7.

Пример решения задачи.

Пример решения задачи.

Задача 8.

Пример решения задачи.

Пример решения задачи.

Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.

Источник
Определение шара

Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.

Онлайн-калькулятор площади поверхности шара

поверхность шара

У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.

D=2⋅RD=2cdot R

Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.

Формула площади поверхности шара по радиусу шара

S=4⋅π⋅R2S=4cdotpicdot R^2

RR — радиус шара.

Пример

Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.

Решение

d=300d= sqrt{300}

Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:

d2=a2+a2+a2d^2=a^2+a^2+a^2

d2=3⋅a2d^2=3cdot a^2

a=d3a=frac{d}{sqrt{3}}

a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10

Радиус шара, вписаного в куб равен половине стороны этого куба:

R=a2=102=5R=frac{a}{2}=frac{10}{2}=5

Тогда площадь поверхности шара:

S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)

Ответ: 314 см. кв.

Формула площади поверхности шара по диаметру шара

Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:

S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2

S=π⋅D2S=picdot D^2

DD — диаметр шара.

Пример

Диаметр шара равен 10 (см.). Найдите площадь его поверхности.

Решение

D=10D=10

По формуле получаем:

S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)

Ответ: 314 см. кв.

Студворк – лучший сайт для заказа контрольных работ!

Тест по теме «Площадь поверхности шара»

Источник

В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.

  • Формула вычисления площади шара/сферы

    • 1. Через радиус

    • 2. Через диаметр

  • Примеры задач

Формула вычисления площади шара/сферы

1. Через радиус

Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.

S = 4 π R2

Площадь поверхности шара

Примечание: в расчетах значение числа π округляется до 3,14.

2. Через диаметр

Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:

S = 4 π (d/2)2

Примеры задач

Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.

Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.

Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.

Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Расчет диаметра сферы через площадь ее поверхности

Источник

Добавить комментарий