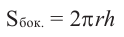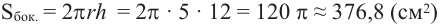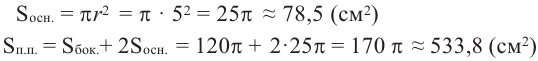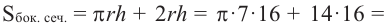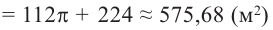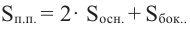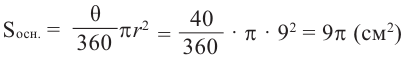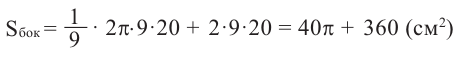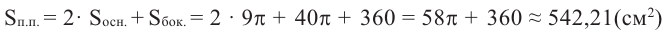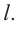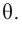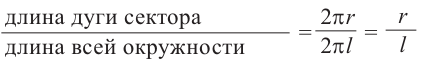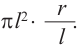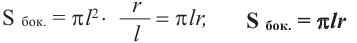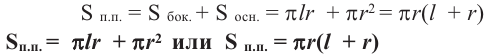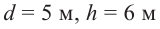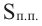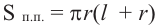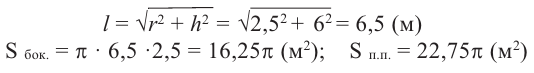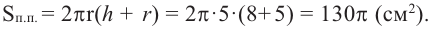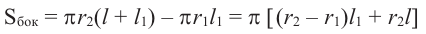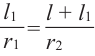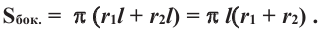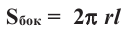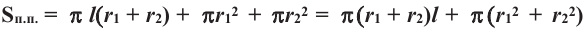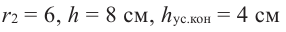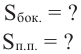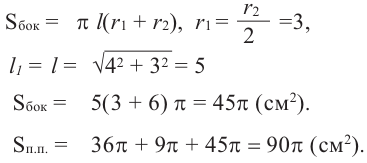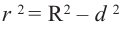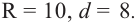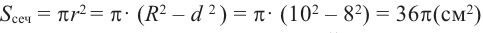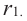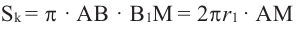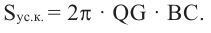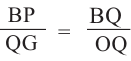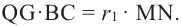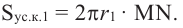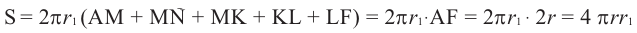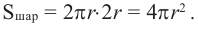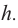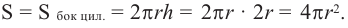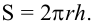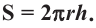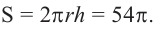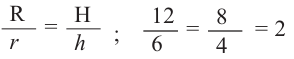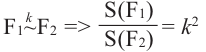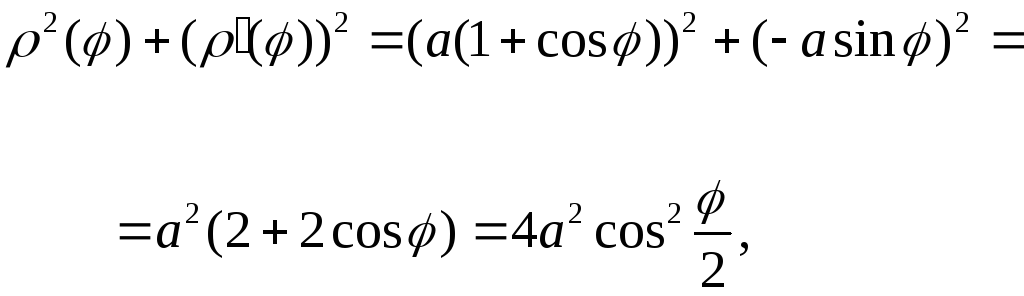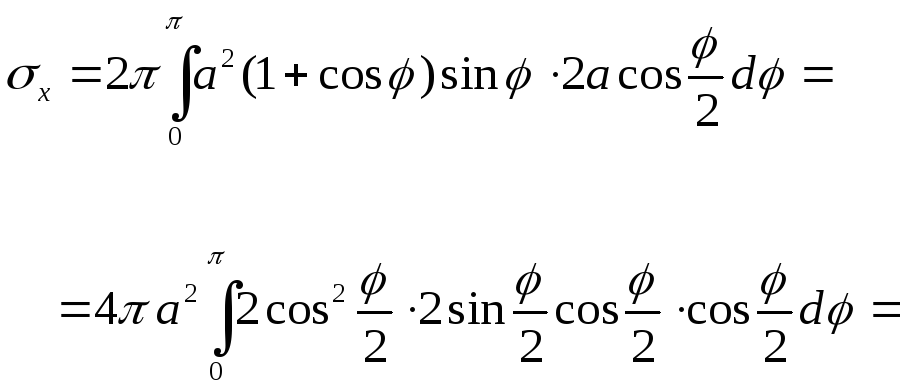Как найти площадь поверхности тела при вращении - Сайт, где вы сможете решить свои вопросы

Онлайн калькулятор для нахождения, вычисления площади поверхности вращения, рисунок тела вращения.
Например, вычислить площадь поверхности тора, полученного вращением окружности x^2+(y-3)^2=1 вокруг оси Ох.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

: Sqrt[x]
: x^(1/n)
$a^{x}$ : a^x
$log_{a}x$ : Log[a, x]
: Log[x]
: cos[x] или Cos[x]

: sin[x] или Sin[x]

: tan[x] или Tan[x]

: cot[x] или Cot[x]

: sec[x] или Sec[x]

: csc[x] или Csc[x]

: ArcCos[x]

: ArcSin[x]

: ArcTan[x]

: ArcCot[x]

: ArcSec[x]

: ArcCsc[x]

: cosh[x] или Cosh[x]

: sinh[x] или Sinh[x]

: tanh[x] или Tanh[x]

: coth[x] или Coth[x]

: sech[x] или Sech[x]

: csch[x] или Csch[е]

: ArcCosh[x]

: ArcSinh[x]

: ArcTanh[x]

: ArcCoth[x]

: ArcSech[x]

: ArcCsch[x]

[19.67] =19: integral part of (19.67) – выделяет целую часть числа (integerPart)

Скачать калькулятор

Рейтинг: 2.3 (Голосов 14)

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Решение определенных интегралов	Решение неопределенных интегралов	Решение двойных интегралов	Решение интегралов
Объем тела вращения	Решение тройных интегралов	Графические построения	Решение задачи Коши

Источник

Содержание:

Великий греческий ученый Архимед был очень взволнован, когда он обнаружил, что отношение площади поверхности шара и описанного около него цилиндра и отношение их объемов равно 2:3. Великий математик, физик, инженер, Архимед, среди всех своих работ самой значимой считал именно эту. Он завещал на своей могильной плите выгравировать доказательство данной теоремы. Из истории известно, что долгое время его родной город Сиракузы, располагающийся на Сицилии, противостоял римлянам именно благодаря оружию, которое изобрел Архимед. Поэтому при взятии города римский военачальники приказал сохранить ученому жизнь. Но римский воин, который не знал Архимеда в лицо, убил его. Великий философ и писатель Цицерон потратил много времени, чтобы отыскать могилу Архимеда (по историческим сведениям он нашел ее через 137 лет). Это дело Цицерона стало идеей для работ многих художников.

Определение фигур вращения

Гончарное ремесло позволяет создавать керамическую посуду из глины. Форму глиняной лепешке придают вращением вокруг оси. Затем полученную форму обжигают. Это ремесло живо и по сей день. В различных районах Азербайджана есть ремесленники, которые изготавливают керамическую посуду. Исследуйте принцип работы по которому кусок глины приобретает какую-либо форму.

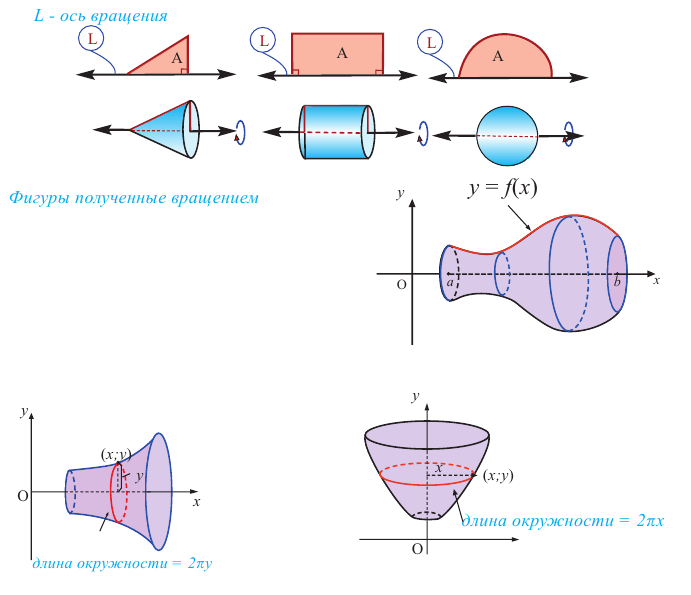
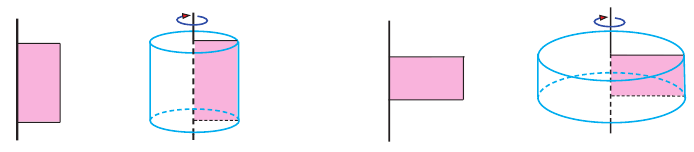
Плоские фигуры (плоская часть ограниченная кривой), совершая один полный оборот вокруг определенной оси, образуют пространственные фигуры. Эта ось называется осью вращении.

Цилиндр, конус и сфера являются простыми пространственными фигурами, полученными при вращении.

Например, при вращении прямоугольного треугольника вокруг одного из катетов получается конус, при вращении прямоугольника вокруг стороны образуется цилиндр, а при вращении полукруга вокруг диаметра – шар.

Цилиндр

Наглядно образование фигур вращения можно увидеть на примере вращающихся стеклянных дверей, которые мы часто видим в общественных зданиях, отелях и больницах. Прямоугольный слой двери, прикрепленный к неподвижной стойке, при вращении очерчивает цилиндр.

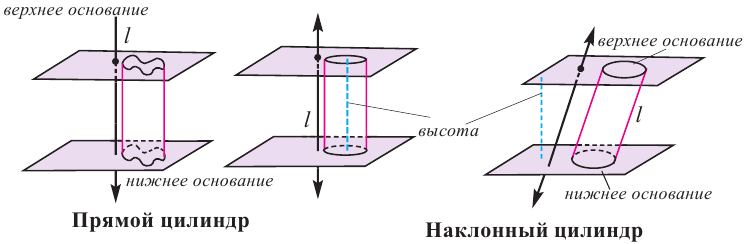
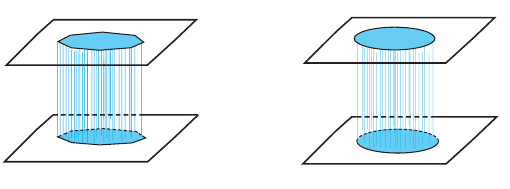
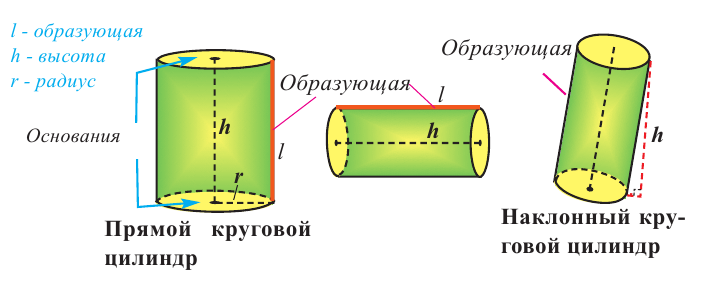
Цилиндром называется пространственная фигура, образованная двумя параллельными и конгруэнтными плоскими фигурами, которые совпадают при параллельном переносе, и отрезками, соединяющими соответствующие точки данных фигур. Плоские фигуры называются основаниями цилиндра, отрезки, соединяющие соответствующие точки основания называются образующими цилиндра. Если образующая перпендикулярна основанию, то цилиндр называется прямым, иначе – наклонным. Расстояние между основаниями называется высотой цилиндра.

На рисунках ниже изображены прямые и наклонные цилиндрические фигуры.

Сравнивая рисунки, изображенные ниже, можно сделать вывод, что призму можно рассматривать как частный случай цилиндра.

Прямой цилиндр, в основании которого лежит круг, называют прямым круговым цилиндром.

Далее, говоря о цилиндре, мы будем иметь в виду прямой круговой цилиндр. В любом другом случае будут отмечены его особенности.

Прямой круговой цилиндр также можно рассматривать как фигуру, полученную вращением прямоугольника вокруг одной из его сторон. Высота прямого кругового цилиндра равна его образующей. Радиусом цилиндра называется радиус круга в основании.

Вращая прямоугольник вокруг любой стороны, можно получить цилиндр, высота которого равна стороне прямоугольника.

Прямая, проходящая через центры оснований прямого кругового цилиндра называется осью цилиндра.

Площадь поверхности цилиндра

Площадь боковой и полной поверхностей цилиндра.

Изобразите на листе бумаги рисунки разверток цилиндров различных размеров, вырежьте и склейте цилиндры.

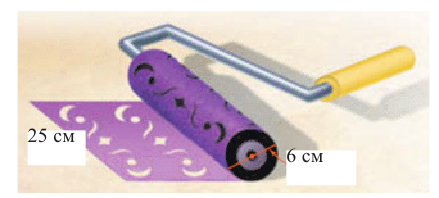
Мустафа красит стену цилиндрической кистью. Чтобы подсчитать время, потраченное на покраску, он захотел узнать, какую площадь покрывает кисть при одном полном обороте? Какие советы вы могли бы дать мальчику?

Так как кисть имеет цилиндрическую форму, то за один полный оборот кисть покрывает площадь в форме прямоугольника, равную боковой поверхности цилиндра.

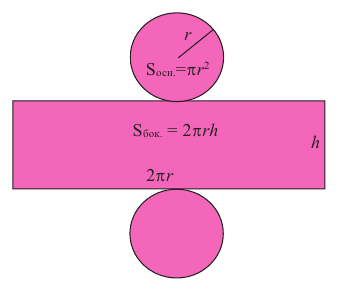
Полная поверхность цилиндра находится но формуле схожей с формулой полной поверхности призмы. Полная поверхность цилиндра состоит из боковой поверхности и двух конгруэнтных кругов.

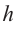
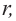
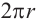
Боковую поверхность цилиндра с высотой и радиусом можно рассматривать как свернутый вокруг окружности прямоугольник со сторонами и

Боковая поверхность цилиндра равна произведению длины окружности основания и высоты.

Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований

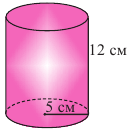
Пример №1

Найдите площадь полной поверхности цилиндра выстой 12 см и радиусом 5 см.

Решение:

Пример №2

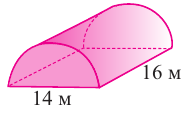
По данным рисунка, найдите площадь боковой поверхности прямого цилиндра, основанием которой являются полукруг.

Решение:

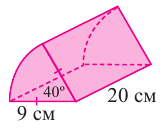
Пример №3

По данным на рисунке найдите площадь полной поверхности прямого цилиндра, основанием которой является круговой сектор с углом 40°.

Решение: известно, что

По формуле площади сектора:

Боковая поверхность фигуры равна 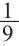части боковой поверхности цилиндра с радиусом 9 см и высотой 20 см плюс площадь двух конгруэнтных прямоугольников размерами

Таким образом,

Конус

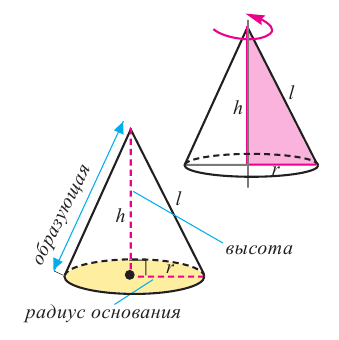
Конусом называется пространственная фигура, образованная всеми отрезками, соединяющими какую-либо плоскую фигуру с точкой, не принадлежащей данной плоскости. Плоскую фигуру называют основанием конуса, а точку –вершиной конуса.

Перпендикуляр, проведенный из вершины конуса на плоскость его основания, называется высотой конуса. Конус, в основании которого лежит круг, называется круговым конусом. Если ортогональная проекция вершины конуса лежит в центре основания, то конус называется прямым круговым конусом. Отрезок, соединяющий вершину конуса с любой точкой окружности основания кругового конуса, называется образующей конуса. В дальнейшем, говоря о конусе, будем иметь ввиду прямой круговой конус.

Конус можно рассматривать как фигуру, образованную вращением прямоугольного треугольника вокруг одного из катетов.

Прямая, выходящая из вершины конуса и проходящая через центр основания, называется осью конуса, радиус основания называется радиусом конуса. Для образующей, высоты и радиуса конуса справедливо отношение 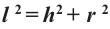(по теореме Пифагора)

Сооружение конуса

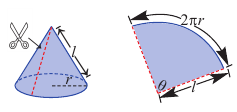
Известно, что при сворачивании прямоугольника можно получить цилиндр. Скручивая круговой сектор можно соорудить конус.

Радиус сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания.

Боковая поверхность конуса, полная поверхность конуса

Поверхность конуса состоит из боковой поверхности и круга в основании. На рисунке показаны радиус основания 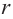и образующая

Боковая поверхность конуса – круговой сектор с радиусом 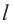и соответствующим центральным углом

Значит, площадь сектора и есть площадь боковой поверхности.

Значит, сектор составляет 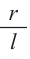часть окружности.

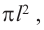
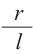
* Зная, что площадь круга тогда часть площади круга будет

Значит,

Боковая поверхность конуса равна произведению половины длины окружности основания и образующей.

* Площадь полной поверхности конуса

Пример №4

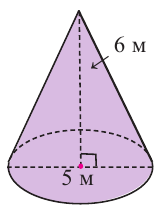
По рисунку найдите площадь боковой и полной поверхностей конуса.

Решение: Дано:

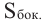
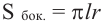
Найти: и

Чтобы найти образующую 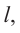применим теорему Пифагора

Сечения цилиндра и конуса плоскостью

Сечения поверхности конуса плоскостью (теория конических сечений) считались одной из вершин античной геометрии. Исследования Аполлония (3-й в.до н.э.) показали, что сечением плоскостью конуса, с бесконечной образующей (лучом) является: эллине (плоскость пересекает все образующие), парабола (плоскость сечения параллельна одной из образующих) или ветвь гиперболы (плоскость сечения параллельна двум образующим).

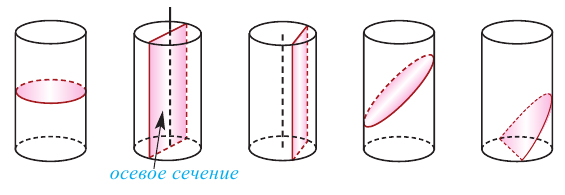
Сечения цилиндра плоскостью

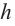
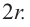
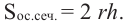
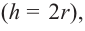
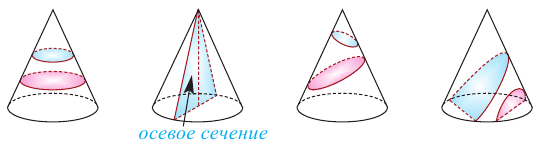
Сечением цилиндра плоскостью, параллельной основанию, является круг. Сечение цилиндра плоскостью, проходящей через ось симметрии, называется осевым сечением. Осевое сечение цилиндра является прямоугольником со сторонами и Значит, Цилиндр, осевое сечение которого является квадратом называется равносторонним цилиндром.

Сечения конуса плоскостью

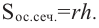
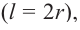
Сечением конуса плоскостью, параллельной основанию, является круг. Сечение конуса, проходящее через ось конуса называется осевым сечением конуса. Это сечение является равнобедренным треугольником, боковые стороны которого являются образующими, а основание равно диаметру конуса: Если осевое сечение конуса является правильным треугольником то конус называется равносторонним конусом.

Пример №5

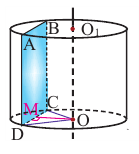
Сечением цилиндра плоскостью, проведенного параллельно оси цилиндра на расстоянии 3 см от оси, является квадрат, площадь которого равна 64 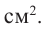Найдите площадь полной поверхности цилиндра.

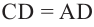
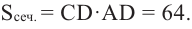
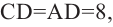
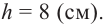
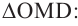
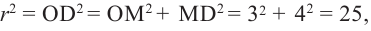
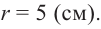
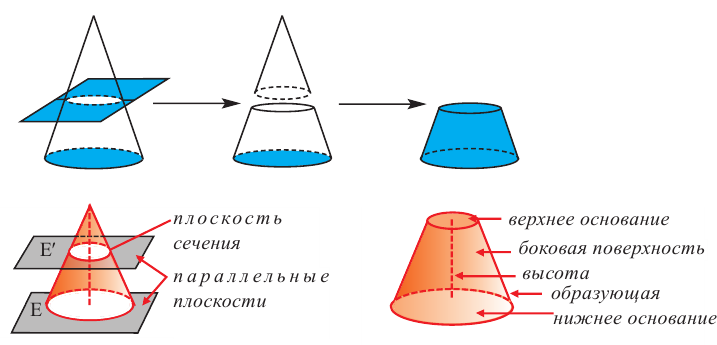
Решение: сначала найдем радиус и высоту цилиндра. По условию и Отсюда значит Из отсюда Таким образом,

Усеченный конус и площадь поверхности

Усеченный конус

Если параллельно основанию прямого кругового конуса провести плоскость, то получим маленький конус и усеченный конус.

Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.

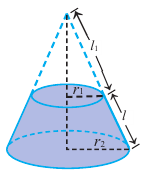
Боковая поверхность усеченного конуса равна разности боковых поверхностей большого конуса и маленького конуса, отсеченного плоскостью, параллельной основанию, от большого конуса. Используя обозначения на рисунке, можно записать:

Из подобия треугольников запишем следующее отношение

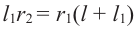
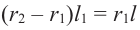
Тогда, подставив или в формулу для нахождения боковой поверхности, получим:

В данной формуле введем обозначение 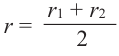среднего радиуса

усеченного конуса. Тогда

Полная поверхность усеченного конуса равна сумме боковой поверхности и площадей нижнего и верхнего оснований.

Пример №6

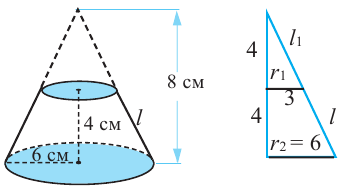
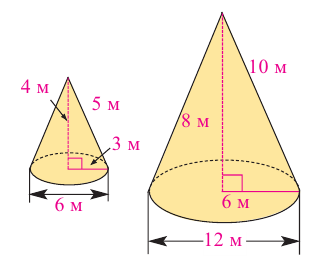
Конус высотой 8 см и радиусом 6 см рассечен плоскостью, параллельной основанию. Высота полученного усеченного конуса равна 4 см. Найдите площади боковой и полной поверхностей усеченного конуса

Решение: дано:

Найти:

Площадь поверхности шара и его частей

Шаром называется множество всех точек пространства находящихся от данной точки на расстоянии, не больше данного. Данная точка называется центром шара, данное расстояние радиусом 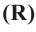шара.

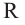
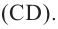
Множество всех точек, расположенных на расстоянии от центра шара, образует поверхность шара. Поверхность шара называется сферой. Прямая, соединяющая любые две точки на поверхности шара, называется хордой Хорда, проходящая через центр шара называется диаметром шара

Шар получается, при вращении полукруга вокруг диаметра.

Любое сечение шара плоскостью является кругом. Центр этого круга является основанием перпендикуляра, проведенного к плоскости и проходящего через центр шара. Если – радиус шара, – расстояние между плоскостью и центром, а – радиус сечения, то получим:

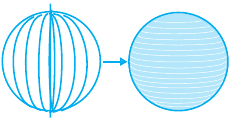
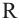
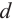
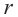
Пример №7

Шар радиуса 10 см пересечена плоскостью на расстояние

8 см от центра. Вычислите площадь сечения.

Решение: По условию

Тогда

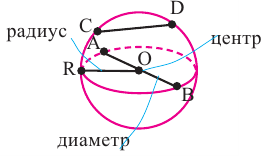
Сечение шара плоскостью, проходящей через центр шара, называется

большим кругом. Центр, радиус и диаметр большого круга равны

центру, радиусу и диаметру шара.

Также для шара известны следующие части:

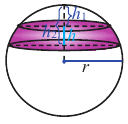
Площадь поверхности шара

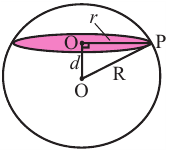
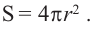
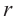
Площадь поверхности шара находится по формуле Здесь радиус шара.

В окружность радиусом 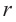впишем правильный многоугольник. Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур – конуса,усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника.

Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через

– площадь боковой поверхности конуса с образующей Так как то Умножим на 2 обе части равенства

Учитывая, что получим Значит,

– площадь боковой поверхности усеченного конуса.

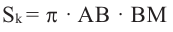
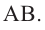
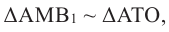
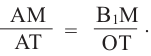
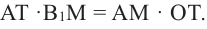
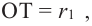
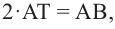
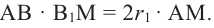
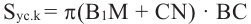
Зная, что 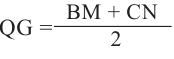получим, что

Так как 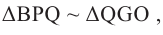то

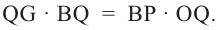
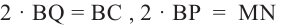
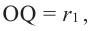
Умножим на 2 обе части равенства Учитывая,что

и получим

Значит,

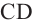
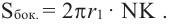
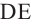
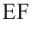
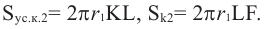
Понятно, что площадь боковой поверхности цилиндра с образующей равна Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей и конуса с образующей можно найти но формулам Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :

При бесконечном увеличении количества сторон многоугольника значение

стремится к радиусу, а площадь поверхности полученного тела к площади

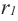
поверхности шара, т. е.

Площадь поверхности шара

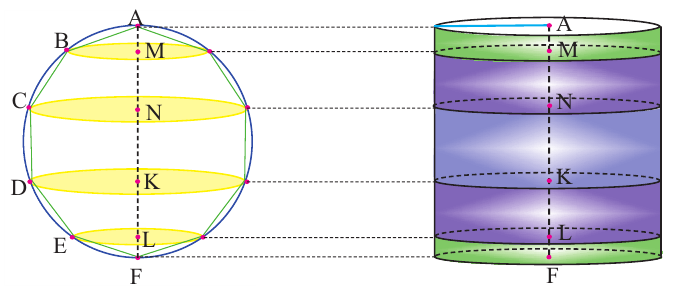
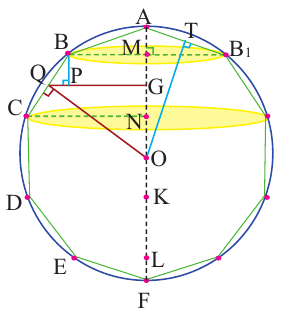
Доказательство Архимеда:

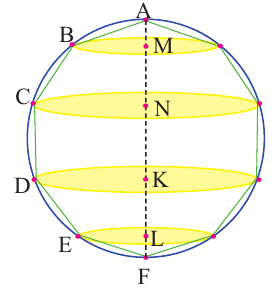
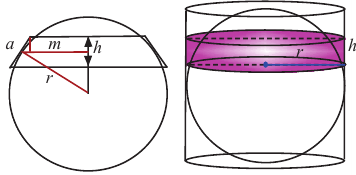
Пусть, в правильный многоугольник вписан круг, как показано на рисунке.

При вращении получается шар и покрывающее шар тело

Это тело состоит из двух усеченных конусов и цилиндра.

При увеличении количества сторон до бесконечности, тело будет стремится принять форму шара.

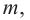
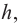
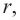
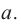
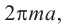
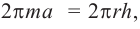
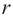
Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен а высота радиус шара сторона многоугольника, описанного вокруг большего круга равна Площадь боковой поверхности усеченного конуса будет а также т. е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен и высота

Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания 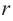и высотой

Т. е.,

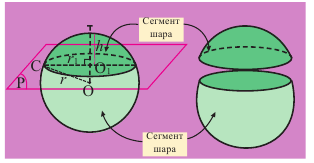
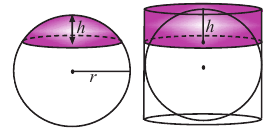
Площадь сегмента шара

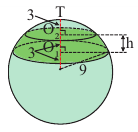
Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента.

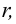
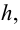
Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса площадь сферической поверхности сегмента высотой вычисляется по формуле

Площадь шарового пояса

Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом. Расстояние между параллельными плоскостями называется высотой шарового пояса.

Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.

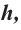
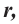
Площадь поверхности шарового пояса высотой отсекаемого от шара радиуса вычисляется по формуле

Пример №8

Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара 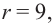найдите площадь поверхности шарового пояса.

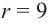
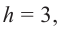
Решение: если и то площадь поверхности шарового пояса будет

Площади поверхностей подобных фигур

Отношение соответствующих линейных размеров подобных пространственных фигур постоянно и равно коэффициенту подобия.

Например, чтобы проверить подобны ли конусы на рисунке, найдем отношение соответствующих размеров. Если эти конусы подобны, то отношение радиусов должно быть равно отношению высот.

Значит эти конусы подобны и коэффициент подобия равен 2. Это говорит о том, что если все линейные размеры маленького конуса пропорционально увеличить в два раза, то получим конус, конгруэнтный большому конусу. Или наоборот, пропорционально уменьшив размеры большого конуса в два раза, получим конус, конгруэнтный маленькому. Если пропорционально увеличить или уменьшить размеры какой-либо фигуры, то можно получить подобные фигуры.

Отношение площадей подобных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия

Объем фигур вращения
Длина дуги кривой
Геометрические фигуры и их свойства
Основные фигуры геометрии и их расположение в пространстве
Вписанные и описанные многоугольники
Площадь прямоугольника
Объем пространственных фигур
Объёмы поверхностей геометрических тел

Источник

Площадь поверхности вращения тела

Пусть даны прямая и кривая Gamma , лежащая в одной плоскости с и расположенная по одну сторону от этой прямой. При вращении кривой Gamma вокруг оси получается поверхность lambda , площадь которой мы и хотим сначала определить, а потом вычислить (см. 46).

Начнем со случая, когда Gamma — отрезок, один конец которого отстоит от на , а другой — на (рис. 58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усеченного конуса) выражается формулой P(lambda)=pi(r+R)ell . В этом случае при r leqslant R имеем:

Прямая и кривая, лежащая в одной плоскости с прямой

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(1)

Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности.

То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения:

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(2)

где и — наименьшее и наибольшее расстояния точек ломаной от оси , и ell — длина ломаной.

Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть что Sigmaell_k=ell и для любого звена имеем r leqslant r_k и R_k leqslant R (здесь r_k и R_k — наименьшее и наибольшее расстояния точек k-ro звена от оси вращения).

Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги Gamma на части $gamma_0, gamma_1, ldots, gamma_{n-1}$ должно выполняться равенство

$P(lambda)= sum_{k=0}^{n-1} P(omega_k),$

(3)

где lambda — поверхность, полученная при вращении всей дуги Gamma , а omega_k — при вращении части gamma_k .

Если применить к каждой части omega_k неравенства (2), то получим, что

2picdot r_kcdot ell_k leqslant P(omega_k) leqslant 2picdot R_kcdot ell_k,,

где ell_k=ell(gamma_k) — длина дуги gamma_k , а r_k и R_k — наименьшее и наибольшее расстояния точек этой дуги gamma_k от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что

$2pi sum_{k=0}^{n-1} r_kell_k leqslant P(lambda) leqslant 2pi sum_{k=0}^{n-1} R_kell_k,.$

(4)

Иными словами, площадь поверхности вращения должна разделять множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr}.$

Именно это требование мы и примем за определение площади поверхности вращения.

Если Gamma — плоская спрямляемая кривая, лежащая по одну сторону от оси , то площадью поверхности lambda , получаемой при вращении этой кривой вокруг оси , называется число P(lambda) , разделяющее множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr},$

соответствующие всевозможным разбиениям дуги Gamma . Здесь r_k,,R_k и ell_k имеют указанный выше смысл.

Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой Gamma , выбрав в качестве параметра длину ell дуги , соединяющей в заданном направлении фиксированную точку кривой Gamma с произвольной точкой этой кривой (рис. 59). Тогда r_k и R_k будут наименьшими и наибольшими значениями ординаты для точек части gamma_k .

Произвольная точка на кривой

Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла $2piintlimits_{0}^{L} y(ell),dell$ , где через обозначена длина всей кривой Gamma . Поскольку функция y(ell) непрерывна в силу непрерывности кривой Gamma , то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т. е. число P(lambda) , разделяющее эти суммы, равняется интегралу:

$P(lambda)= 2piintlimits_{0}^{L} y(ell),dell,.$

(5)

Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая Gamma . Если она задана параметрически:

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} t_0 leqslant t leqslant T$ , то $dell= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$ ,

и формула (5) принимает вид:

$P(lambda)= 2pi intlimits_{t_0}^{T} psi(t) sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$

(6)

(когда ell меняется от до , переменная { t} меняется от ${ t_0}$ до ).

В частности, если кривая Gamma задана явным уравнением y=f(x),~ a leqslant x leqslant b , то

$P(lambda)= 2pi intlimits_{a}^{b} f(x) sqrt{1+bigl(f'(x)bigr)^2},dx= 2pi intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.$

(7)

Если кривая Gamma задана в полярных координатах уравнением rho=f(varphi) , где alpha leqslant varphi leqslant beta , а функция имеет непрерывную производную f'(varphi) на [alpha;beta] , то, учитывая, что y= rhosinvarphi= f(varphi)sinvarphi , a $dell= sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi$ , получим:

$P=2pi intlimits_{alpha}^{beta} rhosinvarphi sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi,.$

(8)

Пример 1. Найдем площадь поверхности шара радиуса .

Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности x^2+y^2=R^2 вокруг оси . Тогда площадь поверхности шара найдется по формуле

$P=2pi intlimits_{-R}^{R} ysqrt{1+(y')^2},dx,.$

Так как $y=sqrt{R^2-x^2}$ — функция четная, то

$P=4pi intlimits_{0}^{R} ysqrt{1+(y')^2},dx,.$

Найдя $y'= frac{-x}{sqrt{R^2-x^2}}$ и вычислив сумму $1+(y')^2= 1+frac{x^2}{R^2-x^2}= frac{R^2}{R^2-x^2}$ , получим:

$P= 4pi intlimits_{0}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 4pi Rintlimits_{0}^{R}dx= Bigl.{4pi Rx}Bigr|_{0}^{R}= 4pi nR^2.$

Пример 2. Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг Ox:

$begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0 leqslant t leqslant 2pi,.$

Решение. Найдем $x'_t=a(1-cos{t}),~ y'_t=asin{t}$ . Тогда

$(x'_t)^2+(y'_t)^2= 2a^2(1-cos{t})= 4a^2sin^2frac{t}{2},.$

Искомая площадь поверхности вращения равна

$begin{aligned}P&= 2pi intlimits_{0}^{2pi} a(1-cos{t})2asin frac{t}{2},dt= 8pi a^2 intlimits_{0}^{2pi}sin^3 frac{t}{3},dt= 8pi a^2 intlimits_{0}^{2pi}! left(1-cos^2 frac{t}{2} right)! sin frac{t}{2},dt=\ &= left.{8pi a^2! left(-2cos frac{t}{2}+ frac{2}{3}cos^3 frac{t}{2}right)}right|_{0}^{2pi}= frac{64}{3},pi a^2.end{aligned}$

Пример 3. Найдем площадь поверхности, образованной вращением лемнискаты rho^2=a^2cos2varphi вокруг полярной оси.

Решение. Имеем: $rho= asqrt{cos2varphi}~ Rightarrow~ rho'_{varphi}= frac{-asin2varphi}{sqrt{cos2varphi}}$ . Поэтому

$rho^{2}+rho_{varphi}^{prime2}= a^2cos2varphi+ frac{a^{2} sin^{2}2varphi}{cos2varphi}= a^2! left(cos2varphi+ frac{sin^{2}2varphi}{cos2varphi}right)= frac{a^{2}}{cos2varphi},.$

Пользуясь формулой (8) для вычисления площади поверхности в полярных координатах, найдем сначала половину искомой площади поверхности:

$frac{1}{2}P= 2pi intlimits_{0}^{pi/4} asqrt{cos2varphi}, frac{sinvarphicdot a}{sqrt{cos2varphi}}, dvarphi= 2pi a^2 intlimits_{0}^{pi/4} sinvarphi,dvarphi= 2pi a^2cdot frac{2-sqrt{2}}{2}= pi a^2bigl(2-sqrt{2}bigr).$

Вся площадь данной поверхности будет равна $P=2bigl(2-sqrt{2}bigr)pi a^2$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

I Определения

Определение
1. Поверхность
вращения – это поверхность, которая
получается при вращении плоской линии

вокруг оси, лежащей в её плоскости и не
пересекающей её.

Ось вращения может
и пересекать линию, если это ось симметрии
линии. В этом случае рассматривают лишь
«половину» линии.

Впишем в кривую
произвольную ломанную и обозначимдлину наибольшего её звена. При вращении
этой ломанной вокруг оси мы получим
поверхность,
составленную из боковых поверхностей
усеченных конусов. Обозначим площадь
этой поверхности.

Определение
2. Конечный
предел
называют площадью поверхности вращения.

Можно показать,
что если линия
имеет длину, то поверхность, полученная
её вращением, имеет площадь.

II Общая формула

Линия
,
вращением которой вокруг оси абсцисс
получена поверхность, может быть задана
одним из следующих способов:

1) 2) 3)

Теорема.
Если функции, определяющие линию,
непрерывны вместе со своими производными,
то площадь поверхности вращения (вокруг
оси
)
определяется формулой:

(1)

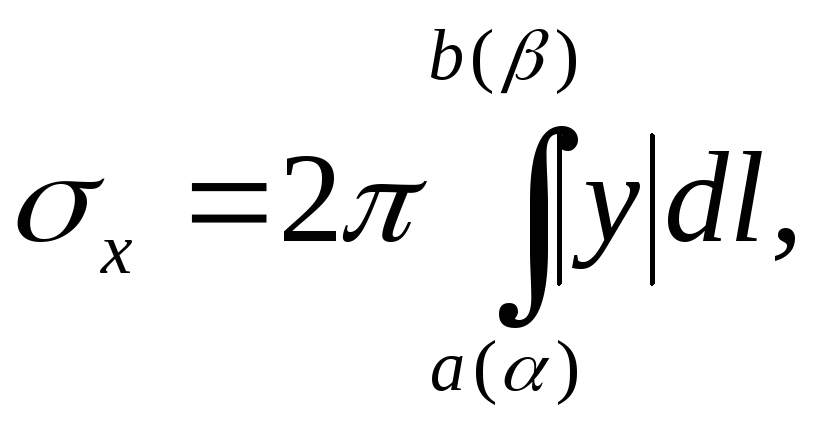
где
– подынтегральное выражение, фигурирующее
в соответствующей формуле для длины
дуги.

Идея
доказательства.
Пусть концы -го
звена ломанной имеют координаты
и .
Это звено при вращении вокруг оси
опишет
боковую поверхность усеченного конуса
с радиусами основанийии образующей(длина-го
звена). Для площади такой поверхности
известна формула

Вся ломанная даст
поверхность с площадью

Если, например,
имеющаяся кривая – это график функции
,
тогда
(см. §3, II). Также,
заменяя
на
получим

В этой сумме
нетрудно увидеть интегральную сумму,
которая в пределе даст интеграл из (1).

III Частные случаи и примеры

1) Найти площадь
сферического пояса, полученного вращением
дуги окружности ,
,
вокруг оси абсцисс.

Формула имеет вид

Проведём
предварительные вычисления:

,
.

Теперь вычисляем
площадь:

Сферический пояс
– это часть сферы, заключенная между
двумя параллельными плоскостями.
Полученный результат показывает, что
площадь сферического пояса зависит
лишь от расстояния между плоскостями,
и не зависит от их положения относительно
сферы.

2) Найти площадь
поверхности, полученной вращением
астроиды ,
вокруг оси
.

Общая формула
принимает вид

Астроида симметрична
относительно оси вращения. Поэтому
необходимо рассматривать лишь часть
её, например, для
.
Предварительные вычисления:

, ,

Так как
то, чтобы не «разбираться» с модулем,
воспользуемся симметрией астроиды
относительно оси
,
т.е. будем рассматривать:

3) Дуга кардиоиды
,,
вращается вокруг полярной оси. Найти
объём тела вращения.

Формула (1) в этом
случае принимает вид:

Имеем для кардиоиды

Задачи
для самостоятельного решения.

1. Найти площадь
поверхности тора, полученного вращением
окруж-ности ,
,
вокруг оси
.

2. Круговой сегмент,
основание которого
,
высота,
вращается вокруг основания. Найти
площадь поверхности получающегося тела
вращения.

3. Первая арка
циклоиды
,,,
вращается: а) вокруг оси;
б) вокруг оси.
Найти площади получающихся поверхностей
вращения.

Соседние файлы в папке Лекции по мат.анализу

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 ноября 2021 года; проверки требует 1 правка.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — гиперболоид. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Поверхность, полученная вращением кривой x=2+cos z вокруг оси z

Является объектом изучения в математическом анализе, аналитической, дифференциальной и начертательной геометрии.

Примеры[править | править код]

Круговая цилиндрическая поверхность (получается вращением прямой вокруг параллельной ей прямой).
Конус (получается вращением прямой вокруг другой прямой, пересекающей первую).
Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).
Тор (получается вращением окружности вокруг не пересекающей её оси, лежащей в той же плоскости).
Эллипсоид вращения ― эллипсоид, длины двух полуосей которого совпадают (получается вращением эллипса вокруг одной из его осей).
Параболоид вращения ― эллиптический параболоид, полученный вращением параболы вокруг своей оси.
Катеноид (получается вращением цепной линии).

Площадь[править | править код]

Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой. Это утверждение называется второй теоремой Паппа — Гульдина, или теоремой Паппа о центроиде.

Например, для тора с радиусами , площадь поверхности равна

$S=(2pi r)cdot (2pi R)=4pi ^{2}rR$

Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

$S=2pi int limits _{a}^{b}f(x){sqrt {1+left(f'(x)right)^{2}}}dx$

Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

$S=2pi int limits _{alpha }^{beta }y(t){sqrt {left(x'(t)right)^{2}+left(y'(t)right)^{2}}}dt$

Для случая, когда кривая задана в полярной системе координат действительна формула

$S=2pi int limits _{alpha }^{beta }rho (varphi )|sin varphi |{sqrt {left(rho (varphi )right)^{2}+left(rho '(varphi )right)^{2}}}dvarphi$

Объём[править | править код]

Объём, ограниченный поверхностью вращения, образованной вращением плоской замкнутой несамопересекающейся кривой вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равен произведению площади плоской фигуры, ограниченной кривой, на длину окружности с радиусом, равным расстоянию от оси до центра тяжести плоской фигуры.

Объём поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

$V=pi int limits _{a}^{b}f^{2}(x)dx$

Вариации и обобщения[править | править код]

Искривлённое произведение

Примечания[править | править код]

Источник

Смотрите также

Определение фигур вращения

Цилиндр

Площадь поверхности цилиндра

Пример №1

Пример №2

Пример №3

Конус

Сооружение конуса

Боковая поверхность конуса, полная поверхность конуса

Пример №4

Сечения цилиндра и конуса плоскостью

Сечения цилиндра плоскостью

Сечения конуса плоскостью

Пример №5

Усеченный конус и площадь поверхности

Пример №6

Площадь поверхности шара и его частей

Пример №7

Площадь поверхности шара

Площадь поверхности шара

Площадь сегмента шара

Площадь шарового пояса

Пример №8

Площади поверхностей подобных фигур

Площадь поверхности вращения тела

I Определения

II Общая формула

1) 2) 3)

III Частные случаи и примеры

Примеры[править | править код]

Площадь[править | править код]

Объём[править | править код]

Вариации и обобщения[править | править код]

Примечания[править | править код]

Вам также может понравиться

Как найти пряжу по составу

Как найти моду все формулы

Математика как найти семью

Добавить комментарий Отменить ответ