Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн – от профильных экспертов Студворк!
Тест по теме «Площадь параллелограмма»

{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
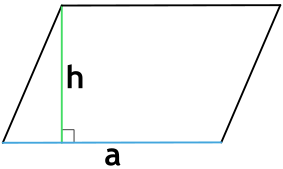
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
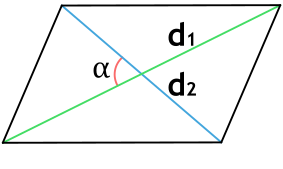
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
Загрузить PDF
Загрузить PDF
Параллелограмм определяется как простой четырехугольник с двумя парами параллельных сторон. Если вы занимаетесь геометрией, то вам может понадобиться найти площадь параллелограмма. Вот несколько указаний как именно это сделать.
Шаги
-

1
Найдите основание параллелограмма. Основание – это длина нижней стороны параллелограмма.
-

2
Найдите высоту параллелограмма. Высота параллелограмма – это перпендикулярная линия, проведенная из произвольной точки верхней стороны к нижней стороне параллелограмма.
-

3
Умножьте основание на высоту.
Реклама
Об этой статье
Эту страницу просматривали 9132 раза.
Была ли эта статья полезной?
Площадь параллелограмма
Алик Беникович Айрапетян
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На данной странице вы можете ознакомиться с разнообразными вариантами формул для вычисления площади параллелограмма.
Здесь же размещены простые в использовании калькуляторы, с помощью которых можно быстро узнать, как найти площадь параллелограмма по двум сторонам, диагоналям и углу между ними, или через другие величины.
Приведены примеры решения подобных задач.
Рассмотрим задачу и разберёмся на примере, как найти площадь параллелограмма по стороне и высоте, опущенной на эту сторону.
Сделаем это для того, чтобы вы могли проследить за ходом решения и выявить ошибки в своих работах, а также для возможности сравнения своего ответа с ответом калькулятора.
Пример 1
Дано:
сторона параллелограмма = $5$ см, высота = $7$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 5 cdot 7 = 35$ см$^2$.
Ответ:
$S = 35$ см$^2$.
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

Формула площади параллелограмма по стороне и высоте, опущенной на эту сторону:
$S = b cdot h1$, где
$S$ — площадь параллелограмма,
$b$ — сторона,
$h1$ — высота, опущенная на неё.
Площадь параллелограмма по двум сторонам и углу между ними

Формула площади параллелограмма по двум сторонам и углу между ними:
$S = a cdot b cdot sin (α)$, где
$S$ — площадь параллелограмма,
$a$ — сторона номер один,
$b$ — сторона номер два,
$α$ — угол между сторонами $a$ и $b$.
Чтобы проверить свое понимание темы, рассмотрим также пример задачи на нахождение площади параллелограмма по основанию и высоте и также сверим свой ответ с результатом калькулятора.
Пример 2
Дано:
основание $a = 10$ см, высота $h = 7$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 10 cdot 7 = 70$ см$^2$.
Ответ:
$S = 70$ см$^2$.
Площадь параллелограмма по основанию и высоте

Формула площади параллелограмма по основанию и высоте:
$S = a cdot h$, где
$S$ — площадь параллелограмма,
$a$ — основание,
$h$ — высота.
Площадь параллелограмма по двум диагоналям и углу между ними

Формула площади параллелограмма по двум диагоналям и углу между этими диагоналями:
$S = d1 cdot d2 cdot sin (α)$, где
$S$ — площадь параллелограмма,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями $d1$ и $d2$.
В качестве ещё одного примера рассмотрим задачу на нахождение площади параллелограмма по вписанной окружности и стороне.
Пример 3
Дано:
сторона параллелограмма $a = 6$ см, радиус вписанной окружности = $5$ см.
Найти:
площадь параллелограмма $S$.
Решение:
$S = 2 cdot 6 cdot 5 = 60 $ см$^2$.
Ответ:
$S = 60 $ см$^2$.
Площадь параллелограмма по вписанной окружности и стороне

Формула площади параллелограмма по вписанной окружности и стороне:
$S = 2 cdot a cdot r$, где
$S$ — площадь параллелограмма,
$a$ — сторона,
$r$ — радиус вписанной окружности.
Площадь параллелограмма по вписанной окружности и углу между сторонами

Формула площади параллелограмма по вписанной окружности и углу между сторонами:
$S = frac{4 cdot R^2} {sin (α)}$, где
$S$ — площадь параллелограмма,
$R$ — радиус вписанной окружности,
$α$ — угол между сторонами.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 10.06.2019
1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма
α, β – углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

Калькулятор – вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ
d –меньшая диагональ
α, β – углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):

Калькулятор – вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
