Как найти площадь правильного равностороннего треугольника

Как найти площадь правильного равностороннего треугольника

Как найти площадь равностороннего треугольника

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как найти площадь равностороннего треугольника

Чтобы найти площадь равностороннего (правильного, равноугольного) треугольника воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Равносторонний (правильный) треугольник

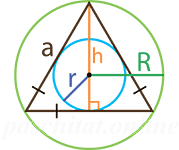
Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):

  • длину равных сторон (a)
  • высоту (h)
  • радиус описанной окружности (R)
  • радиус вписанной окружности (r)
  • периметр треугольника (P)

Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).

Как посчитать площадь равностороннего треугольника зная длину равных сторон

Чему равна площадь равностороннего треугольника если длина стороны

a =

?

Ответ:

S =

0

Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?

Формула

S =√3/4 ⋅ a²

Пример

Если сторона a = 2 см, то:

S = √3/4 ⋅ 2² = 1.732/4 ⋅ 4 ≈ 1.732 см2

Как посчитать площадь равностороннего треугольника зная его высоту

Чему равна площадь равностороннего треугольника если его

высота h =

?

Ответ:

S =

0

Какова площадь равностороннего треугольника (S) если известна его высота (h)?

Формула

S =h² / √3

Пример

Если высота h = 3 см, то:

S = 3²/√3= 9/1.732 ≈ 5.19 см2

Как посчитать площадь равностороннего треугольника зная радиус описанной окружности

Чему равна площадь равностороннего треугольника если радиус описанной окружности

R =

?

Ответ:

S =

0

Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?

Формула

S =3⋅√3/4 ⋅ R²

Пример

Если радиус описанной окружности R = 4 см, то:

S = 3 ⋅ √3/4 ⋅ 4² = 3 ⋅ 1.732/4 ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см2

Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности

Чему равна площадь равностороннего треугольника если радиус вписанной окружности

r =

?

Ответ:

S =

0

Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?

Формула

S =3⋅√3 ⋅ r²

Пример

Если радиус вписанной окружности r = 1 см, то:

S = 3⋅√3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см2

Как посчитать площадь равностороннего треугольника зная его периметр

Чему равна площадь равностороннего треугольника если его периметр

P =

?

Ответ:

S =

0

Какова площадь равностороннего треугольника (S) если известен его периметр (P)?

Формула

S =√3/36 ⋅ P²

Пример

Если периметр P = 8 см, то:

S = √3/36 ⋅ 8² = 1.732/36 ⋅ 64 ≈ 3 см2

См. также

Источник

Как посчитать площадь треугольника:

Через сторону

Через сторону и высоту

Через высоту

Укажите размеры:

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Треугольник – это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Равносторонний треугольник – это треугольник у которого длины всех сторон равны.

Треугольники по своей форме бывают прямоугольный, равнобедренный, равносторонний, разносторонний.

Формула площади равностороннего треугольника

Посчитать площадь равностороннего треугольника можно посчитать тремя способами.

Площадь равностороннего треугольника расчитывается по одной из формул:

a
a
a
h

Через сторону и высоту:

S = dfrac{1}{2}ah

Через сторону:

S = dfrac{sqrt{3}}{4} a^2

Через высоту:

S = dfrac{h^2}{sqrt{3}}

  • S – площадь треугольника
  • a – равные стороны
  • b – основание треугольника
  • h – высота

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Содержание

  • 1 Свойства
  • 2 Правильный сферический треугольник
  • 3 Теоремы о равностороннем треугольнике или содержащие его
  • 4 См. также
  • 5 Примечания

Свойства[править | править код]

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

  • Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
r = frac{sqrt 3}{6} a
  • Радиус описанной окружности правильного треугольника, выраженный через его сторону:
R = frac{sqrt 3}{3} a
  • Периметр правильного треугольника:
P = 3a = 3 sqrt 3 R = 6 sqrt 3 r
  • Высоты, медианы и биссектрисы правильного треугольника:
h = m = l = frac{sqrt 3}{2} a
  • Площадь правильного треугольника рассчитывается по формулам:
S={frac {{sqrt 3}}{4}}a^{2}={frac {3{sqrt 3}}{4}}R^{2}=3{sqrt 3}r^{2}={frac {{sqrt 3}}{36}}P^{2}
  • Радиус описанной окружности равен двойному радиусу вписанной окружности:
R = 2r
  • Правильными треугольниками можно замостить плоскость.
  • В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.

Правильный сферический треугольник[править | править код]

Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.

Теоремы о равностороннем треугольнике или содержащие его[править | править код]

  • Задача Наполеона
  • Прямая Симсона одно из свойств
  • Теорема Вивиани
  • Теорема Морли
  • Теорема Наполеона
  • Теорема Помпею
  • Теоремы Тебо 2 и 3
  • Точки Аполлония
  • Точки Торричелли

См. также[править | править код]

  • Замечательные прямые треугольника
  • Замечательные точки треугольника
  • Равнобедренный треугольник
  • Теорема Чевы
  • Треугольник
  • Треугольник Рёло

Примечания[править | править код]

Перейти к шаблону «Символ Шлефли» 

Символ Шлефли
Многоугольники
  • {1}
  • {2}
  • {3}
  • {4}
  • {5}
  • {6}
  • {7}
  • {8}
  • {9}
  • {10}
  • {11}
  • {12}
  • {14}
  • {15}
  • {17}
  • {18}
  • {20}
  • {30}
  • {51}[de]
  • {257}
  • {65537}
  • {4294967295}
  • {∞}
Звёздчатые многоугольники
  • {5/2}
  • {6/2}
  • {7/2}
  • {7/3}
  • {8/2}
  • {8/3}
  • {9/2}
  • {9/3}
  • {9/4}
Паркеты на плоскости
  • {3,6}
  • {4,4}
  • {6,3}
Правильные многогранники
и сферические паркеты
  • {2,n}
  • {3,3}
  • {4,3}
  • {3,4}
  • {5,3}
  • {3,5}
  • {n,2}
Многогранники Кеплера — Пуансо
  • {5/2,5}
  • {5,5/2}
  • {5/2,3}
  • {3,5/2}
Соты

{4,3,4}
Четырёхмерные многогранники
  • {3,3,3}
  • {4,3,3}
  • {3,3,4}
  • {3,4,3}
  • {5,3,3}
  • {3,3,5}
Источник

Как найти площадь равностороннего треугольника?

Площадь равностороннего треугольника можно найти и через сторону и проведенную к ней высоту, и через три стороны (по формуле Герона).

Но удобнее всего использовать формулу для вычисления площади треугольника по двум сторонам:

    [S = frac{1}{2}absin alpha ]

ploschad ravnostoronnego treugolnika

Все стороны равностороннего треугольника равны между собой: b=a.

Все углы равностороннего треугольника равны по 60 градусов.

Подставляем b=a и α=60º:

    [S = frac{1}{2}absin alpha = frac{1}{2}a cdot a cdot sin {60^o}]

Подставляем значение синуса 60 градусов:

    [S = frac{1}{2}{a^2} cdot frac{{sqrt 3 }}{2} = frac{{{a^2}sqrt 3 }}{4}.]

Таким образом,

formula ploschadi ravnostoronnego treugolnikaформула для нахождения площади равностороннего треугольника:

    [S = frac{{{a^2}sqrt 3 }}{4}.]

Источник

Добавить комментарий