Как найти площадь призмы через цилиндр - Сайт, где вы сможете решить свои вопросы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.

Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
Примеры задач

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

S_полн. = S_бок. + 2S_осн.

Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.

S_бок. = P_осн. ⋅ h

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.


Площадь	Формула
основание
боковая поверхность	S_бок. = 3ah
полная

microexcel.ru

3. Площадь правильной четырехугольной призмы

Основание: квадрат.


Площадь	Формула
основание	S_осн. = a²
боковая поверхность	S_бок. = 4ah
полная	S_полн. = 2a² + 4ah

microexcel.ru

Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a². А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a².

4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник


Площадь	Формула
основание
боковая поверхность	S_бок. = 6ah
полная

microexcel.ru

Примеры задач

Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.

Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:

Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см². Найдите ее высоту, если известно, что сторона основания равна 5 см.

Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

Источник

Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.

Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.

Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.

Окружность основания цилиндра описана около многоугольника основания призмы.

Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.

Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.

Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны

180°

Формулы вычисления радиуса (R) описанной окружности

(a, b, c) — стороны, (h) — высота, (d) — диагональ.

Правильный треугольник	(R =) 23h; (R=) a33
Прямоугольный треугольник	(R=) 12 гипотенузы
Произвольный треугольник	R=abc4S;R=a2sinα
Квадрат	(R =) a22
Прямоугольник	(R =) d2
Правильный шестиугольник	(R = a)

Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.

Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.

Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.

Окружность основания цилиндра вписана в многоугольник основания призмы.

Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.

Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.

Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.

Формулы вычисления радиуса (r) вписанной окружности

Где (h) — высота, (S) — площадь, (p) — полупериметр, (a) — сторона.

Правильный треугольник	r=13h;r=a36
Произвольный (и прямоугольный) треугольник	(r =) Sp
Квадрат
Ромб	или
Правильный шестиугольник	(r =) a32

Источник

Перейти к содержанию

Цилиндр вписан в правильную четырехугольную призму

На чтение 1 мин. Просмотров 6.3k.

Цилиндр вписан в правильную четырехугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

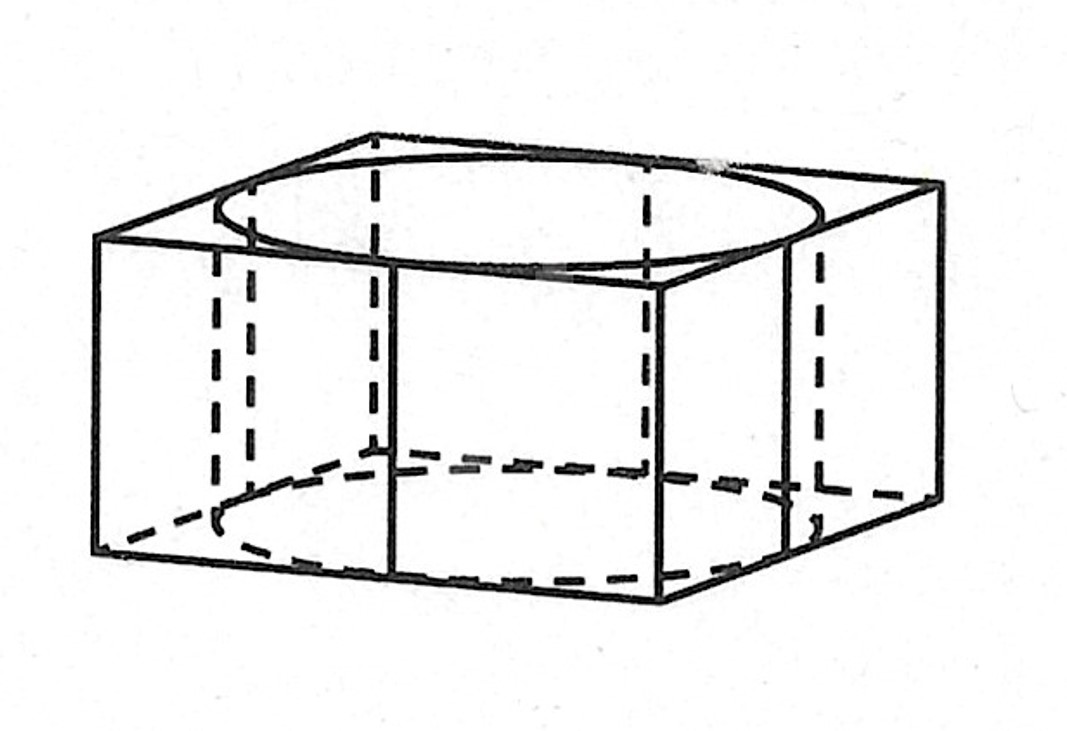
Решение: Площадь боковой поверхности призмы — это сумма площадей боковых прямоугольников. Для того, чтобы найти площадь прямоугольника нам надо знать его стороны. Высоту призмы мы уже знаем — это 3. Высота призмы равна высоте цилиндра, так как цилиндр вписан в призму, а значит, его основания содержатся в основаниях призмы.

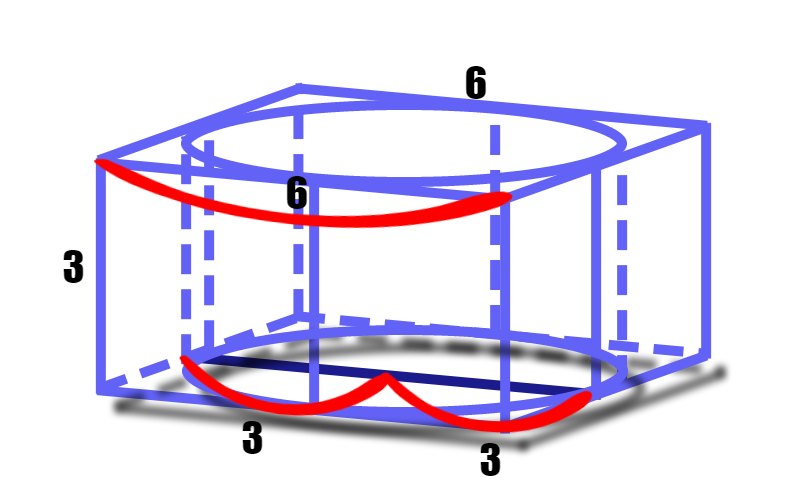
Отметим на рисунке диаметр основания цилиндра (темно-синяя линия). Очевидно, что диаметр основания цилиндра равен стороне боковой грани призмы. Таким образом, получаем, что ширина боковой грани призмы 6. Значит, площадь одной грани будет .

Таких граней четыре. Значит надо 18 умножить на 4 и мы найдем площадь боковой поверхности призмы.

Ответ: 72

( 3 оценки, среднее 5 из 5 )

Источник

Призма описана около цилиндра, если ее основания — многоугольники, описанные около оснований цилиндра. Соответственно, цилиндр вписан в призму.

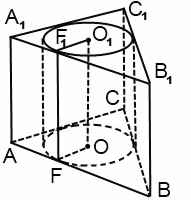
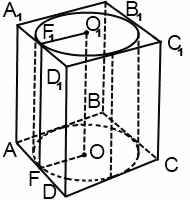
Цилиндр можно вписать в призму, если в основание призмы можно вписать окружность. Радиус вписанной окружности равен радиусу цилиндра. Высоты цилиндра и призмы равны. В школьном курсе изучается только прямой круговой цилиндр, соответственно, цилиндр в этом случае вписан в прямую призму.

Боковые грани описанной около цилиндра призмы являются касательными плоскостями к боковой поверхности цилиндра.

Найдем отношение объема призмы к объему вписанного в нее цилиндра:

$[frac{{{V_1}}}{{{V_2}}} = frac{{{S_{ocn}} cdot H}}{{pi {r^2}H}} = frac{{prH}}{{pi {r^2}H}} = frac{p}{{pi r}}.]$

p — полупериметр основания призмы, r — радиус вписанной в основание призмы окружности и радиус цилиндра, H — высота призмы и высота цилиндра.

В частности, отношение объема правильной треугольной призмы к объему вписанного цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{frac{{3a}}{2}}}{{pi cdot frac{a}{{2sqrt 3 }}}} = frac{{3sqrt 3 }}{pi }.]$

Отношение объема правильной четырехугольной призмы к объему вписанного цилиндра

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{2a}}{{pi cdot frac{a}{2}}} = frac{4}{pi }.]$

Для правильной шестиугольной призмы это отношение равно

$[frac{{{V_1}}}{{{V_2}}} = frac{p}{{pi r}} = frac{{3a}}{{pi cdot frac{{asqrt 3 }}{2}}} = frac{6}{{pi sqrt 3 }} = frac{{2sqrt 3 }}{pi }.]$

Отношение площади боковой поверхности призмы к боковой поверхности вписанного цилиндра:

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}} cdot H}}{{2pi rH}} = frac{{{P_{ocn}}}}{{2pi r}}.]$

Поскольку половина периметра основания — полупериметр,

$[frac{{{P_{ocn}}}}{2} = p, Rightarrow frac{{{S_1}}}{{{S_2}}} = frac{p}{{pi r}}.]$

Таким образом, если цилиндр вписан в призму, отношение площади боковой поверхности призмы к боковой поверхности цилиндра равно отношению объема призмы к объему вписанного цилиндра. В частности, отношение площади боковой поверхности правильной треугольной призмы к площади боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{3a}}{{2pi cdot frac{a}{{2sqrt 3 }}}} = frac{{3sqrt 3 }}{pi }.]$

Отношение боковой поверхности правильной четырехугольной призмы к боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{4a}}{{2pi cdot frac{a}{2}}} = frac{4}{pi }.]$

Отношение боковой поверхности правильной шестиугольной призмы к боковой поверхности вписанного цилиндра

$[frac{{{S_1}}}{{{S_2}}} = frac{{{P_{ocn}}}}{{2pi r}} = frac{{6a}}{{2pi cdot frac{{asqrt 3 }}{2}}} = frac{6}{{pi sqrt 3 }} = frac{{2sqrt 3 }}{pi }.]$

При решении задач, в которых цилиндр вписан в призму, можно рассматривать часть сечения комбинации тел плоскостью, проходящей через ось цилиндра. Для прямой призмы это сечение — прямоугольник, стороны которого равны радиусу цилиндра и высоте цилиндра. Например, AA1O1O: AA1=H, AO=r.

Источник

Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.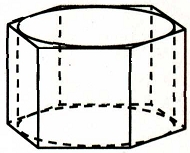

Источник: mathege, Ященко ЕГЭ 2022 (36 вар).

Решение:

Правильная шестиугольная призма – это шестиугольная призма у которой 2 основания правильные шестиугольники, а боковые грани 6 равны прямоугольников.
Площадь боковой поверхности данной призмы – это площадь 6-х равных прямоугольников.
Высота прямоугольника равна высоте цилиндра h = 2. Длина прямоугольника а, является стороной правильного шестиугольника и находится через радиус вписанной окружности по формуле:

a=frac{2cdot r}{sqrt{3}}=frac{2cdot sqrt{3}}{sqrt{3}}=2

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 6·S_{прямоугольника} = 6·h·a = 6·2·2 = 24

Ответ: 24.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.6 / 5. Количество оценок: 220

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Формула площади правильной призмы

1. Общая формула

2. Площадь правильной треугольной призмы

3. Площадь правильной четырехугольной призмы

4. Площадь правильной шестиугольной призмы

Примеры задач

Цилиндр вписан в правильную четырехугольную призму

Вам также может понравиться

Как найти телефон по часам самсунг

Террария как найти наживку для рыбалки

Как быстро найти все анемокулы

Добавить комментарий Отменить ответ