Версия для печати и копирования в MS Word
1
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен
а высота равна 2.
2
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
3
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 1.
4
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 2.
5
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 1.
6
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
7
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
8
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
9
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
10
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
11
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 2.
12
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
13
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
14
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
15
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 4.
16
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 1.
17
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 2.
18
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 1.
19
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
20
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 2.
21
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
22
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
23
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
24
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
25
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна 3.
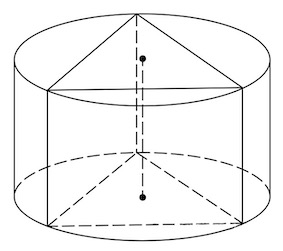
Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.


Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.
Например, цилиндр всегда можно описать около прямой треугольной призмы, около правильной призмы.
Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т. к. высота призмы равна высоте цилиндра.
Окружность основания цилиндра описана около многоугольника основания призмы.
Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.
Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны
180°
.
Формулы вычисления радиуса (R) описанной окружности
(a, b, c) — стороны, (h) — высота, (d) — диагональ.
| Правильный треугольник | (R =) 23h; (R=) a33 |
| Прямоугольный треугольник | (R=) 12 гипотенузы |
| Произвольный треугольник | R=abc4S;R=a2sinα |
| Квадрат |
(R =) a22 |
|
Прямоугольник |
(R =) d2 |
|
Правильный шестиугольник |
(R = a) |
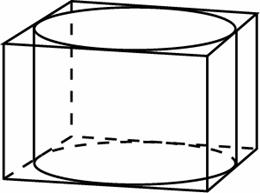
Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.
Например, цилиндр всегда можно вписать в прямую треугольную призму, в правильную призму.
Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинаций этих тел, т. к. высота цилиндра равна высоте призмы.
Окружность основания цилиндра вписана в многоугольник основания призмы.
Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.
Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.
Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.
Формулы вычисления радиуса (r) вписанной окружности
Где (h) — высота, (S) — площадь, (p) — полупериметр, (a) — сторона.
| Правильный треугольник | r=13h;r=a36 |
| Произвольный (и прямоугольный) треугольник | (r =) Sp |
| Квадрат | |
| Ромб |
или |
| Правильный шестиугольник | (r =) a32 |
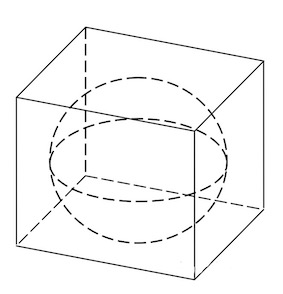
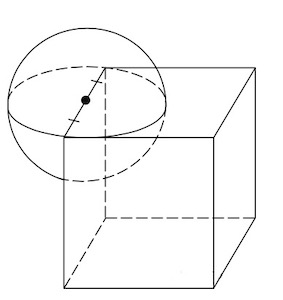
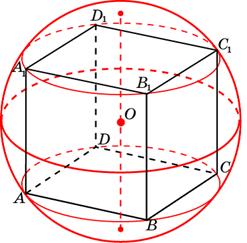
Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.
Решение: + показать
Задача 2. В куб вписан шар радиуса Найдите объем куба.
Решение: + показать
Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.
Решение: + показать
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен
Найдите высоту цилиндра.
Решение: + показать
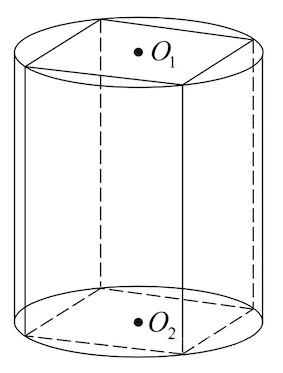
Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.
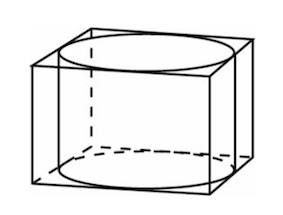
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.
Решение: + показать
Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
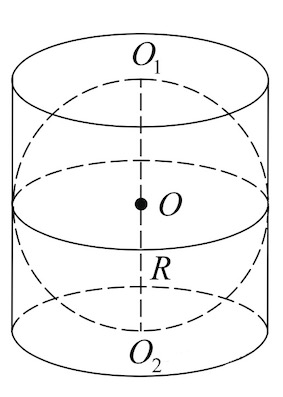
Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.
Решение: + показать
Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.
Решение: + показать
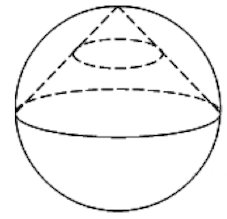
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.
Решение: + показать
Задача 12. Середина ребра куба со стороной является центром шара радиуса
Найдите площадь
части поверхности шара, лежащей внутри куба. В ответе запишите
Решение: + показать
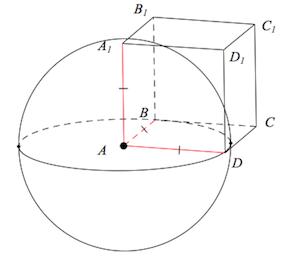
Задача 13. Вершина куба
со стороной
является центром сферы, проходящей через точку
. Найдите площадь
части сферы, содержащейся внутри куба. В ответе запишите величину
.
Решение: + показать
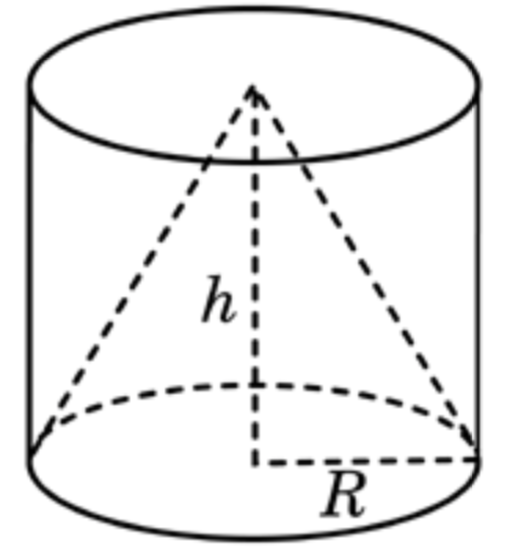
Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен
Решение: + показать
Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
Решение: + показать
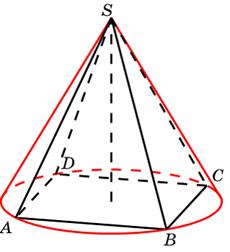
Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой
Найдите его объем, деленный на
.
Решение: + показать
Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Решение: + показать
Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.
Решение: + показать
Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и
Боковые ребра равны
. Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна
Решение: + показать
Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна
Решение: + показать
Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен
Решение: + показать
Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 26. Около куба с ребром описан шар. Найдите объем этого шара, деленный на
Решение: + показать
Задача 27. Куб вписан в шар радиуса Найдите объем куба.
Решение: + показать

(27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Дано:
ABCDA1B1C1D1 – призма, описанная
Ф – цилиндр, вписанный
ABCD – квадрат
AA1 ⊥ (ABC)
rц = Hц = 1
Найти:
S б п п
Решение:
1. Sб п п = Pо⋅H = 4⋅a⋅H
Т.к. цилиндр вписан в призму, то:
1. rц = Hц = 1
2. Основание цилиндра – круг – вписан в основание призмы – квадрат, т.е.
а = 2⋅r =2.
Итак, Sб п п = 4⋅2⋅1=8.
Ответ: 8.
(72973) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 5,5. Найдите площадь боковой поверхности призмы.
Дано:
ABCDA1B1C1D1 – призма, описанная
Ф – цилиндр, вписанный
ABCD – квадрат
AA1 ⊥ (ABC)
rц = Hц = 5,5
Найти:
S б п п
Решение:
(73005) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 15. Найдите площадь боковой поверхности призмы.
Площадь боковой поверхности призмы. Здравствуйте! В этой публикации мы с вами разберём группу задач по стереометрии. Рассмотрим комбинацию тел – призмы и цилиндра. На данный момент эта статья завершает всю серию статей связанных с рассмотрением типов заданий по стереометрии.
Если в банке заданий будут появляться новые, то, конечно же, будут и дополнения на блоге в будущем. Но и того что уже есть вполне достаточно, чтобы вы могли научиться решать все задачи с кратким ответом в составе экзамена. Материала хватит на годы вперёд (программа по математике статична).
Представленные задания связаны с вычислением площади боковой поверхности призмы. Отмечу, что ниже рассматривается прямая призма (и соответственно прямой цилиндр).
Без знания всяких формул, мы понимаем, что боковая поверхность призмы это все её боковые грани. У прямой призмы боковые грани это прямоугольники.
Площадь боковой поверхности такой призмы равна сумме площадей всех её боковых граней (то есть прямоугольников). Если речь идёт о правильной призме, в которую вписан цилиндр, то понятно, что все грани этой призмы являются РАВНЫМИ прямоугольниками.
Формально площадь боковой поверхности правильной призмы можно отразить так:
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Боковая поверхность данной призмы состоит из четырёх равных по площади прямоугольников. Высота грани равна 1, ребро основания призмы равно 2 (это два радиуса цилиндра), следовательно площадь боковой грани равна:
Площадь боковой поверхности:
Ответ: 8
73023. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √0,12, а высота равна 3.
Площадь боковой поверхности данной призмы равна сумме площадей трёх боковых граней (прямоугольников). Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота равна трём. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный треугольник в который вписана окружность с радиусом √0,12. Из прямоугольного треугольника АОС можем найти АС. А затем и AD (AD=2АС). По определению тангенса:
Значит AD=2АС=1,2.Таким образом, площадь боковой поверхности равна:
Ответ: 3,6
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √75, а высота равна 1.
Искомая площадь равна сумме площадей всех боковых граней. У правильной шестиугольной призмы боковые грани это равные прямоугольники.
Для нахождения площади грани необходимо знать её высоту и длину ребра основания. Высота известна, она равна 1.
Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный шестиугольник, в который вписана окружность радиуса √75.
Рассмотрим прямоугольный треугольник АВО. Нам известен катет ОВ (это радиус цилиндра). ещё можем определить угол АОВ, он равен 300 (треугольник АОС равносторонний, ОВ –биссектриса).
Воспользуемся определением тангенса в прямоугольном треугольнике:
АС=2АВ, так как ОВ является медианой, то есть делит АС пополам, значит АС=10.
Таким образом, площадь боковой грани равна 1∙10=10 и площадь боковой поверхности:
Ответ: 60
76485. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 8√3, а высота равна 6.
Площадь боковой поверхности указанной призмы из трёх равных по площади граней (прямоугольников). Чтобы найти площадь требуется знать длину ребра основания призмы (высота нам известна). Если рассматривать проекцию (вид сверху), то имеем правильный треугольник вписанный в окружность. Сторона этого треугольника выражается через радиус как:
Подробности этой взаимосвязи изложены здесь. Значит она будет равна
Тогда площадь боковой грани равна: 24∙6=144. А искомая площадь:
Ответ: 432
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Всё просто. Имеем четыре равных по площади боковые грани, следовательно площадь одной грани равна 48:4=12. Так как радиус основания цилиндра равен 2, то ребро основания призмы будет рано 4 – оно равно диаметру цилиндра (это два радиуса). Нам известна площадь грани и одно ребро, второе являющееся высотой будет равно 12:4=3.
Ответ: 3
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27170. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
Посмотреть решение
Как видите задачки на раз-два. На этом всё! Успеха вам!
С уважением, Александр.
Делитесь информацией в социальных сетях.