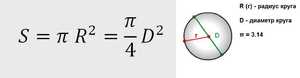Как найти площадь пробки

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a 2 + b 2 = c 2

Из нее можно вывести такую формулу:

c = S*q*r*t*(a 2 + b 2 )

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

где 2а – значение хорды, расчета площади поперечного сечения.

Источник

5.70 В вертикальную цилиндрическую трубку, снизу закрытую пробкой, наливают воду. Пробка с площадью поперечного сечения S = 8 см2 вылетает, когда масса воды становится равной т = 300 г. Чему равна площадь поперечного сечения трубки, если максимальная сила трения, действующая на пробку, равна F= 1,2 Н? Толщиной стенок трубки пренебречь.

Эту задачу можно решить двумя способами, исходя из силы F тяжести воды на дно трубки: F = mg = 0.3*10 = 3 H.

1) Поскольку сила давления на дно пропорциональна площади, то составим пропорцию:
3/1,2 = S/8.
Отсюда площадь S дна трубки равна: S = (3*8)/1.2 = 24/1.2 = 20 см².

2) Давление р на дно, при котором пробка вылетает равно:
р = F/S = 1.2/0.0008 = 1500 Па.
Из формулы р = F/S определяем S = F/p = 3/1500 = 0.002 м² = 20 см².

Знаешь ответ? Добавь его сюда!

Какую массу медного купороса CuSO4 5H2O и воды надо взять, чтобы приготовить раствор массой 500 г с массовой долей соли 5%?

Металлический цинк весом 26,2 г растворили в избытке раствора HCl. Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?

1. В окружности с центром О отрезки АС и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол АСВ. Ответ дайте в градусах.

а) Упростите данное выражение (12 баллов).

б) Найдите значение упрощённого выражения при b = 5 (5 баллов).

Вместо точек нежно вставить либо знаки + и — либо цифры

Помогите 2 часа сижу не могу здать дз

Найди значение выражения 75(k-11)-t(11-k), если k=2, t=25 числовое значение выражения равно

Разложи на множители x^3+5x^2-6x-30(x . . )(x^2 . . )на месте точек должны быть цифры или знаки + и —

Який об’єм карбон(IV) оксиду (н.у.) виділиться внаслідок спалювання 27,6 г. гліцеролу

Найти параллельные прямые и докажите их параллельность. Подскажите источник, откуда задачи

6.в каком произведение русской литературы действие происходит в местечке Княжье-Вено?кто его автор?

Продолжение боковых сторон АВ и CD трапеции ABCD пересекаются в точке Е. Найти площадь трапеции, если площадь треугольника ВЕС равна 33 см2 и EC : ED = 3:10

Task 4. Are these sentences true (T) or false (F)? Correct them.

1. Her name is Anna. She is doctor.

2. She has the flat in the London.

3. I go to the work by car.

4. We have the dinner at eight o’clock in the evening.

5. John always stays in bed late on Sunday mornings.

7. The students in this class aren’t lazy: they work hard.

8. Please, have a lunch with us!

9. What time do you go to the school?

10. Can I have an cheese sandwich, please?

11. What do you do in the evenings?

12. Have you finished reading a book I lent you?

13. The Ganges is a river which runs through India.

14. I would love to meet John in person.

15. She went to France by a train.

16. Jack’s mother is in the France on holiday.

17. Could you show me the way to Victoria Park, please?

18. I can meet you outside Hilton Hotel tonight at nine o’clock.

19. Where is the Kalahari Desert?

20. He is reading a book about the World War I.

21. Have you ever seen a Great Wall of China?

22. Let’s meet in Macey’s Restaurant.

23. He buys the Observer every morning.

24. They drove to the north of the England.

25. Can you please tell me a way to a nearest hospital?

26. People from United Kingdom are not only people who speak the English language.

28. They’re playing football on the beach.

29. I never drive to office. I always go on foot.

30. Which city in England is Tower Bridge located in?

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

iSopromat.ru

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.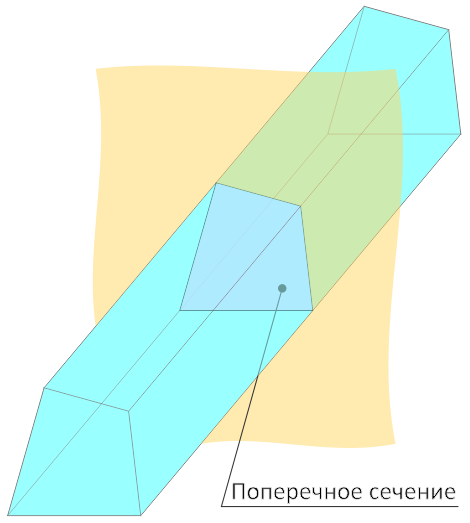

Сечение может иметь простую или сложную форму, а также быть составным.

Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.

Площадь поперечного сечения

В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.

Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:

Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:

Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м 2 , см 2 или мм 2 .

Площадь составного сечения

Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.

Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.

В результате сложив все составляющие профили, получим площадь всего сечения.

Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.

Длина поперечного сечения

Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.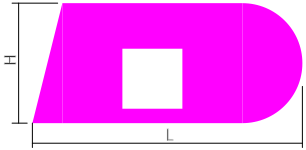

Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.

Ширина сечения определяется аналогично, но обозначается буквой H или h.

При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м 2 .

Различают два основных вида расчета площади сечений:

1. Геометрический — когда требуется найти площадь сечения тела по известным размерам;
2. Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.

Источник

Расчет площади поперечного сечения круга

В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

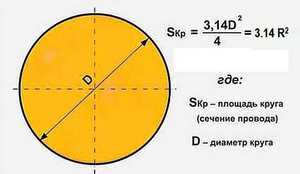
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

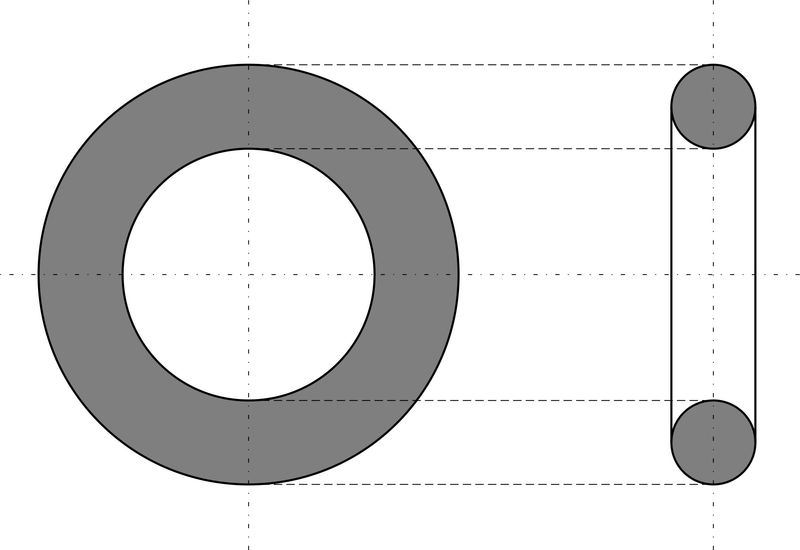
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Источник

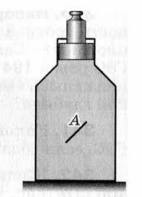
На пробку, вставленную в горлышко сосуда с водой (рис. 26), действует сила 2Н. Найдите силу давления на внутреннюю поверхность сосуда площадью 100

с

м

2

. Площадь сечения пробки 2

с

м

2

. Чему равны давление и сила давления на площадку А (S = 2

с

м

2

)? Силу тяжести воды не учитывать.

рис. 26

Общая площадь поверхности сферической крышки с учетом объема и отношения поверхности к объему Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	3D геометрия ↺
3D геометрия	Сферический колпачок ↺
Сферический колпачок	Площадь поверхности сферической крышки ↺
Площадь поверхности сферической крышки	Общая площадь поверхности сферической крышки ↺

Общая площадь поверхности сферической крышки с учетом объема и отношения поверхности к объему Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Отношение поверхности к объему сферической крышки: 1.1 1 на метр –> 1.1 1 на метр Конверсия не требуется
Объем сферической крышки: 440 Кубический метр –> 440 Кубический метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

484 Квадратный метр –> Конверсия не требуется

6 Общая площадь поверхности сферической крышки Калькуляторы

Общая площадь поверхности сферической крышки с учетом объема и отношения поверхности к объему формула

Общая площадь поверхности сферической крышки = Отношение поверхности к объему сферической крышки*Объем сферической крышки

TSA = R_A/V*V

Что такое сферическая крышка?

В геометрии Сферический колпак или сферический купол — это часть сферы или шара, отсеченная плоскостью. Это также сферический сегмент одного основания, т. е. ограниченный одной плоскостью. Если плоскость проходит через центр сферы, так что высота шапки равна радиусу сферы, то Сферическая шапка называется полусферой.

Перейти к содержимому Меню Закрыть

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Знания.ком

Меню

Знания.ком

Искать:

Меню

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Кнопка