Как найти площадь проекции прямоугольника

Как найти площадь проекции прямоугольника

Параллельное проецирование. Площадь проекции фигуры

В задачах по геометрии успех зависит не только от знания теории, но и от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.

Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.

Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.

Параллельное проецирование

Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:

Проекцией отрезка будет отрезок.

Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.

Проекцией круга в общем случае окажется эллипс.

Проекцией прямоугольника — параллелограмм.

Вот как выглядит проекция куба на плоскость:

Здесь передняя и задняя грани параллельны плоскости проекции

Можно сделать по-другому:

Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.

Рисуем проекции пирамиды,

цилиндра:

и шара:

Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.

Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.

Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.

Площадь проекции фигуры

В следующей статье рассказано, как выбрать наиболее удачный ракурс для построения чертежей в задачах по стереометрии, а также о распространенных ошибках, которые могут помешать решению.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Параллельное проецирование. Площадь проекции фигуры» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

19
Фев 2014

Категория: Справочные материалы

Площадь ортогональной проекции многоугольника

2014-02-19
2014-02-19

Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.

Доказательство:

7

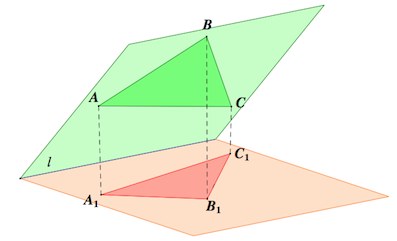
Пусть  треугольник A_1B_1C_1 – проекция  треугольника ABC на проецируемую плоскость.

Докажем, что

S_{A_1B_1C_1}=S_{ABC}cdot cosalpha,

где alpha – угол между плоскостями ABC,;A_1B_1C_1

Для этого разобьем треугольник  ABC на два треугольника c общей стороной AM, параллельной прямой l пересечения плоскостей ABC,;A_1B_1C_1. (Частный случай, когда одна из сторон треугольника ABC параллельна линии пересечения плоскостей l, можно рассмотреть отдельно (самостоятельно)).

г

Проекция треугольника ABM –   треугольник A_1B_1M_1. Причем AM=A_1M_1.

Пусть BH – перпендикуляр к l. Тогда по т. о трех перпендикулярах и B_1H – перпендикуляр к l.  Стало быть, angle BHB_1=alpha – угол между плоскостями треугольников (проецируемого и проекции).

Пусть T – точка пересечения BH и AM, T_1 – проекция т. T на плоскость A_1B_1C_1. Очевидно, BT – высота треугольника ABM (B_1T_1 – высота треугольника A_1B_1M_1).

Из треугольника BHB_1

cosalpha =frac{B_1H}{BH}

Но и

frac{HT_1}{HT}=cosalpha

Тогда BT=BH-HT=frac{1}{cosalpha }(BH_1-HT_1)=frac{B_1T_1}{cosalpha}.

Имеем: S_{ABM}=frac{1}{2}BTcdot AM=frac{1}{2}cdot frac{B_1T_1}{cosalpha}cdot AM=frac{S_{A_1B_1M_1}}{{cosalpha}}.

Аналогичные рассуждения – для пары треугольников AMC и A_1M_1C_1:

hj

S_{AMC}=frac{1}{2}CRcdot AM=frac{1}{2}cdot frac{C_1R_1}{cosalpha}cdot AM=frac{S_{A_1M_1C_1}}{{cosalpha}}

(где CR – высота треугольника ACM, C_1R_1 – ее проекция)

Итак, суммируя площади треугольников ABM,;ACM и A_1B_1M_1,;A_1C_1M_1 соответственно, получаем

S_{ABC}=frac{S_{A_1B_1C_1}}{cosalpha}

или

S_{A_1B_1C_1}=S_{ABC}cdot cosalpha

Что и требовалось доказать.

Пример. 

Ребро куба равно 2 см. Через диагональ основания под углом 45^{circ} к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Решение:

площадь ортогональной проекции

Пусть плоскость сечения проведена через диагональ BD и пересекает боковое ребро  (CC_1) в точке T.

По вышеуказанной теореме

S_{BDT}=frac{S_{BCD}}{cosalpha},

где треугольник BCD – проекция треугольника BTD на плоскость основания, alpha – угол между плоскостями BCD,;BTD.

S_{BDT}=frac{2}{frac{sqrt2}{2}}=2sqrt2.

Ответ: 2sqrt2.

Применение теоремы можно также посмотреть, например, в этой задаче.

Автор: egeMax |

Нет комментариев

Печать страницы

Источник

Определение 1.

Проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на плоскость, если точка не лежит в данной плоскости, и сама данная точка, если она лежит в этой плоскости. 

Определение 2.

Фигура, состоящая из проекций всех точек фигуры на некоторую плоскость, называется проекцией фигуры на эту плоскость.

Теорема. Площадь проекции плоской фигуры на плоскость ω равна произведению площади фигуры на косинус угла между плоскостью фигуры и плоскостью ω.

Источник

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

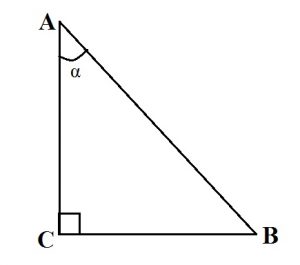
прямоугольный треугольник формулы

  1. Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
  2. Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
  3. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.  AB2 = AC2 + CB2

Прямоугольный треугольник:  формулы площади и проекции

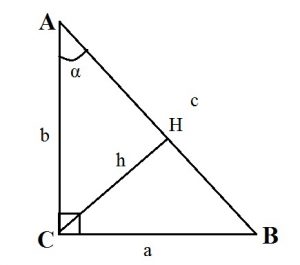
Прямоугольный треугольник формулы

  1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
  2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH2 = AH·BH.
  3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое  между гипотенузой и проекцией этого катета на гипотенузу:  CA2 = AB·AH;  CB2 = AB·BH.
  4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
  5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
  6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты.  S = (hc):2.

Прямоугольный треугольник:  формулы тригонометрия

  1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.                 cosα  = AC: AB.
  2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.           sinα = BC:AB.
  3. Тангенс  острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.    tgα  = BC:AC.
  4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.    ctgα  = AC:BC.
  5. Основное тригонометрическое тождество:  cos2α + sin2α = 1.
  6. Теорема косинусов: b2 = a2 + c2 – 2ac·cosα.
  7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник:  формулы для описанной окружности

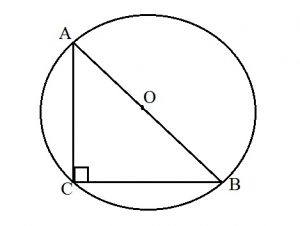
прямоугольный треугольник формулы

  1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
  2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник:  формулы для вписанной  окружности

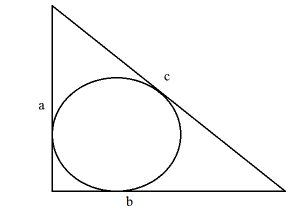
прямоугольный треугольник формулы

Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b  -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из  сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

Решение:

  1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
  2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Ответ: AB = 28.

ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)

Источник

Как найти площадь поверхности?

Умножьте длину и ширину или c и b, чтобы найти их площадь. Умножьте это измерение на два, чтобы учесть обе стороны. Сложите три отдельных измерения вместе. Поскольку площадь поверхности – это общая площадь всех граней объекта, последний шаг – сложить вместе все индивидуально рассчитанные площади.

Для измерения внутреннего объема:

  1. Для открытой детали щелкните Пересечение (панель инструментов “Элементы”) или выберите Вставка > Элементы > Пересечение.
  2. В дереве конструирования FeatureManager выберите Shell1 и Plane6.
  3. Щелкните Пересечение (панель инструментов “Элементы”) или Вставка > Элементы > Пересечение.
  4. В PropertyManager щелкните Создать внутренние области и щелкните Пересечение.

Как найти площадь поверхности квадрата?

Как найти площадь квадрата – формулы. Площадь квадрата равна произведению длины его сторон: площадь = а * а = а², где а — сторона квадрата.

Что такое единица площади?

Площадь — это площадь поверхности, которую может покрыть двумерная фигура, измеряемая в квадратных единицах. Единицей площади СИ является квадратный метр (м2), которая является производной единицей.

Как вычислить площадь проекции?

Расчет площади проекции

Если ветер дует перпендикулярно квадратной или прямоугольной поверхности, площадь рассчитывается как площадь, равная длине, умноженной на ширину (A=LH). Для стены длиной 20 футов и высотой 10 футов площадь проекции равна 20 × 10 или 200 квадратных футов.

Как найти площадь проекции цилиндра?

Формулы цилиндра в единицах r и h:

  1. Вычислить объем цилиндра: V = πr2h.
  2. Вычислите площадь боковой поверхности цилиндра (только изогнутой снаружи) **: L = 2πrh.
  3. Вычислите площадь верхней и нижней поверхности цилиндра (2 круга): T = B = πr. …
  4. Общая площадь закрытого цилиндра составляет:

Какая формула объема?

В то время как основная формула для площади прямоугольной формы – длина × ширина, основная формула для объема – длина × ширина × высота.

Как мне отрегулировать громкость?

Высота × ширина × глубина = объем

Если высота, ширина и глубина измеряются в см, ответ будет см³.

Какова формула площади всех форм?

Периметр, площадь и объем

Таблица 2. Формулы площади
Форма Формула Переменные
Квадратный А = s2 s – длина стороны квадрата.
Прямоугольные A = LW L и W – длины сторон прямоугольника (длина и ширина).
Треугольник A = 12bh b и h – основание и высота

Какова площадь квадрата 4 см?

Рассмотрим квадрат, длина стороны которого равна 4 см. Методом подсчета квадратов находим, что площадь квадрата равна 16 см.2.

Чему равна площадь прямоугольника?

Другими словами, площадь прямоугольника равна произведению его длины на ширину. То есть A = lxw, где l — длина, а w — ширина прямоугольника. Например, площадь прямоугольника длиной 35 м и шириной 25 м равна 35 умножить на 25 или 875 квадратных метров.

Источник

Добавить комментарий