Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза
1. Если известны только катеты
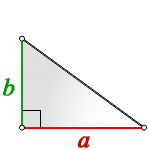
a, b – катеты треугольника
Формула площади треугольника через катеты ( S ) :
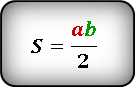
2. Если известны острый угол и гипотенуза или катет
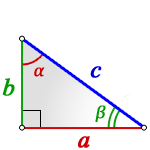
c – гипотенуза
a, b – катеты
α, β – острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
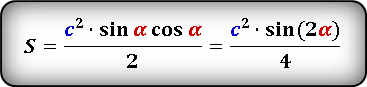
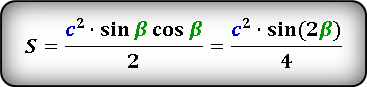
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
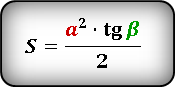
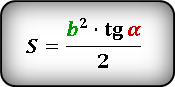
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
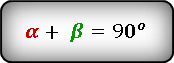
то справедливы следующие тождества:
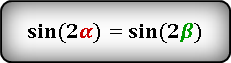
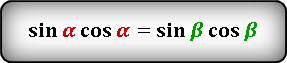
3. Если известны радиус вписанной окружности и гипотенуза
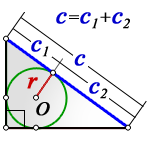
c – гипотенуза
c1, c2 – отрезки полученные делением гипотенузы, точкой касания окружности
r – радиус вписанной окружности
О – центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
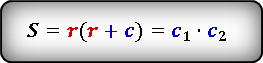
- Подробности
-
Опубликовано: 07 сентября 2011
-
Обновлено: 13 августа 2021
Площадь прямоугольного треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Площадь прямоугольного треугольника по двум катетам
- Площадь прямоугольного треугольника по катету и гипотенузе
- Площадь прямоугольного треугольника по гипотенузе и углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь прямоугольного треугольника по катету и противолежащему углу
- Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Площадь прямоугольного треугольника по двум катетам
Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.
На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:
Пример 1. Известны катеты прямоугольного треугольника: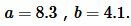 
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения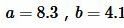 
в (1), получим:
Ответ: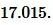 
Площадь прямоугольного треугольника по катету и гипотенузе
Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):
Найдем площадь треугольника. Из формулы Пифагора имеем:
Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:
Пример 2. Известны катет и гипотенуза прямоугольного треугольника: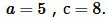 
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значения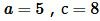 
в (3), получим:
Ответ: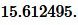 
Площадь прямоугольного треугольника по гипотенузе и углу
Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):
Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:
или
Подставим (4) в (1):
Из формулы произведения тригонометрических функций имеем:
Подставим в (6) ( small beta=alpha ):
Применяя (7) относительно формулы (5), получим:
Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: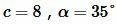 
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения 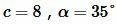в (8), получим:
Ответ: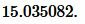 
Площадь прямоугольного треугольника по катету и прилежащему углу
Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):
Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:
Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: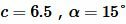 
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения 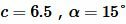в (10), получим:
Ответ: 
Площадь прямоугольного треугольника по катету и противолежащему углу
Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):
Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:
Откуда
Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:
Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: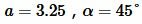 
. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения 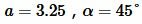в (13), получим:
Ответ: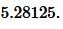 
Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис.6):
Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.
Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку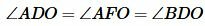 
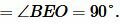Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):
Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):
Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:
Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:
Подставляя (16), (17) в (18), получим:
или
Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: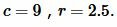 
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения 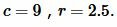в (19), получим:
Ответ: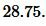 
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность
Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис.6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:
Учитывая, что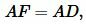 
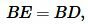
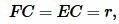
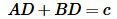, (20) примет вид:
То есть
Сравнивая формулы (19) и (21) можем записать:
Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:
Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6)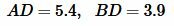 
Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения 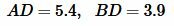в (22), получим:
Ответ: 
Смотрите также:
- Площадь треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
Какие размеры известны:
Два катета
Катет и гиппотенуза
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Треугольник – это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.
Треугольники бывают прямоугольный, равнобедренный, равносторонний.
Катет – это прилежащая прямому углу сторона треугольника.
Гипотенуза – это сторона треугольника противолежащая прямому углу.
Формула площади прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника, необходимо знать размеры двух сторон треугольника.
Площадь прямоугольного треугольника расчитывается по формуле:
a
b
c
S = dfrac{a cdot b}{2}
- S – площадь треугольника
- a – катет
- b – катет
- c – гипотенуза
Если известены размеры только одного катета и гипотенузы, тогда площадь прямоугольного треугольника можно расчитать по формулам:
S = dfrac{a cdot sqrt{c^2 – a^2}}{2}
S = dfrac{b cdot sqrt{c^2 – b^2}}{2}
Похожие калькуляторы:
Войдите чтобы писать комментарии
Площадь прямоугольного треугольника – это далеко не самая сложная тема по математике, но все же она нередко вызывает вопросы у школьников. В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы.
Математические определения
Прямоугольный треугольник – это тот, один из углов которого является прямым, то есть равен 90 градусам. Чтобы научиться находить площадь этой фигуры, сначала нужно запомнить следующие определения:
- гипотенуза – это сторона, которая противоположна прямому углу.
- катеты – это две стороны, которые прилегают к прямому углу.
- высота – это линия, которая проведена от угла к противоположной ему стороне под прямым углом. В прямоугольном треугольнике две высоты совпадают с его катетами.
Формулы определения площади прямоугольного треугольника
Для нахождения площади этого треугольника можно использовать разные формулы в зависимости от того, какие данные даются в задаче.
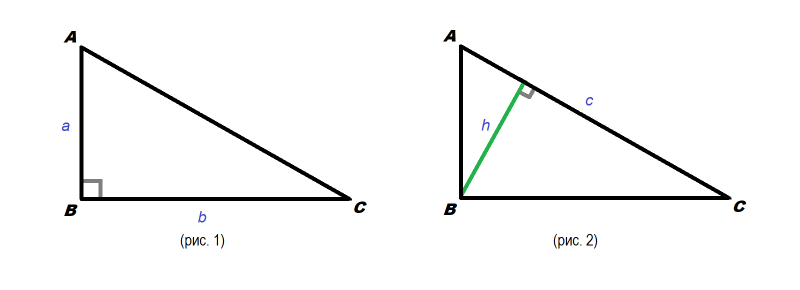
Если известны:
- оба катета, то следует найти их произведение и разделить на два (рис. 1): S= (a*b)/2. Прямоугольный треугольник – это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)
- гипотенуза и проведенная к ней из прямого угла высота, то найти площадь можно, умножив их друг на друга и разделив на два (рис. 2): S= (c*h)/2.
Задачи для тренировки
Теперь нужно закрепить знания и научиться находить площадь прямоугольного треугольника по формулам, которые мы рассмотрели ранее. Для этого рассмотрим две типовые задачи:
Задача №1 (рисунок 1). Известно, что у треугольника ABC c ∠ABC = 90° сторона AB = 3 см, а BC = 6 см. Нужно найти площадь этой фигуры.
Нам нужно воспользоваться первой из ранее рассмотренных формул и найти половину от произведения катетов: (3*6)/2 = 9 см².
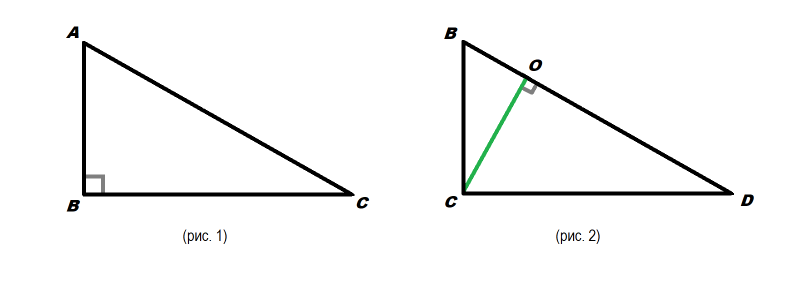
Задача №2 (рисунок 2). Из прямого угла в треугольнике BCD проведена высота BO = 4 дм, а сторона BD = 8 дм. Чему будет равна S?
В этом случае воспользуемся второй по счету формулой, и с ее помощью найдем половину от произведения гипотенузы и высоты: (4*8)/2 = 16 дм².
Курсы по математике
Тема, рассмотренная в данной статье, является лишь одной из многих, которые детям предстоит освоить. Математика включает в себя широкий комплекс знаний, и чтобы хорошо знать этот предмет, школьникам нужно не только последовательно проходить материал, но и дополнительно развивать свои математические способности.
Помочь справиться с этой задачей может курс по математике для учеников 1-4 классов Амаматика от академии развития интеллекта AMAkids. На занятиях ребята не только расширят свои математические знания, но и познакомятся со смежными областями математики. Благодаря использованию развивающих игр и различных интерактивных материалов дети с интересом будут развивать свои способности – логику, мышление, креативность.
Запишитесь на курс Амаматика и начните развивать навыки ребенка уже сейчас!
