Как найти площадь прямоугольник через диагонали

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

S — искомая площадь прямоугольника;
a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

S — искомая площадь прямоугольника;
a — известная сторона;
R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

S — искомая площадь прямоугольника;
a — известная сторона;
P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

S — искомая площадь прямоугольника;
d — любая диагональ прямоугольника;
α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

S — искомая площадь прямоугольника;
R — радиус описанной окружности;
α — любой угол между диагоналями прямоугольника.

Калькулятор площади прямоугольника

Рассчитайте онлайн площадь прямоугольника, зная его стороны или диагонали.

Что известно

Размерность

Сторона 1

см

Сторона 2

см

Диагональ

см

Угол

гр.

Раcсчитать

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

🧮 Калькулятор для расчета площади прямоугольника

Калькулятор площади прямоугольника — это онлайн инструмент, который помогает вычислить площадь прямоугольника. Для вычисления площади прямоугольника необходимо умножить длину на ширину. Формула вычисления площади прямоугольника:

S = a x b

где S – площадь прямоугольника, a – длина прямоугольника, b – ширина прямоугольника.

Калькулятор площади прямоугольника обычно позволяет ввести значения длины и ширины прямоугольника и автоматически вычисляет его площадь. Это может быть полезно для решения задач по геометрии или при необходимости быстрого расчета площади прямоугольной поверхности.

С нашим калькулятором площадь прямоугольника можно рассчитать не только используя значение длины и ширины, но и через диагонали и угол между ними. Формула будет выглядеть следующим образом:

S = 0,5 × d² × 𝑠𝑖𝑛(𝑎)

где S – площадь прямоугольника, d – длина диагоналей прямоугольника, α – угол между диагоналями.

Для чего можно использовать такой калькулятор?

Калькулятор площади прямоугольника может быть полезен в различных ситуациях, например:

При решении задач по геометрии, связанных с прямоугольниками.
При выполнении строительных работ, когда необходимо вычислить площадь прямоугольного участка земли или поверхности для проведения работ.
При работе в области дизайна интерьера и мебели, где необходимо вычислить площадь прямоугольных поверхностей для расчета материалов или определения размеров мебели.
В учебных целях, чтобы лучше понимать связь между диагоналями, углами и площадью прямоугольника.

Калькулятор площади прямоугольника может значительно упростить и ускорить процесс вычисления площади.

Пример

Допустим, у вас есть комната прямоугольной формы, и вы хотите вычислить ее площадь для того, чтобы определить количество краски, необходимое для ее покраски.

Для этого необходимо измерить длину и ширину комнаты с помощью измерительной ленты. Предположим, что длина комнаты составляет 6 метров, а ширина – 4 метра.

Затем можно воспользоваться калькулятором площади прямоугольника, введя значения длины и ширины комнаты в соответствующие поля. Калькулятор автоматически вычислит площадь комнаты, которая в данном случае составляет 24 квадратных метра.

Таким образом, зная площадь комнаты, можно определить, сколько краски понадобится для ее покраски, используя информацию о расходе краски на квадратный метр поверхности. Такой расчет может быть полезен, если вы собираетесь сделать ремонт в своей квартире или доме.

❓Вопросы и ответы

Несколько вопросов и ответы на них по калькулятору площади прямоугольника:

Что такое площадь прямоугольника?

Площадь прямоугольника — это мера, определяющая, сколько плоской поверхности занимает данный прямоугольник.

Для чего нужен калькулятор площади прямоугольника?

Калькулятор площади прямоугольника может использоваться во многих ситуациях, например, при строительных работах, в дизайне интерьера, при решении задач по геометрии и в повседневной жизни.

Что такое диагональ прямоугольника?

Диагональ прямоугольника — это отрезок, соединяющий противоположные вершины прямоугольника.

Что такое прямоугольник?

Прямоугольник — это геометрическая фигура, которая имеет четыре угла, все из которых прямые (равны 90 градусам), и противоположные стороны параллельны друг другу и имеют равные длины.

По определению, прямоугольник является частным случаем параллелограмма, у которого все углы прямые.

Можно ли использовать такой калькулятор для измерения площади других четырехугольников?

Нет, калькулятор площади прямоугольника может быть использован только для измерения площади прямоугольника, который имеет две параллельные стороны и все углы равны 90 градусов.

Для измерения площади других четырехугольников, таких как квадрат, ромб, трапеция, параллелограмм или прямоугольная трапеция, необходимо использовать соответствующий калькулятор для каждой фигуры, который учитывает специфические формулы и свойства этих фигур.

Онлайн-калькулятор площади прямоугольника

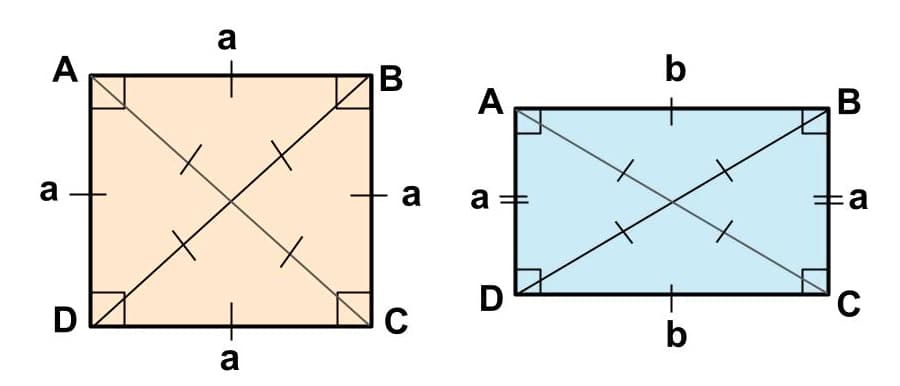
Вначале давайте разберемся с определением. У прямоугольника есть 4 стороны. Каждая сторона равна противоположной и параллельна ей. Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.

Все 4 угла, находящиеся внутри прямоугольника, — прямые. То есть каждый угол равен 90°.

Формула площади прямоугольника через его стороны

Чтобы найти площадь SS прямоугольника, нужно перемножить две его стороны: сторону aa умножаем на сторону bb.

S=a⋅b.S = a cdot b.

Пример

У нас есть прямоугольник ABCDABCD. Одна его сторона ABAB равна 55 см, вторая BCBC равна 33 см. Нам нужно найти его площадь SS.

Решение:

Чтобы найти площадь SS, нужно умножить сторону ABAB на сторону BCBC и получаем: S=5⋅3S = 5 cdot 3.

Ответ: S=15S = 15 см².

Формула площади прямоугольника через диагонали

Площадь прямоугольника можно также рассчитать, зная длину диагоналей и острый угол между ними:

S=12d2sin⁡α.S = frac {1}{2}d^2 sin alpha.

Помним, длины диагоналей в прямоугольнике равны и при пересечении делятся пополам.

Пример

Дан прямоугольник ABCDABCD. Его диагональ ACAC равна 88 см, а острый угол между диагоналями 30°30°. Найдите площадь фигуры.

Используем приведенную выше формулу и получаем:
S=12⋅82⋅sin⁡30∘=12⋅64⋅12=644=16S = frac{1}{2} cdot 8^2 cdot sin 30^{circ} = frac{1}{2} cdot 64 cdot frac{1}{2} = frac{64}{4} = 16

Ответ: S=16S = 16 см².

Не знаете, как решить задачу по геометрии онлайн? Оформите заказ на Студворк!

Тест по теме «Площадь прямоугольника»

Источник

Download Article

When you’re working with rectangles, you can find out a lot of information about them just by knowing a few key points of information. If you’ve been given the length of the diagonal and at least one side, you can calculate the area of the whole shape with just a few equations. Always use a calculator to check your math, and don’t forget to add your units onto the answer!

1
Mark the diagonal on the rectangle. If you have a visual of your rectangle, it will be a lot easier to figure out the area given a diagonal. Draw out a rectangle (it doesn’t have to match the proportions given, just a rectangle shape will do) and mark out a diagonal line to create 2 triangles.^[1]
- You’ll be able to see the 2 triangles that make up the rectangle now.
2

Advertisement
3
4
5

Plug the new number into . To find the area of your entire rectangle, you need to solve for Area = length x width, or A = l x w. Now that you’ve used the Pythagorean Theorem to find the second side length, you can solve for the area. Don’t forget your units!^[5]

1
Mark the diagonal and side length on your rectangle. If you have a visual in front of you, it will be much easier to see how you’re solving your equation. Draw a simple rectangle with a ruler and create a diagonal line across it to make 2 triangles.^[6]
- It’s not mandatory to draw your triangle, but it can help you, especially if you’re just starting out.
2
Enter the length and diagonal into ${displaystyle A=ltimes {sqrt {d^{2}-l^{2}}}}$ . Simply plug the length and the diagonal into the formula above. Remember, the diagonal is always longer than the length of the rectangle. ^[7]
- For example, if the length is 8 inches and the diagonal is 10 inches, the formula would be ${displaystyle A=8times {sqrt {10^{2}-8^{2}}}}$ .
3

Add New Question

Question

If the diagonal of a rectangle is10cm then what is its area?

You don’t have enough information to solve.
Question

A rectangle with diagonal of 20 cm has sides in the ratio 2:1. How do I find the area of rectangle?

Such a rectangle would have its sides and diagonal in the ratio of 2:1:√5 (per the Pythagorean theorem). The ratio of √5 to the diagonal (20) is equal to the ratio of 2 to the longer side (or the ratio of 1 to the shorter side). Thus √5 : 20 = 2 : x, where x is the longer side. Expressed as fractions, that’s √5 / 20 = 2 / x. Cross-multiplying: (√5)(x) = (20)(2). Dividing by √5: x = 40 / √5 = 40 / 2.236 = 17.9 cm. The shorter side is half that, or 8.94 cm.
Question

If the side = 48 meters and the diagonal = 50 meters, how do I find the area of the rectangle?

Let s be the shorter side. Then (by the Pythagorean Theorem) s² + 48² = 50². So s² + 2304 = 2500. Then s² = 196, and s = 14 m. The area is 48 x 14 = 672 square meters.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

If all you know is the length of the diagonal, you can calculate the area of a square, but not a rectangle.
To find the area of a rectangle, you need to know the diagonal and at least one side length.
You can also use an online calculator, like Omni Calculator, to check your work.

1. Если известны две соседние стороны

2. Если известны любая сторона и диагональ

3. Если известны любая сторона и диаметр описанной окружности

4. Если известны любая сторона и радиус описанной окружности

5. Если известны любая сторона и периметр

6. Если известны диагональ и угол между диагоналями

7. Если известны радиус описанной окружности и угол между диагоналями

Калькулятор площади прямоугольника

🧮 Калькулятор для расчета площади прямоугольника

Для чего можно использовать такой калькулятор?

Пример