-
Главная
-
ГДЗ
- 3 класс
- Математика
-
Моро учебник
- Деление нуля на число
- Страница 87. Часть 1
Вернуться к содержанию учебника
Деление нуля на число
Вопрос
7. Реши уравнения.
| 75 + x = 90 | 80 – k = 42 | 6 • n = 54 |
Подсказка
Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.
Ответ
Вопрос
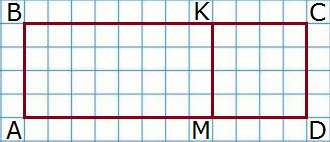
8. 1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.
Подсказка
Чтобы найти площадь прямоугольника ABCD, нужно сложить площади прямоугольников ВСКЕ и AEKD или измерить стороны прямоугольника ABCD и умножить длину на ширину.
Ответ
Вопрос
9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD – и на сколько квадратных сантиметров.
Подсказка
Площадь прямоугольника равна произведению его длины и ширины.
Ответ
Вопрос
На сколько 9 меньше, чем 72?
Во сколько раз 6 меньше, чем 54?
Подсказка
Чтобы узнать, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее – вычитание.
Чтобы узнать, во сколько раз одно число больше или меньше другого, нужно узнать, сколько раз маленькое число содержится в большом – деление.
Ответ
Вопрос
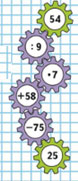
Цепочка:
Подсказка
Ответ
Вернуться к содержанию учебника
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 1. Страница 86. Номер №8
Решение 1
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
.
Решение 2
Способ 1.
AB = CD = 5 см;
BC = AD = 2 см;
S
A
B
C
D
=
A
B
∗
A
D
=
5
∗
2
=
10
(
с
м
2
)
.
Способ 2.
BC = EK = AD = CK = BE = 2 см;
KD = EA = 3 см;
S
B
C
K
E
=
B
C
∗
C
K
=
2
∗
2
=
4
(
с
м
2
)
;
S
A
E
K
D
=
E
K
∗
K
D
=
2
∗
3
=
6
(
с
м
2
)
;
S
A
B
C
D
=
S
B
C
K
E
+
S
A
E
K
D
=
4
+
6
=
10
(
с
м
2
)
.
- 02
Янв 18
Числа от 1 до 100 (продолжение)
Внетабличное умножение и деление
19. 1) Для детского сада купили 6 красных шаров и 3 синих, по цене 5 р. за каждый. Сколько денег заплатили за все эти шары?
Реши задачу двумя способами, составляя выражения.
1-й способ 2-й способ
6 • 5 + 3 • 5 = 45 (р.) (6 + 3) • 5 = 45 (р.)
О т в е т: заплатили 45 р. О т в е т: заплатили 45 р.
2) Запиши и объясни, как можно найти площадь прямоугольника ABCD, умножая сумму на число, и как можно найти его площадь другим способом.
Сторона BC состоит из отрезков BK и KC. Аналогично, сторона AD состоит из отрезков AM и MD. Причём, BK = AM = 4 см, а KC = MD = 2 см. AB = MK = DC = 2 см. Тогда, площадь прямоугольника ABCD равна: (BK + KC) • AB = (4 + 2) • 2 = 12 см2.
Можно представить площадь прямоугольника ABCD в виде суммы площадей прямоугольника ABKM и квадрата MKCD: 4 • 2 + 2 • 2 = 12 см2.
3) Вычисли значения выражений любым способом.
(3 + 6) • 4 = 9 • 4 = 36
(5 + 8) • 5 = 5 • 5 + 8 • 5 = 25 + 40 = 65
3 • (7 + 2) = 3 • 9 = 27
ГДЗ по математике. Рабочая тетрадь. 3 класс. Часть 2. Моро М. И., Волкова С. И.
Математика. 3 класс
3 класс. Рабочая тетрадь №2. Ответы к стр. 10
4 (80.93%) от 410 голосующих
Здравствуйте-здравствуйте! Ну, вот мы и опять
свиделись.
В прошлый раз я рассказал вам о том, что такое
площадь. Помните, как в книге это говорится:
Площадь – это часть плоскости,
ограниченная замкнутой кривой или ломаной линией.
А еще я рассказал вам, как можно сравнить
площади разных фигур – на «глазок» или наложив одну фигуру на другую. Но
лучше всего, конечно, сначала узнать площадь фигур, а потом сравнить полученные
результаты.
На прошлом уроке мы находили площадь фигур,
укладывая по всей их площади квадратные сантиметры. Получалось, как будто пол
квадратной плиткой выложили. Сколько плиточек – квадратных сантиметров
– такова и площадь фигуры. Конечно, так можно находить площадь, но это довольно
долго и не совсем удобно. Но моя волшебная математическая книга предлагает
другой, более короткий способ нахождения площади, если надо найти площадь
прямоугольника.
Итак, вот перед вами прямоугольник со сторонами 5 см
и 3 см. Проведём в нем горизонтальные и вертикальные линии, расстояние между
которыми – один сантиметр. Получилось, что вся площадь прямоугольника
как бы разделена на квадратные сантиметры. Посчитаем, сколько таких квадратных
сантиметров в первом ряду – один, два, три, четыре, пять. Во втором ряду тоже
пять и в третьем – так же пять. По пять квадратных сантиметров три раза находим
действием умножения. Получается, что площадь этого прямоугольника
равна пятнадцати квадратным сантиметрам.
5 · 3 = 15 (см2)
Ответ: площадь прямоугольника 15 см2 .
Ну, а если посчитать по-другому? В первом
столбике квадратных сантиметра, во втором тоже три, и в третьем, и в четвёртом,
и в пятом. По три квадратных сантиметра пять раз. Всё равно получилось, что площадь
прямоугольника равна пятнадцати квадратным сантиметрам.
3 · 5 = 15 (см2)
Ответ: площадь прямоугольника 15 см2.
А теперь давайте найдем площадь вот
этого прямоугольника. Длина равна шести сантиметрам, ширина –
четырем сантиметрам. Делим его на квадратные сантиметры.
Получается, по шесть квадратных сантиметров четыре
раза или по четыре квадратных сантиметра шесть раз. И так, и этак, площадь
этого прямоугольника равна двадцати четырем квадратным сантиметрам.
6 · 4 = 24 (см2) 4 · 6 = 24 (см2)
Ответ: площадь прямоугольника 24 см2 .
А вы обратили внимание, когда находили площадь первого
прямоугольника, мы перемножали числа пять и три. А эти числа являются длиной
и шириной нашего прямоугольника. А когда находили площадь второго
прямоугольника, перемножали числа шесть и четыре. Они тоже являются его длиной
и шириной. Значит, можно сделать вывод:
Чтобы найти площадь прямоугольника,
надо измерить длину и ширину этого прямоугольника и найти произведение
полученных чисел.
Вот, к примеру, длина прямоугольника равна восьми
сантиметрам, а ширина – четырём.
Площадь мы находим, умножив длину на ширину.
Произведение чисел восемь и четыре равно тридцати
двум. Значит, площадь этого прямоугольника равна
тридцати двум квадратным сантиметрам. Не забудьте, что площадь измеряется
именно в квадратных единицах. В нашей задаче это квадратные сантиметры. И
справа от сокращенного см обязательно пишем чуть выше маленькую двоечку.
А для того, чтобы легче было запомнить, как находить
площадь прямоугольника, можно записать памятку-формулу:
S = a
· b, где S
это площадь, а а и b
стороны прямоугольника.
А вот теперь я хочу предложить вам вот такую задачу.
Площадь прямоугольника равна восемнадцати квадратным сантиметрам, а ширина
его – два сантиметра. Чему равна длина этого прямоугольника?
И вот тут-то на помощь нам придёт формула S
= a · b.
Площадь
– это произведение, длина и ширина – множители. В задаче надо найти длину, то
есть множитель. А ведь мы знаем правило: Чтобы найти неизвестный
множитель, надо произведение разделить на известный множитель.
Частное чисел восемнадцать и два равно девяти.
Значит, длина этого прямоугольника равна девяти сантиметрам.
18 : 2 = 9 (см)
Ответ: длина прямоугольника равна 9 см.
Ну, а если необходимо найти ширину прямоугольника,
как например, вот в этой задаче?
Чему равна ширина прямоугольника, если его площадь –
12 см2, а длина – 4 см?
Конечно так же, как и длину – делением. Ведь ширина
в нашей формуле тоже является неизвестным множителем. Двенадцать делим
на четыре, получается три. В этом прямоугольнике ширина равна трем сантиметрам.
12 : 4 = 3 (см)
Ответ: длина прямоугольника равна 3 см.
Ну вот и пришла пора нам с вами сегодня расстаться.
Но я надеюсь, что вы хорошо усвоили, что:
Чтобы найти площадь прямоугольника
надо его длину умножить на ширину.
Чтобы найти неизвестную сторону прямоугольника,
если известна его площадь и вторая сторона, надо площадь разделить на известную
сторону.
Ну и, конечно, не забывайте, что площадь измеряется
в квадратных единицах измерения. Пока я познакомил вас только с
квадратными сантиметрами (1 см2, 15 см2 , 24 см2).
Но очень скоро вы познакомитесь и с другими единицами измерения площади. А я прощаюсь
с вами, буду дальше читать эту интересную книгу. До свидания, ребята.