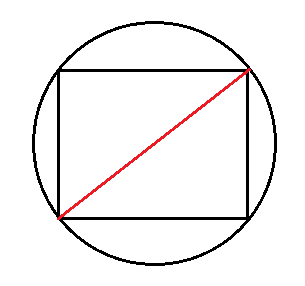
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
11 423

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
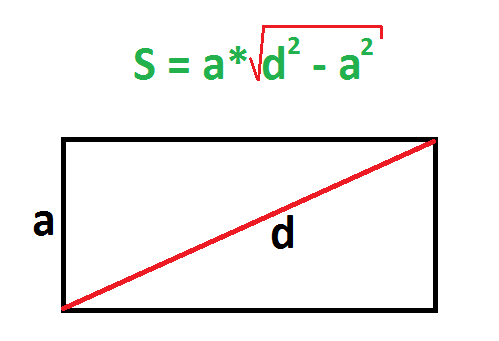
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
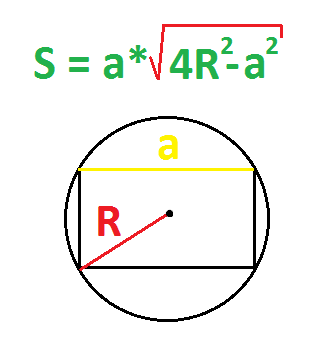
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
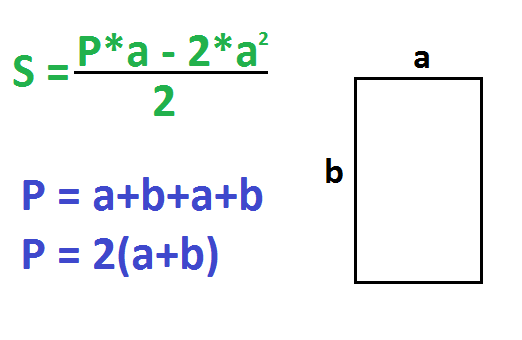
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
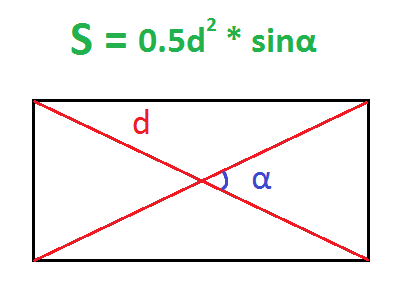
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
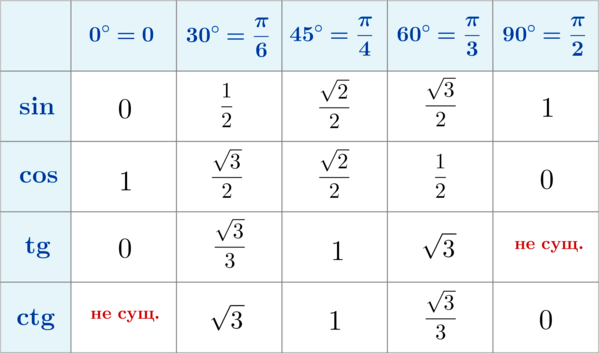
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
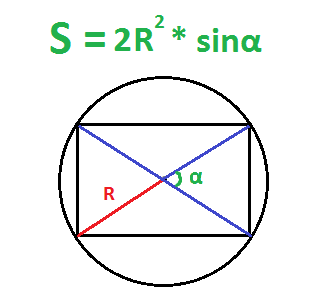
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
( 1 оценка, среднее 5 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
Содержание
- – Как найти площадь прямоугольника если известна высота?
- – Как найти площадь прямоугольника если известны стороны?
- – Как найти площадь прямоугольника если известна площадь?
- – Что нужно сделать чтобы найти площадь?
- – Что такое площадь для 3 класса?
- – Что такое площадь в математике 4 класс?
- – Что значит найти площадь фигуры?
Как найти площадь прямоугольника если известна высота?
Значит для того, чтобы найти площадь прямоугольника нужно его ширину умножить на длину. В виде формулы это можно представить как S = h*b, где S-площадь, h-высота, b-ширина. Или так: площадь прямоугольника = ширина х длину.
Как найти площадь прямоугольника если известны стороны?
Площадь прямоугольника равна произведению его длины на ширину.
Как найти площадь прямоугольника если известна площадь?
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина. Проверить полученный результат поможет онлайн-калькулятор площади прямоугольника.
Что нужно сделать чтобы найти площадь?
Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Что такое площадь для 3 класса?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. … Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Что такое площадь в математике 4 класс?
Площадь-это свойство фигур занимать место на плоскости. … Квадратный миллиметр- единица измерения площади, равная площади квадрата со стороной 1мм. Основная и дополнительная литература по теме урока: Математика: 4 класс: учебник в 2 ч.
Что значит найти площадь фигуры?
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. … В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Интересные материалы:
Сколько кирпича в1м2?
Сколько кирпичей на поддоне?
Сколько кирпичей в кладке в один кирпич?
Сколько кирпичей в одной упаковке?
Сколько кирпичей в поддоне облицовочного?
Сколько комбикорма съедает курица в день?
Сколько кондиционеров нужно в однокомнатную квартиру?
Сколько корма нужно давать кролику в день?
Сколько корма нужно в день для гусей?
Сколько корма съедает биг 6?
Периметр и площадь параллелограмма или прямоугольника рассчитываются по следующим формулам:
- Площадь. S=a* h, где a — длина ширины, h — высота.
- Периметр. P= 2*(a+h ).
Расчет площади:
Для проведения подсчетов необходимо ввести высоту и ширину фигуры.
Важно!
Ввод десятичной дроби также допустим.
Работа калькулятора:
Программа подсчитает периметр и площадь фигуры и выведет их на монитор с точностью до трех знаков после запятой.
Расчет площади параллелограмма или прямоугольника: ширина×высота
| Введите длину ширины и высоты = | |
| Площадь Прямоугольника = |
Периметр параллелограмма или прямоугольника: 2(ширина) + 2(высота)
| Введите длину ширины и высоты = | |
| Периметр Прямоугольника = |
Area of rectangle is the region covered inside the boundaries of the rectangle. A rectangle is a quadrilateral in which opposite sides are equal and parallel. The diagonals of a rectangle are equal and are perpendicular bisectors to each other. All the angles of the rectangles are 90°. A rectangle is similar to a parallelogram. We can say that all the rectangles are parallelograms but its converse is not true.
Table of Contents:
- Definition
- Units
- Formula
- How to Calculate the Area of Rectangle
- Area by Diagonal
- Area by perimeter
- Derivation
- Solved Examples
- FAQS
What is the Area of a Rectangle?
Definition – The area of a Rectangle is the region occupied by a rectangle within its four sides or boundaries.
The area of a rectangle is the space enclosed by the boundaries of the rectangle. In general, the area of any shape is the space enclosed by the geometrical shape. We can also say that the space enclosed by the perimeter of the rectangle is the area of a rectangle. The perimeter of a rectangle is the sum of all the sides. For a rectangle, the area is the multiplication of its length by its breadth. The opposite sides of the rectangle are equal, and if the length and breadth are also equal, then the shape becomes a square. Therefore, every square is a rectangle. The below-given diagram shows the rectangle and its area,

Area of Rectangle
Unit of Area of Rectangle
The area of a rectangle is measured in square units and the standard unit for measuring the area of a rectangle is m2. Other units widely used for measuring the area of the rectangle are cm2, mm2, and others.
|
Side |
Area |
|---|---|
| meter(m) | m2 or (meter)2 |
| centimeter(cm) | cm2 or (centimeter)2 |
Area of a Rectangle Formula
The formula for the area of a rectangle is the multiplication of length (L) and breadth (B).
| The formula of the Area of a Rectangle | |
|---|---|
| Area of Rectangle | A = L x B |
where ,
L is the length of the rectangle
B is the breadth of the rectangleNote:-
If the unit of length and breadth is not exact then it should be transformed into one unit. For e.g. If the length is in cm and breadth in m then both dimensions should be adjusted either to m or cm.
How to Find the Area of a Rectangle?
The area of the rectangle is defined as the product of its length and breadth. Following are the steps that help calculate the area of the rectangle,
Step 1: Note down the dimensions of the rectangle.
Step 2: Calculate the product of the length and breadth of the rectangle.
Step 3: Write the answer in respective square units.
Example: Find the area of a rectangle whose length is 20 inches and breadth is 50 inches.
Solution:
The formula for area of rectangle is given:
Area = L × B
Area = 20 × 50
Area = 1000 inches2
Thus, the required area is 1000 inches2
Area of a Rectangle with Diagonal
The area of the rectangle can be found by two methods which are:
Method 1:
We can find the value of the missing side using the Pythagoras theorem and then find the area. Let us understand this using an example.
The diagonal of the rectangle is the line joining opposite vertices. The diagonal of the rectangle is calculated using Pythagoras’s Theorem

Method 1 to find the Area of the Rectangle
(Diagonal)2 = (Length)2 + (Breadth)2
Length2 = (Diagonals2 – Breadth2)
Length = √(Diagonals2 – Breadth2)
The formula for the area of a rectangle is calculated by:
Area = Length × Breadth
Area = √(Diagonals2 – Breadth2) × Breadth
Area = Breadth √(Diagonals2 – Breadth2)
Method 2:
If both the diagonals of the rectangle are given then its area can be found with the help of the area of the quadrilateral formula.
Let a rectangle ABCD have diagonals as AC and BD and their length is d1 and d2 then its area is given by,
Area of rectangle ABCD = 1/2 × d1 × d2
Example: Find the area of a rectangle whose length of the diagonals is 10 cm and 14 cm.
Solution:
The formula for area of rectangle is,
Area = 1/2 × d1 × d2
Area = 1/2 × 10 × 14
Area = 70 cm2
Thus, the area of required rectangle is 70 cm2.
Area of Rectangle using Perimeter
To calculate the area of a rectangle using the perimeter and one dimension follow the following steps,
Step 1: Note the perimeter and the given dimension.
Step 2: Use the perimeter formula to find the other dimension.
Step 3: Use the area of the rectangle formula and substitute the required value obtained in Step 2
Step 4: Simplify the expression and add unit2 to get the final answer.
The example given below explains the above concept.
Example: Find the area of a rectangle when the perimeter is 28 cm and the breadth is 8 cm.
Solution:
Given,
Perimeter of Rectangle = 28 cm
length = 8 cm
breadth(b) = ?
Using Perimeter of rectangle formula,
Perimeter of rectangle = 2 (l + b)
28 = 2 (8 + b)
14 = 8 + b
b = 6 cm
Thus the breadth of rectangle is 6 cm
Area of Rectangle = l × b
= 8 × 6 = 48 cm2
Thus, the area of the Rectangle is 48 cm2
Derivation of Area of a Rectangle
The area of a rectangle is the product of length and breadth. This can be derived by dividing the rectangle into two triangles. The triangles are equal as the base and height of the two triangles will be equal.
Let’s derive the formula for the area of a rectangle, the image given below shows that a rectangle is made by joining two equal right-angle triangles.

Area of a Rectangle Formula Derivation
- Area of Rectangle = 2 (Area of Triangle)
- Area of Rectangle = 2 (1/2 × Base × Height)
- Area of Rectangle = 2 (1/2 × AB × BC)
- Area of Rectangle = AB × BC
- Area of Rectangle = Length × Breadth.
Thus, the area of the rectangle formula is derived.
Solved Examples on Area of Rectangle
Example 1: The length and width of a rectangle are 6 units and 3 units, respectively. Find the area of the rectangle.
Solution:
Given,
length = 6 unit
breadth = 3 unitsArea of rectangle = length × breath
= 6 × 3
= 18 square unitsThus, the area of given rectangle is 18 square units
Example 2: Find the area of a rectangle whose height is 10 cm and width is 2 cm.
Solution:
Given,
Height = 10 cm
Width = 2 cmArea of Rectangle = width × height
Area of Rectangle = 10 × 2 = 20
Therefore, the area of the rectangle is 20 cm2.
Example 3: A rectangular panel has a width of 150 mm and a height of 99 mm. Find the area of this panel.
Solution:
Given,
Height = 99 mm
= 9.9 cmWidth = 150 mm = 15 cm
Area of Rectangle = width × height
Area of Rectangle = 15 × 9.9
Therefore, the area of the rectangle = 148.5 cm2.
Example 4: The height of a rectangular net is seen to be 20 cm. Its area is seen to be 260 cm2. Find the width of the provided net.
Solution:
Given,
Height = 20 cm
Area = 260 cm2Area of Rectangle = width × height
Therefore,
width = Area / height
width = 260/20
width = 13 cm
Thus, the width of the rectangle is 13 cm
Example 5: The height and width of a rectangular desk are 40 m and 20 m, respectively. If a carpenter charges ₹ 2 per m2 for his work, how much would it cost to make the whole desk?
Solution:
Given,
Height of Desk = 40 m
Width of Desk = 20 mArea of top of Desk = width of desk × height of desk
Area of top of Desk = 40 × 20
Area of top of Desk = 800 m2
At the cost of ₹ 2 per m2,
The cost for making top of the desk is 800 × 2 = ₹ 1600
Example 6: A wall whose length and width are 60 m and 40 m respectively needs to be painted. Find the quantity of the paint required if 1 litre of paint can paint 400 m2 of the wall.
Solution:
Given,
Length of wall = 60 m
Width of wall = 40 m
Area of wall = width × length
Area of wall = 60 × 40
Area of wall = 2400 m2
Paint required for 400 m2 of wall = 1 litre (given)
Paint required for 2400 m2 of wall = 2400 / 400 × 1 = 6 litre.
Thus, the paint required to paint the wall is 6 litre.
Q7: If the length and breadth of the rectangular glass slab are 6 m and 4 m respectively. Then finds its area.
Solution:
Length of the rectangular slab is 6 m
Breadth of the rectangular slab is 4 m
Area of rectangular slab = length × breadth
= 6 × 4
= 24 m2Here, the area is measured in m2.
Related Articles:
- Area of Square
- Area of a Triangle
- Area of Circle
- Area of Quadrilateral
- Area of Rhombus
- Area of Trapezium
- Area of Parallelogram
FAQs on Area of Rectangle
Q1: What is the formula for the area of a rectangle?
Answer:
Area (A) of rectangle formula is the product of the length and breadth. It can be defined as the space occupied by its boundaries.
Q2: What is the unit of area of a rectangle?
Answer:
The unit of the area of rectangle are meter2, centimeter2, inches2, etc. In general, it is unit2.
Q3: What is the perimeter of a rectangle?
Answer:
The perimeter of rectangle is the sum of the length of all its boundaries. The formula for perimeter of rectangle is given as;
P = 2 (Length + Breadth)
Q4: How to find the area of a rectangle?
Answer:
For a rectangle whose length is l and breadth is b then its area can be calculated by using the formula,
Area = l × b
Q5: How to find the area of a rectangle with a diagonal?
Answer:
The area of the rectangle when its diagonal is given is calculated using the formula,
Area = 1/2 × d1 × d2
where
d1 is the first diagonal.
d2 is the second diagonal.
Q6: How to find the area of a rectangle when a perimeter is given?
Answer:
The area of a rectangle when its perimeter and any one side is given can be calculated by,
Step 1: Use the perimeter of the rectangle formula to find the relation between length (l) and breadth (b).
Step 2: One dimension is already given. Use the relation to find the other dimension.
Step 3: When both dimensions are known use the area formula to find the area.
Q7: How to calculate the area of a quadrilateral with 4 different sides?
Answer:
The area of a quadrilateral with all fours sides different and both diagonal given are,
Area = 1/2 × d1 × d2
where
d1 is the first diagonal.
d2 is the second diagonal.
Q8: Is the area of a rectangle equal to the area of a square?
Answer:
No, it is not necessary that the area of the rectangle is equal to the area of square. The condition where both the areas are equal is when the length and breadth in a rectangle are equal.
как найти площади прямоугольника с высотой (формула) ?
Найдите правильный ответ на вопрос ✅ «как найти площади прямоугольника с высотой (формула) ? …» по предмету 📘 Алгебра, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы