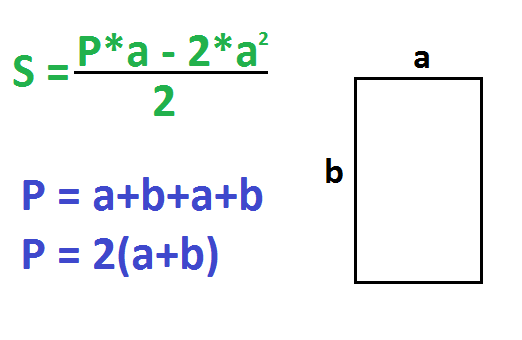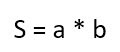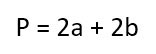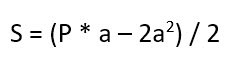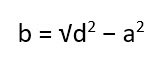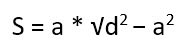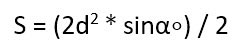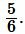Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
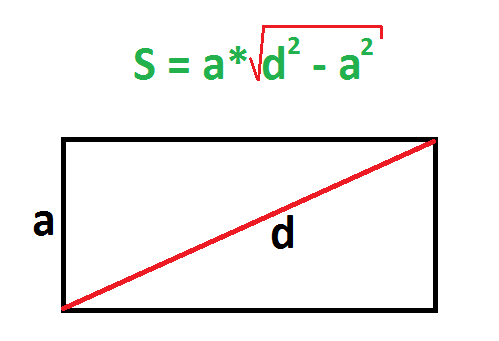
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
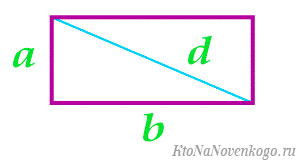
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
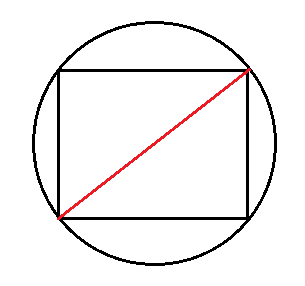
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
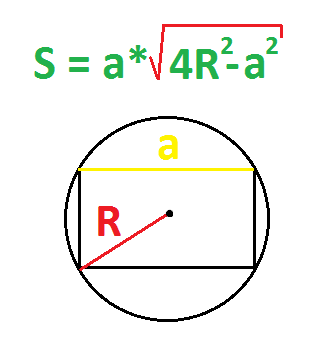
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
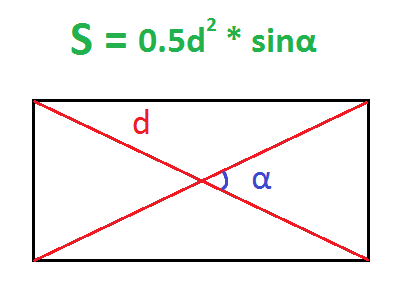
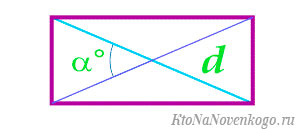
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
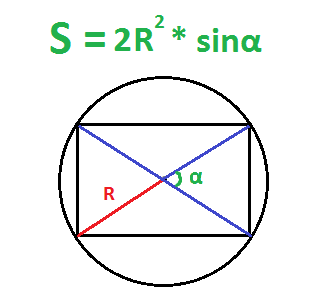
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
11 408
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
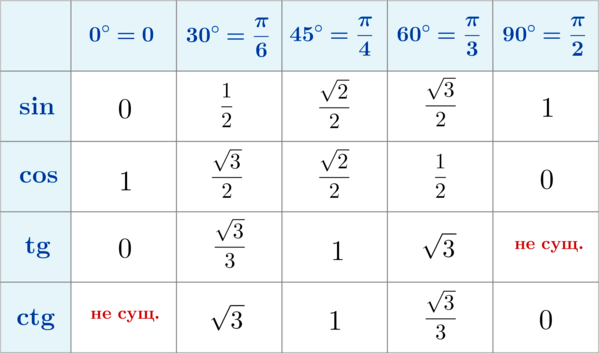
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
( 1 оценка, среднее 5 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
Площадь прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.
Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
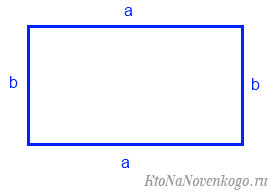
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:
А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».
Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
Возьмем, к примеру, такой прямоугольник:
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
И тогда обратные расчеты выглядят вот так:
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
- Ну и второй вариант – воспользоваться сразу готовой формулой:
Площадь прямоугольника через диагональ
-
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
Второй вариант – опять же сразу прибегнуть к готовой формуле:
-
Если известны длина диагоналей и угол между ними.
В этом случае стоит воспользоваться вот такой формулой:
Вот и все, что нужно знать о вычислении площади прямоугольников.
Площадь прямоугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольника. Для нахождения площади прямоугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Площадь прямоугольника. Определение
Определение 1. Площадь прямоугольника − это величина той части плоскости, которую занимает прямоугольник.
Площадь прямоугольника. Доказательство
Теорема 1. Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон :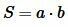
Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S (Рис.1). Докажем, что 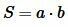
Достроим прямоугольник до квадрата со стороной a+b (Рис.2). Площадь этого квадрата равна (a+b)·(a+b) (см. статью Площадь квадрата онлайн).
С другой стороны, данный квадрат состоит из двух квадратов со сторонами со сторонами a и b и площадями a2 и b2, соответственно и из двух прямоугольников с площадями S. Поэтому сумма площадей этих двух квадратов и двух прямоугольников равна площади квадрата со стороной a+b:
Упрощая полученное равенство, получим: 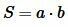
Площадь прямоугольника через стороны
Из вышеизложенной теоремы следует, что площадь прямоугольника через его смежные стороны вычисляется из формулы:
Пример 1. Стороны прямоугольника равны 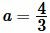
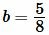
Решение. Для нахождения площади прямоугольника воспользуемся формулой (1). Подставим 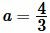
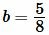
Ответ:
Площадь прямоугольника через сторону и диагональ
Пример 2. Известна сторона прямоугольника 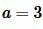
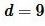
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления площади прямоугольника через диагональ и сторону:
Подставим 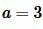
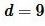
Ответ:
Площадь прямоугольника через периметр и сторону
Пример 3. Известны сторона прямоугольника 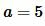
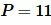
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (4) в (1), получим формулу вычисления площади прямоугольника через периметр и сторону:
Подставим 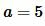
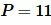
Ответ:
Площадь прямоугольника через диагональ и периметр
Пример 4. Известны диагональ прямоугольника 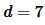
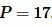
Решение. Найдем сначала стороны прямоугольника. Запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (9), получим квадратное уравнение относительно неизвестной ( a ):
Вычислим дискриминант квадратного уравнения (10):
Подставляя значения 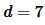
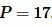
Поскольку дискриминант неотрицательное число, то такой прямоугольник существует.
Стороны прямоугольника вычисляются из формул:
Почему ( small b ), как и ( small a ) получается неотрицательным, посмотрите “примечание” на странице Прямоугольник. Онлайн калькулятор.
Площадь прямоугольника по двум сторонам равна:
Подставляя (12) в (13), получим:
Далее, из (11) и (14) следует:
Подставляя 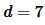
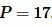
Ответ:
Смотрите также:
- Прямоугольник. Онлайн калькулятор
Naumenko
Высший разум
(856097)
11 лет назад
1. берется полупериметр. те а+в=10 для примера
2. выражается одна сторона через другую а=10-в
3. составляется выражение для площади: в*(10-в) и …
дальше вычислить что – либо затруднительно. тк не хватает информации.
НО! если периметр не очень большое число. то можно подбором найти а и в.. .
наверное. в исходном условии есть еще какие-то слова.
Вовчик
Мыслитель
(6652)
11 лет назад
например периметр 30
один прямоугольник имеет стороны 10 и 5, при этом площадь 50
другой 2 и 13, при этом площадь 26
третий 8 и 7, и площадь при этом 56
вот ведь какая хрень..