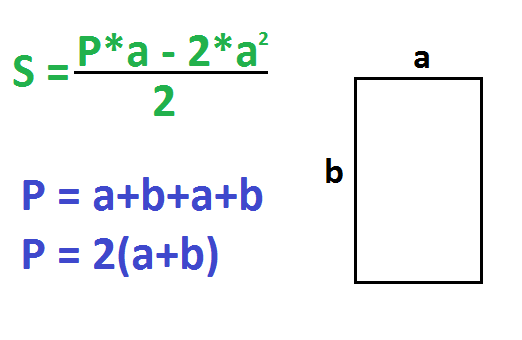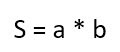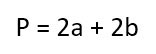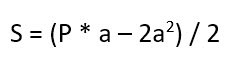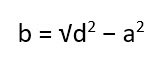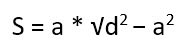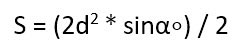Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
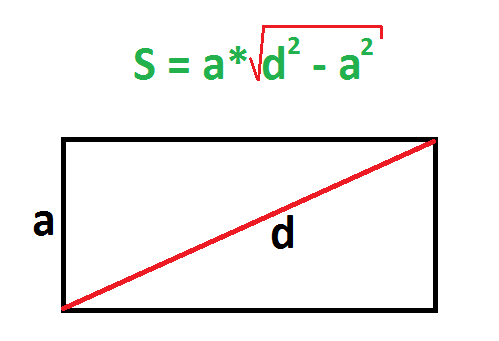
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
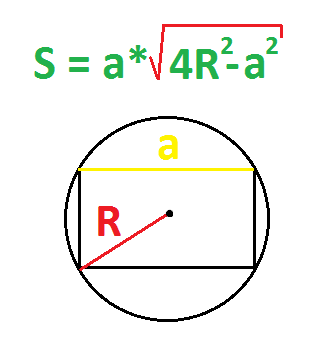
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
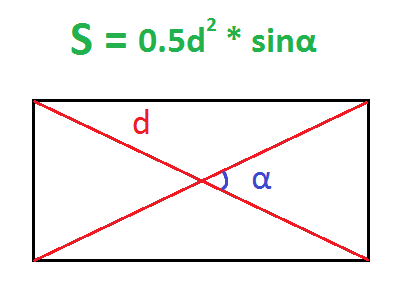
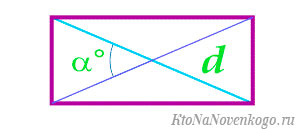
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
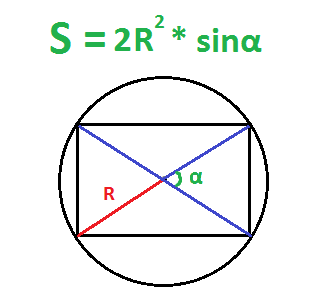
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
11 406
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
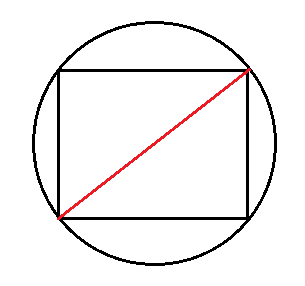
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
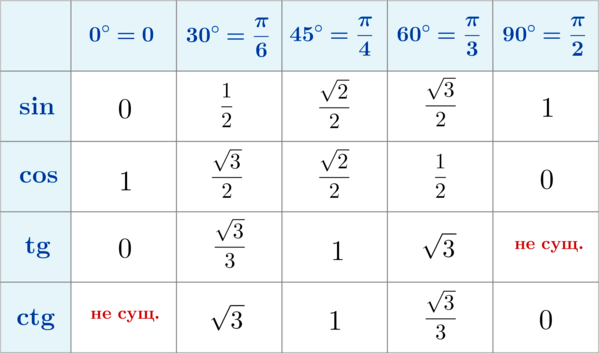
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
( 1 оценка, среднее 5 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
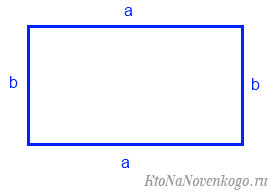
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
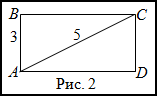
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Сегодня клоун Бим и дрессировщик Бом вместе с ребятами применяют на практике знания, как найти площадь для прямоугольника с разными сторонами.
Площадь фигуры — это размер куска плоскости внутри границ фигуры, измеренный в единицах измерения площади.
Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника (с разными сторонами), если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат укрупняют или раздробляют (см. Статью о переводе из одной единицы измерения площади в другую).
Содержание статьи:
Площадь — это?
Площадь любого куска плоскости (фигуры)— это размер этого куска плоскости (куска плоскости внутри границ фигуры), измеренный в единицах измерения площади.
Бим и Бом пришли на работу в цирк пораньше. Бим зашел к Бому в гримерку.
— Привет, Бим!
— Привет, Бом!
— У нашей Буфетчицы сегодня день рождения. Я купил очень вкусных конфет, только вот упаковка видишь какая длинная. У тебя есть какая-нибудь красивая коробка, куда мы можем сложить конфеты и подарить Буфетчице?
— У меня много разных красивых коробочек. Но как мы узнаем, какая из них подходит, чтобы вместились все конфеты и было красиво?
Бом и Бим задумались.
— Ура!!! Придумал, — нашелся Бим. — У каждой коробки есть плоское донышко. Давай вычислим площади донышек у каждой коробки, то есть измерим площадь донышек в единицах измерения площади — квадратных сантиметрах.
— Тогда найдем, какая коробка подходит больше всего, — подхватил Бом. — Начнем с упаковки, где лежат конфеты. У упаковки донышко в виде прямоугольника. Значит, достаточно измерить длины короткой и длинной стороны.
— А чем будем измерять? — задумался Бим.
— Сейчас поищу, — ответил Бом. — Вот у меня есть сантиметр, линейка и листочек в клеточку.
— Дай, пожалуйста, мне листочек в клеточку, — попросил Бом. — Я проверю, что донышко упаковки — прямоугольник.
Как найти площадь прямоугольника с разными сторонами. Площадь прямоугольника — это?
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника, если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат можно укрупнить или раздробить (см. Статью о переводе из одной единицы измерения площади в другую).
Бим приложил листочек к углам донышка упаковки.
— Проверил: у упаковки четыре угла, и все они — прямые. Тогда донышко упаковки — прямоугольник.
Бом начал читать свои записи:
“Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника. Как найти площадь прямоугольника (с разными сторонами), если известны длины его сторон? Достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади”.
— Теперь надо измерить длины двух сторон. Упаковка — длинная, тогда лучше взять сантиметр.
Бим измерил упаковку.
— Короткая сторона 8 см, длинная — 72 см. Вспоминаем, что для вычисления площади прямоугольника надо длину одной стороны умножить на длину прилежащей стороны. Умножаем:
72 х 8 =576 кв.см (см2).
— Сейчас принесу из подсобки коробки, которые у меня есть, — побежал Бом.
И — надо же! — по дороге Бом встретил Олю, Колю и Васю, которые пришли пораньше на представление.
— Ребята, как хорошо, что вы здесь! Идемте, поможете нам с Бимом подобрать Буфетчице на день рождения коробку.
Бом достал из подсобки коробки, и они все вместе вернулись к Биму.
— Ребята, мы с Бимом измерили площадь упаковки конфет, которые мы хотим переложить в более красивую коробку. Красиво сложим и подарим Буфетчице на день рождения, — объяснил Бим.
— Давайте вычислим площадь донышка каждой коробки, — предложил Вася. — В коробку, у которой площадь донышка равна площади донышка упаковки, мы переложим конфеты.
— Как здорово, что Бом принес все коробки, донышки у которых имеют вид прямоугольника! — обрадовался Коля. — Как найти площадь прямоугольника с разными сторонами? Надо измерить длины двух прилежащих сторон в одинаковых единицах измерения длины и их перемножить, — получим площадь прямоугольника в единицах измерения площади. Для коробок удобнее всего измерять длины сторон в сантиметрах, а площадь самих прямоугольников уже будет в квадратных сантиметрах. Оля, давай проверим, что донышки коробок — прямоугольники.
Коля и Оля взяли листочек в клеточку и с помощью него проверили, что у донышек все углы прямые.
Затем Коля, Вася и Оля вооружились листочком в клеточку, линейкой и сантиметровой лентой и измерили в сантиметрах длины прилежащих сторон донышек коробок.
Первым управился Коля:
— У меня большая сторона 36 сантиметров и короткая 16 сантиметров. Получаем площадь моей коробки
36 х 16 = 576 (кв.см).
Следующим был Вася:
— У меня длина коробки 30 см, а ширина — 20 см. Для вычисления площади коробки надо длину умножить на ширину прямоугольника. Получаем:
30 х 20 = 600 (кв.см)
Оля измеряла тщательнее всех, ведь у нее коробка была похожа на квадрат. Но надо было убедиться, точно ли у этой коробки равны обе стороны. Так и оказалось:
— У меня прилежащие стороны одинаковые по длине, обе равны 24 см. Перемножаем длины двух прилежащих сторон, получаем: 24 х 24 = 576 (кв.см).
— Тогда у нас выходят 3 коробки с одинаковыми площадями донышек — у упаковки, — подытожил Бом:
8 х 72 = 576 (кв.см), —
и еще у двух коробок
16 х 36 = 576 (кв.см),
24 х 24 = 576 (кв.см),
а также одна коробка площадью больше, чем у упаковки
30 х 20 = 600 (кв.см).
— Какую же коробку выбрать? — озадаченно спросил Бим.
— Давай возьмем в виде квадрата, посмотрите какая здесь красивая крышка! — решил Бом.
Ребята выложили конфеты из упаковки в коробку.
— Ага, — посмотрел Бом. — получились три ряда. Какая же площадь донышка одного ряда? Длина ряда 24 см, ширина — 8 см. Значит площадь донышка одного ряда равна:
24 х 8 = 192 (кв.см).
Всего три одинаковых ряда
192 х 3 = 576 (кв.см).
Ура! Все совпадает!
Бим, все же, спросил:
— Сейчас мы измеряли площадь в квадратных сантиметрах. А какие еще есть единицы измерения площади?
Единицы измерения площади
Единицы измерения площади — это площадь квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м). (См. статью “Единицы измерения площади”)
В каких единицах измерения площади мы можем записать площадь донышка одного ряда? — продолжил вопрос Бим.
Оля ответила сразу:
— Если мы будем укрупнять, то в дециметрах и сантиметрах.
576 кв.см = 5 кв.дм 76 кв.см
— А если мы будем раздроблять — в миллиметрах, — добавил Коля. —
576 кв.см =576 х 100 (кв.мм).
А еще единицы измерения площади 1 кв.м (квадрат со стороною 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
— Теперь я подпишу открытку. У меня красивый артистический почерк, — вызвался Бом.
— Хорошо, Бом. А мы с ребятами составим вопросы и ответы на них, — согласился Бим.
— Первый вопрос: Что называется площадью? — начал Вася.
— Второй вопрос: Дайте определение прямоугольника. — продолжил Коля. —
И третий вопрос: Что такое площадь прямоугольника?
— Четвертый вопрос: Как найти площадь прямоугольника (с разными сторонами)? — закончила Оля.
— И еще один, пятый, вопрос: Какие вы знаете единицы измерения площади? — добавил Бим.
Теперь я запишу ответы для проверки, — продолжил клоун:
1. Площадь — это размер куска плоскости внутри фигуры.
2. Прямоугольник — это фигура с 4-мя прямыми углами и с замкнутой границей из четырех отрезков.
3. Площадь прямоугольника — это площадь куска плоскости внутри границ прямоугольника.
4. Как найти площадь прямоугольника? Для нахождения площади прямоугольника перемножаются длины двух прилежащих сторон. Результат записывается в единицах измерения площади.
5. Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Итог подвел Бом:
— Мы сегодня узнали :
- что такое площадь
- что такое площадь прямоугольника
- как найти площадь прямоугольника
- единицы измерения площади.
Всем спасибо за помощь.
Заключение
Итак, теперь мы знаем ответ на вопрос: Как найти площадь прямоугольника с разными сторонами. А вам приходилось дарить конфеты в коробочках? Как видим, можно, в случае чего, упаковать подарок более изящно, а заодно — и математику повторить.
Идея необычной подачи материала принадлежит замечательному преподавателю математики Стуловой Лилии Валериевне.
Ждём Ваши оценки и комментарии!)))
Площадь прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.
Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:
А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».
Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
Возьмем, к примеру, такой прямоугольник:
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
И тогда обратные расчеты выглядят вот так:
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
- Ну и второй вариант – воспользоваться сразу готовой формулой:
Площадь прямоугольника через диагональ
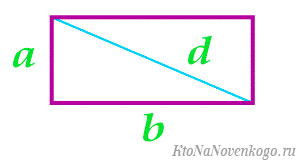
-
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
Второй вариант – опять же сразу прибегнуть к готовой формуле:
-
Если известны длина диагоналей и угол между ними.
В этом случае стоит воспользоваться вот такой формулой:
Вот и все, что нужно знать о вычислении площади прямоугольников.