Рассчитать площадь прямоугольника с подробным решением. Калькулятор находит площадь по формуле через длину и ширину прямоугольника. Основные способы и объяснение формул, по которым вы сможете самостоятельно решить свои задачи.
Онлайн-калькулятор площади прямоугольника
Вначале давайте разберемся с определением. У прямоугольника есть 4 стороны. Каждая сторона равна противоположной и параллельна ей. Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.
Все 4 угла, находящиеся внутри прямоугольника, — прямые. То есть каждый угол равен 90°.
Формула площади прямоугольника через его стороны
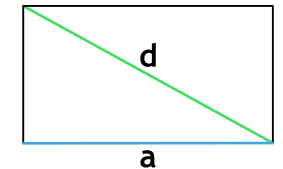
Чтобы найти площадь SS прямоугольника, нужно перемножить две его стороны: сторону aa умножаем на сторону bb.
S=a⋅b.S = a cdot b.
У нас есть прямоугольник ABCDABCD. Одна его сторона ABAB равна 55 см, вторая BCBC равна 33 см. Нам нужно найти его площадь SS.
Решение:
Чтобы найти площадь SS, нужно умножить сторону ABAB на сторону BCBC и получаем: S=5⋅3S = 5 cdot 3.
Ответ: S=15S = 15 см2.
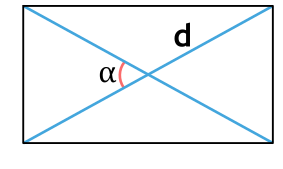
Формула площади прямоугольника через диагонали
Площадь прямоугольника можно также рассчитать, зная длину диагоналей и острый угол между ними:
S=12d2sinα.S = frac {1}{2}d^2 sin alpha.
Помним, длины диагоналей в прямоугольнике равны и при пересечении делятся пополам.
Дан прямоугольник ABCDABCD. Его диагональ ACAC равна 88 см, а острый угол между диагоналями 30°30°. Найдите площадь фигуры.
Используем приведенную выше формулу и получаем:
S=12⋅82⋅sin30∘=12⋅64⋅12=644=16S = frac{1}{2} cdot 8^2 cdot sin 30^{circ} = frac{1}{2} cdot 64 cdot frac{1}{2} = frac{64}{4} = 16
Ответ: S=16S = 16 см2.
Не знаете, как решить задачу по геометрии онлайн? Оформите заказ на Студворк!
Тест по теме «Площадь прямоугольника»
Площадь прямоугольника через диагональ
В прямоугольнике диагонали равны между собой. Если известен угол α между диагоналями (длина диагоналей равна d), то площадь прямоугольника можно найти по формуле:
Sпр = 0,5 * d² * sinα.
Например, если угол между диагоналями равен 30°, а диагонали равны 5 см, то площадь будет равна:
Sпр = 0,5 * 25 * 0,5 = 6,25 см.
Если неизвестен угол между диагоналями, то будет нужно найти стороны прямоугольника. А затем воспользоваться формулой:
Sпр = a * b.
Как известно, диагональ прямоугольника делит его на 2 равных прямоугольных треугольника. Поэтому задача сводится к тому, чтобы найти катеты прямоугольного треугольника через гипотенузу.
Кроме длины диагонали требуется знать либо одну из сторон прямоугольника, либо отношение сторон, либо угол между стороной и диагональю.
1) Если известна диагональ (пусть она будет равна d) и одна из сторон (например, b), то выражаем неизвестную сторону из формулы:
a² + b² = c² -> a = √(c² – b²).
Sпр = a * b = √(c² – b²) * b.
Например, если диагональ d = 5 см и сторона b = 3 см, то a = √(25 – 9) = √16 = 4 см.
Площадь прямоугольника равна 3 * 4 = 12 см.
2) Если известно отношение сторон, то задача сводится к нахождению обеих сторон через составление уравнения.
Например, если стороны относятся как 2:3, а диагональ равна 13 см, то можно составить уравнение:
(2x)² + (3x)² = 4x² + 9x² = 169.
13x² = 169.
x = √13.
Значит, a = 2√13 см и b = 3√13 см.
Площадь прямоугольника равна 2√13 * 3√13 = 6 * 13 = 78 см.
3) Если известна диагональ и один из прилежащих к диагонали углов, то нужно воспользоваться формулами:
a = d * cosβ (β – прилежащий угол) и b = d * sinα (α – противолежащий угол).
Например, d = 10 см и угол α = 30°.
a = 10 * cos30° = 10√3 / 3.
b = 10 * sin30° = 5 см.
Площадь прямоугольника равна 5 * (10√3 / 3) ≈ 28,33 см.
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
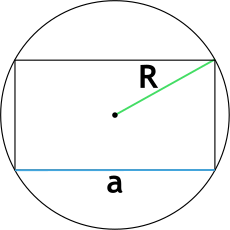
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
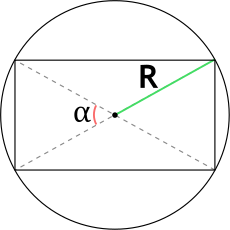
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым

{S = a cdot b}
Найти площадь прямоугольника
Найти площадь прямоугольника вы сможете с помощью калькуляторов или по формулам вручную. Для этого мы подготовили 6 формул и калькулятор, который позволяет произвести расчет по любой из них.
Прямоугольник — четырехугольник, у которого все углы равны 90° (прямые).
Содержание:
- калькулятор площади прямоугольника
- формула площади прямоугольника через стороны
- формула площади прямоугольника через сторону и диагональ
- формула площади прямоугольника через диагонали и угол
- формула площади прямоугольника через сторону и периметр
- формула площади прямоугольника через сторону и радиус описанной окружности
- формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
- примеры задач
Формула площади прямоугольника через стороны
S = a cdot b
a, b – стороны прямоугольника (длина и ширина)
Формула площади прямоугольника через сторону и диагональ
S=a cdot sqrt{d^2 – a^2}
d – диагональ прямоугольника
a – сторона прямоугольника
Формула площади прямоугольника через диагонали и угол
S = dfrac{1}{2} cdot d^2 cdot sin(alpha)
d – диагональ прямоугольника
α – угол между диагоналями
Формула площади прямоугольника через сторону и периметр
S = dfrac{a cdot P – 2a^2}{2}
a – сторона прямоугольника
P – периметр прямоугольника
Формула площади прямоугольника через сторону и радиус описанной окружности
S = a cdot sqrt{4R^2 – a^2}
R – радиус описанной окружности
a – сторона прямоугольника
Формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
S = 2R^2 cdot sin{alpha}
R – радиус описанной окружности
α – угол между диагоналями
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь прямоугольника диагональ которого равна 10 см, а угол между диагоналями равен 30°.
Решение
Так как в условии нам даны диагональ и угол, нам подойдет третья формула.
S = dfrac{1}{2} cdot d^{: 2} cdot sin(alpha) = dfrac{1}{2} cdot 10^2 cdot sin(30°) = dfrac{1}{2} cdot 100 cdot sin(30°) = 50 cdot dfrac{1}{2} = 25 : см^2
Ответ: 25 см²
Для проверки результата воспользуемся калькулятором .
Задача 2
Найдите площадь прямоугольника со сторонами 4 см и 13 см.
Решение
Используем первую формулу.
S = a cdot b = 4 cdot 13 = 52 : см^2
Ответ: 52 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольника если его длина 2 дм а ширина 4 см.
Решение
Задача аналогична предыдущей. Тоже воспользуемся первой формулой. Учтем, что 2 дм = 20 см.
S = a cdot b = 20 cdot 4 = 80 : см^2
Ответ: 80 см²
Проверим ответ на калькуляторе .
Задача 4
Найдите площадь прямоугольника, если его длина равна 7 см а ширина 4 см.
Решение
И снова однотипная задача. Решим ее как и две решенные выше.
S = a cdot b = 7 cdot 4 = 28 : см^2
Ответ: 28 см²
Проверка .
Формула площади прямоугольника через диагональ

4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
Все с начальной школы знают формулу площади прямоугольника. Площадь прямоугольника равняется произведению длины на ширину. Но иногда бывает, что узнать длину или ширину не представляется возможным, зато есть значения диагоналей.
Определения
Поговорим о нескольких определениях, которые необходимы для того, чтобы разобраться в этой теме.
Прямоугольник – это выпуклый четырехугольник, стороны которого попарно равны и параллельны, а углы равняются 90 градусам. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны между собой.
Что такое диагональ? Диагональ – это отрезок, который соединяет противолежащие стороны фигуры. Диагональ существует во всех фигурах, число вершин которых больше 3.
У треугольника диагоналей нет, а у тетраэдра или додекаэдра есть.
Четырехугольники подразделяются на выпуклые и невыпуклые. Выпуклые четырех угольники определяют по следующему правилу: через любые две соседние вершины фигуры проводят прямую. Если фигура лежит по одну сторону от прямой, то четырехугольник выпуклый, если нет – невыпуклый. Все известные четырехугольники являются выпуклыми.
Формула площади прямоугольника
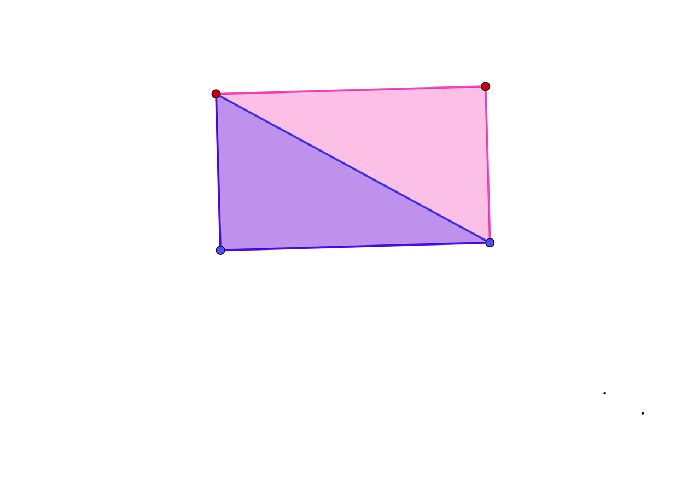
Площадь прямоугольника обычно определяют как произведение длины на ширину. Эта формула выводится через разделение фигуры диагональю на два прямоугольных треугольника. Площадь каждой из фигур это половина произведения катетов. Общая площадь двух фигур целое произведение катетов. Этими катетами как раз и являются длина и ширина прямоугольника.
Но случаются ситуации, когда приходится искать площадь, но значений длины или ширины нет. Что делать тогда? Воспользоваться общей для всех четырех угольников формулой и найти площадь прямоугольника через диагонали.
Площадь любого выпуклого четырех угольника равняется произведению диагоналей на синус угла между ними. Диагонали прямоугольного треугольника равны между собой, поэтому значения угла и одной диагонали хватит для нахождения площади.
$$S={1over2}*d^2*sin(a)$$
Внимательно следите за тем, какой именно угол дан в условиях задачи. Необходим острый угол при диагоналях. Если тупой, то можно воспользоваться формулой смежного угла. Если дан какой-либо из углов между стороной и диагональю, то придется искать другие пути решения.
Возможны ситуации, когда нужно найти площадь, а известен угол между диагональю и стороной и значение диагонали и стороны. Тогда нужно найти площадь прямоугольного треугольника через формулу с применением синуса и удвоить ее.
В этом случае площадь прямоугольника будет равна:
S=d*b*sin(a)
Что мы узнали?
Мы поговорили о площади прямоугольного треугольника. Выделили отдельно формулу площади прямоугольника через диагонали. Поговорили о случаях, когда применение этой формулы невозможно или затруднено и привели альтернативный вариант решения.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
А какая ваша оценка?