Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
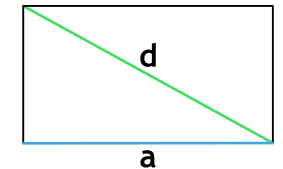
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
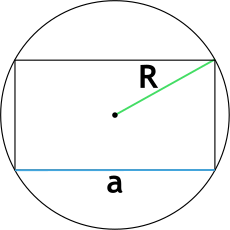
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
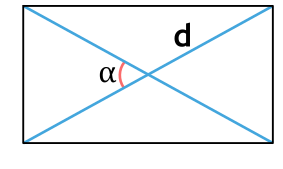
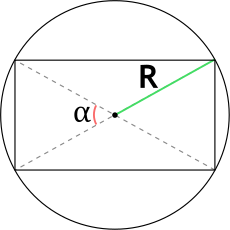
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
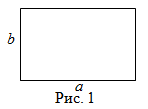
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
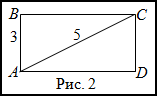
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Площадь прямоугольника

4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении.
Опыт работы учителем математики – более 33 лет.
Понятия площади
Любая фигура имеет свою площадь, а вычисление площади отталкиваются от единичного квадрата, то есть от квадрата с длиной стороны в 1 мм, либо 1 см, 1 дм и так далее. Площадь такой фигуры равна $1*1 = 1мм^2$, либо $1см^2$ и т. д. Площадь, как правило, обозначается буквой S.
Площадь показывает размер части плоскости, которую занимает фигура, очерченная отрезками.
Прямоугольником называется четырехугольник, у которого все углы одинаковой градусной меры и равны по 90 градусов, а противоположные стороны попарно параллельны и равны.
Особое внимание нужно обращать на единицы измерения длины и ширины. Они должны совпадать. Если единицы не совпадают, их переводят. Как правило переводят большую единицу в меньшую, например, если длина дается в дм, а ширина в см, то дм переводят в см, а результат получится в $см^2$.
Формула площади прямоугольника
Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.
Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см2. Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина. Таким образом, можно вывести формулу площади прямоугольника:
S = a · b, где a,b – ширина и длина фигуры.
К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.
Расчет площади прямоугольника, с использованием его диагонали
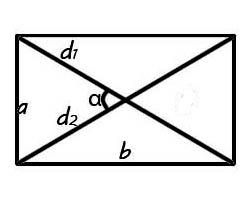
Для того, чтобы рассчитать площадь прямоугольника через диагональ необходимо применить формулу:
$$S = {1over{2}} ⋅ d^2 ⋅ sin{α}$$
Если в задании дано значения угла между диагоналями, а также значение самой диагонали, то можно вычислить площадь прямоугольника по общей формуле произвольных выпуклых четырехугольников.
Диагональ – это отрезок, который соединяет противоположные точки фигуры. Диагонали прямоугольника равны, и точкой пересечения делятся пополам.
Примеры
Для закрепления темы рассмотрим примеры заданий:
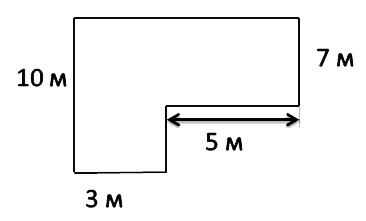
№1. Найти площадь огородного участка, такой формы как на рисунку.
Решение:
Для того чтобы вычесть площадь, необходимо фигуру разбить на два прямоугольника. Один из них будет иметь размеры 10 м и 3 м, другой 5 м. и 7 м. Отдельно находим их площади:
$S_1 =3*10=30 м^2$;
$S_2=5*7=35 м^2$.
Далее необходимо найти их сумму:
$30+35=65 м^2$
Это и будет площадь огородного участка $S = 65 м^2$.
№2. Вычислить площадь прямоугольника, если его диагональ d=6 см. а угол между диагоналями α =300.
Решение:
Значение $sin 30 ={1over{2}} $,
$ S ={1over{2}}⋅ d^2 ⋅ sinα$
$S ={1over{2}} * 6^2 * {1over{2}} =9 см^2$
Таким образом, $S=9 см^2$.
Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Dima Erlichenkov
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
А какая ваша оценка?

{S = a cdot b}
Найти площадь прямоугольника
Найти площадь прямоугольника вы сможете с помощью калькуляторов или по формулам вручную. Для этого мы подготовили 6 формул и калькулятор, который позволяет произвести расчет по любой из них.
Прямоугольник — четырехугольник, у которого все углы равны 90° (прямые).
Содержание:
- калькулятор площади прямоугольника
- формула площади прямоугольника через стороны
- формула площади прямоугольника через сторону и диагональ
- формула площади прямоугольника через диагонали и угол
- формула площади прямоугольника через сторону и периметр
- формула площади прямоугольника через сторону и радиус описанной окружности
- формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
- примеры задач
Формула площади прямоугольника через стороны
S = a cdot b
a, b – стороны прямоугольника (длина и ширина)
Формула площади прямоугольника через сторону и диагональ
S=a cdot sqrt{d^2 – a^2}
d – диагональ прямоугольника
a – сторона прямоугольника
Формула площади прямоугольника через диагонали и угол
S = dfrac{1}{2} cdot d^2 cdot sin(alpha)
d – диагональ прямоугольника
α – угол между диагоналями
Формула площади прямоугольника через сторону и периметр
S = dfrac{a cdot P – 2a^2}{2}
a – сторона прямоугольника
P – периметр прямоугольника
Формула площади прямоугольника через сторону и радиус описанной окружности
S = a cdot sqrt{4R^2 – a^2}
R – радиус описанной окружности
a – сторона прямоугольника
Формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
S = 2R^2 cdot sin{alpha}
R – радиус описанной окружности
α – угол между диагоналями
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь прямоугольника диагональ которого равна 10 см, а угол между диагоналями равен 30°.
Решение
Так как в условии нам даны диагональ и угол, нам подойдет третья формула.
S = dfrac{1}{2} cdot d^{: 2} cdot sin(alpha) = dfrac{1}{2} cdot 10^2 cdot sin(30°) = dfrac{1}{2} cdot 100 cdot sin(30°) = 50 cdot dfrac{1}{2} = 25 : см^2
Ответ: 25 см²
Для проверки результата воспользуемся калькулятором .
Задача 2
Найдите площадь прямоугольника со сторонами 4 см и 13 см.
Решение
Используем первую формулу.
S = a cdot b = 4 cdot 13 = 52 : см^2
Ответ: 52 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольника если его длина 2 дм а ширина 4 см.
Решение
Задача аналогична предыдущей. Тоже воспользуемся первой формулой. Учтем, что 2 дм = 20 см.
S = a cdot b = 20 cdot 4 = 80 : см^2
Ответ: 80 см²
Проверим ответ на калькуляторе .
Задача 4
Найдите площадь прямоугольника, если его длина равна 7 см а ширина 4 см.
Решение
И снова однотипная задача. Решим ее как и две решенные выше.
S = a cdot b = 7 cdot 4 = 28 : см^2
Ответ: 28 см²
Проверка .