Формулы площади поверхности геометрических фигур
Площадь геометрической фигуры
– численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Площадь куба
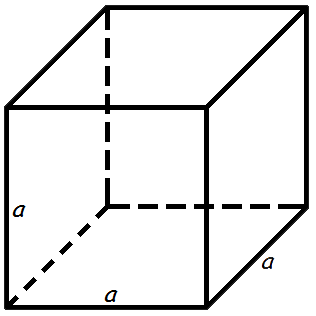
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба:
S = 6 a2
где S – площадь куба,
a – длина грани куба.
Площадь прямоугольного параллелепипеда
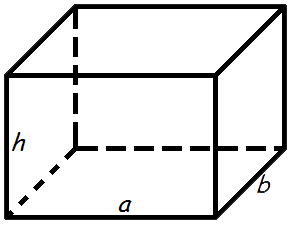
Формула площади поверхности прямоугольного параллелепипеда:
S = 2(a · b + a · h + b · h)
где S – площадь прямоугольного параллелепипеда,
a – длина,
b – ширина,
h – высота.
Площадь цилиндра

Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра:
S = 2 π R h
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра:
S = 2 π R h + 2 π R 2 = 2 π R(R + h)
где S – площадь,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592.
Площадь конуса

Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π.
Формула площади боковой поверхности конуса:
S = π R l
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
S = π R2 + π R l = π R (R + l)
где S – площадь,
R – радиус основания конуса,
l – образующая конуса,
π = 3.141592.
Площадь шара
Формулы площади шара:

-
Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π.
S = 4 π R2
-
Площадь поверхности шара равна квадрату его диаметра умноженного на число π.
S = π D2
где S – площадь шара,
R – радиус шара,
D – диаметр шара,
π = 3.141592.
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
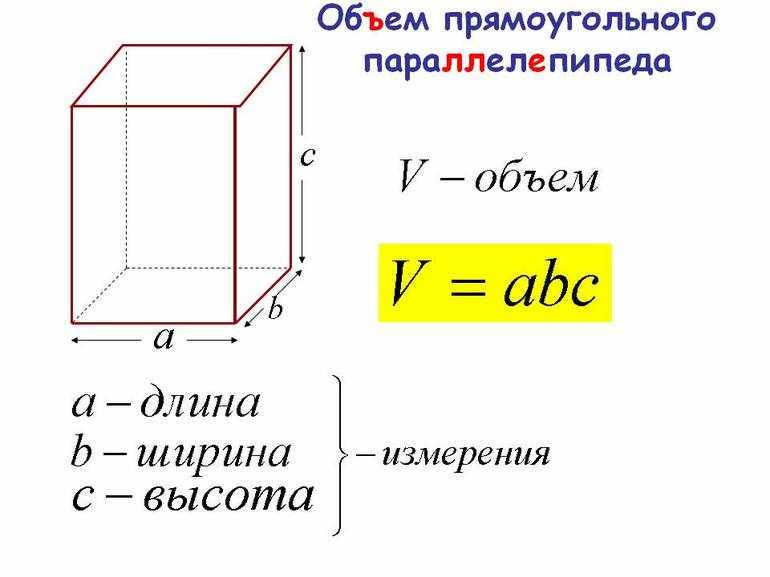
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
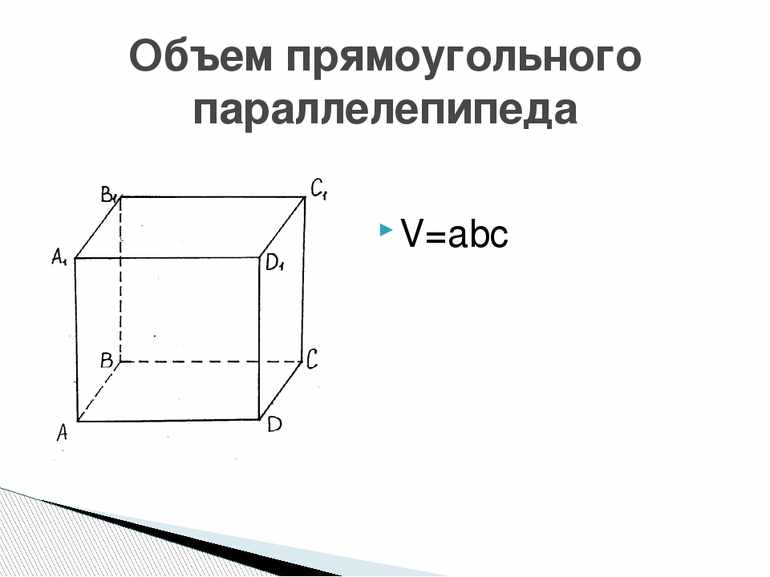
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:

- площадь — двумерная характеристика, определяющая размер фигуры,
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.
Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
- Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
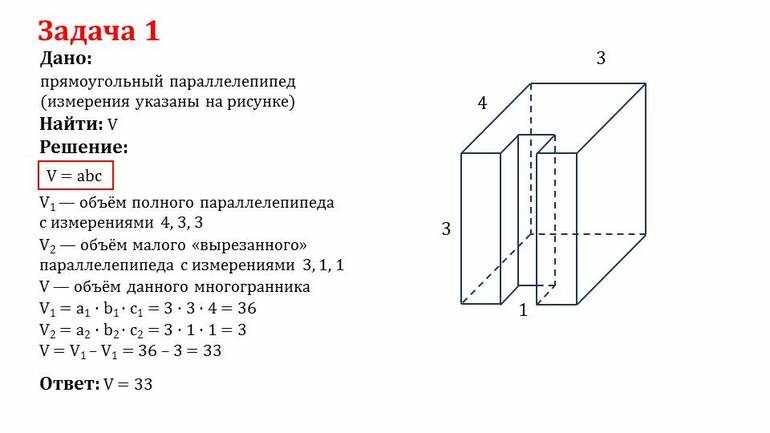
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
- В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 1794

Условие
Как найти:
а) площадь прямоугольника;
б) площадь квадрата;
в) объём прямоугольного параллелепипеда;
г) объём куба?
Запишите эти правила в виде формул.
Решение 1

Решение 2

Решение 3

Популярные решебники
При изучении школьной математики часто встречаются задания, в которых требуется определить полную или боковую площадь поверхности прямоугольного или обычного параллелепипеда. Научимся это делать.
Для того, чтобы научиться вычислять площадь поверхности параллелепипеда необходимо представлять, что это такое.
Содержание:
- Общие понятия
- Нахождение площадей фигур
- Площадь поверхности параллелепипеда
- Площадь поверхности куба
- Площадь поверхности прямоугольного параллелепипеда
- Поверхность параллелепипеда
- Заключение
- Видео
Общие понятия
Изучим основные понятия. В дальнейших наших рассуждениях площадь будем обозначать латинской буквой S, угол между сторонами a и b будем обозначать как (ab).
Параллелепипедом в математике именуется четырехугольная призма, у которой все грани являются параллелограммами.
- Грань — одна из поверхностей пространственного тела.
- Параллелограмм — четырёхугольник с попарно параллельными противоположными сторонами.
- Поверхности параллелепипеда это сумма поверхностей всех его граней.
- Прямоугольный параллелепипед — пространственное тело у которого гранями являются прямоугольники.
- Прямоугольник — четырёхугольник у которого все углы прямые.
- Куб — пространственное тело у которого гранями являются квадраты.
- Квадрат — прямоугольник у которого все стороны равны между собой.
- Равными называются фигуры, совмещающиеся при наложении.

Нахождение площадей фигур
Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.
- Площадь квадрата равна произведению его стороны самой на себя. Формула площади квадрата имеет вид S = a*a = a^2.
- Прямоугольника – вычисляется с помощью умножения большей его стороны (длины) на меньшую его сторону (ширину). Формула площади прямоугольника имеет вид S = a*b.
- Параллелограмма – найти сложнее и имеется несколько различных способов. Наиболее часто в математике применяются формулы для нахождения с помощью стороны и опущенной на неё высоты или двух сторон и синуса угла между ними. Записываются они следующим образом: S = a*h, S = a*b*sin (ab).
Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур.
1. Длина стороны квадрата равна 1600 метров. Определим его площадь.
- S = a*a, отсюда в искомом случае S = 1600*1600 = 2 560 000 метров квадратных.
2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.
- S = a*b, следовательно в нашем варианте получится S = 90*200 = 18 000 метров квадратных.
3. С параллелограммом рассмотрим два случая нахождения.
Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:
- S = a*h = 300*250 = 75 000 метров квадратных.
Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:
- S = a*b*sin (ab) = 550*200*sin 30 = 110 000*0.5 = 55 000 квадратных метров.
Как видно из примеров, приведённых выше, никаких сложностей нет.

Площадь поверхности параллелепипеда
Так как наши тела имеют три принципиально различных варианта, то каждый из них мы рассмотрим в отдельности. Учтём, что полной поверхностью является сумма площадей всех граней тела, а боковой — только боковых граней.
Площадь поверхности куба
Здесь все крайне просто — грани этой фигуры равны между собой, так что S = a*a*6.
На примере это выглядит следующим образом:
Сторона равна 88 сантиметров. Площадь полной поверхности?
При данных условиях имеем:
S = a*a*6 = 88*88*6 = 46 464 сантиметра квадратного.
Площадь поверхности прямоугольного параллелепипеда
Здесь все так же довольно легко — нужно помнить, что противоположные грани равны. Таким образом, находим поверхность трёх различных граней, и каждую удваиваем. Формулы нахождения будут выглядеть следующим образом:
S = 2*(S1 + S2 + S3), где S1, S2, S3 площади всех граней соответственно.
Второй вариант S = 2*(a*b + a*c + b*c), где a, b, c соответствующие рёбра прямоугольного параллелепипеда.
Снова рассмотрим пример. Пусть рёбра прямоугольного параллелепипеда равняются 20, 30 и 40 метров. Площадь полной поверхности?
Имеем, S = 2*(a*b + a*c + b*c) = 2*(20*30 + 20*40 + 30*40) = 2*(600 + 800 + 1200) = 2*2600 = 5 200 квадратных метров.
Как видно, находить площадь прямоугольного параллелепипеда также совершенно несложно.
Поверхность параллелепипеда
Теперь рассмотрим случай когда заданное нам тело имеет вид простого параллелепипеда, его гранями являются обычные параллелограммы. Здесь, как и в предыдущем случае противоположные грани равны. Следовательно, определив поверхность трёх различных граней, мы сможем определить и полную поверхность. Значит, одна из формул опять-таки будет иметь вид:
- S = 2*(S1 + S2 + S3), где S1, S2, S3 площади трёх различных граней соответственно. Запишем исходя из наших рассуждений, ещё две формулы:
- S = 2*(a*h1 + b*h2 + c*h3), где a, b, c соответствующие рёбра параллелепипеда, а h1, h2, h3 опущенные на них высоты.
- S = 2*(a*b*sin (ab) + a*c*sin (ac) + b*c*sin (bc)), где a, b, c соответствующие рёбра, а (ab), (ac), (bc) углы между ними.
Снова приведём пример:
- a = 15, b = 25, c = 25, h1 = 10, h2 = 20, h3 = 15. Пл. полной поверхности? Согласно формуле получим:
- S = 2*(a*h1 + b*h2 + c*h3) = 2*(15*10 + 25*20 + 25*15) = 2*(150 + 500 + 375) = 2*1025 = 2 050 миллиметров квадратных.
В некоторых заданиях требуется определение только площади боковой поверхности параллелепипеда. В таком случае чётко указывается, что является основанием и находится только суммарная пл. четырёх боковых граней. Все приведённые выше рассуждения остаются верными.

Заключение
Тщательно изучив все сказанное выше, можно отметить, что никакой особой сложности задача по определению площади параллелепипеда не вызывает. Нужно всего-навсего чётко представлять все данные в материале математические понятия, абсолютно точно выучить формулы, ну и, разумеется, уметь хорошо проводить арифметические действия.
Видео
Из видео вы узнаете, как находить площать прямоугольного параллелепипеда.

