Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Naumenko
Высший разум
(856093)
11 лет назад
1. берется полупериметр. те а+в=10 для примера
2. выражается одна сторона через другую а=10-в
3. составляется выражение для площади: в*(10-в) и …
дальше вычислить что – либо затруднительно. тк не хватает информации.
НО! если периметр не очень большое число. то можно подбором найти а и в.. .
наверное. в исходном условии есть еще какие-то слова.
Вовчик
Мыслитель
(6652)
11 лет назад
например периметр 30
один прямоугольник имеет стороны 10 и 5, при этом площадь 50
другой 2 и 13, при этом площадь 26
третий 8 и 7, и площадь при этом 56
вот ведь какая хрень..
Как найти площадь, зная периметр
Площадь и периметр фигуры являются основными ее геометрическими параметрами. Их нахождение и описание с учетом известных величин составляет значительную долю в обучающем процессе. В общем смысле периметр – это длина всех границ фигуры. Для прямоугольника он равен сумме длин его сторон. А площадь представляет собой всю внутреннюю часть фигуры, измеренной в определенных единицах. Согласно свойствам фигур, а также формулам площади и периметра, можно найти соотношения между этими параметрами фигуры и выразить одно значение из другого. Для определения площади прямоугольника с известным периметром необходимо дополнительно знать одну его сторону.

Инструкция
Запишите известные параметры прямоугольной фигуры. Помимо периметра, для нахождения площади должна быть известна еще одна величина – любая сторона прямоугольника.

Согласно формуле, периметр прямоугольника находится, как сумма всех его сторон. Так как в прямоугольнике противолежащие стороны равны, можно записать формулу периметра: Р = (d+c)*2, где d и c являются прилегающими сторонами фигуры.
Площадь прямоугольной фигуры определяется произведением двух ее прилегающих сторон: S = d*c. Таким образом, зная одну из сторон можно легко найти площадь фигуры.
Подставьте в формулу периметра известные величины: одну из сторон и периметр. Выразите из полученного уравнения вторую неизвестную сторону и вычислите ее. Подставьте полученное значение в формулу площади. Вычислите искомое значение S – площади фигуры.
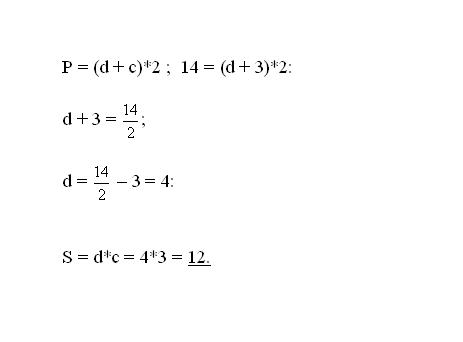
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Признаюсь, что когда я впервые увидел запрос на создание калькулятора Площадь, который звучал как «Из периметра вычислить площадь», я был несколько удивлен, ибо выглядело это несколько сюрреалистически.
Однако потом, поискав в интернете, я понял, что запрос просто не полон, и чаще всего звучит так: «Вычислите площадь прямоугольника если его периметр равен X и известно что, …» — и известны могут быть разные вещи, которые и приводят нас к решению. Например, длина одной из сторон, или соотношение сторон. Калькулятор ниже вычисляет площадь прямоугольника в зависимости от того, что еще известно кроме периметра. Посвящается школьникам.
![]()
Расчет площади прямоугольника по периметру
одна сторона больше другой на
одна сторона меньше другой на
Точность вычисления
Знаков после запятой: 2
Площадь прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.

Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:

А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».

Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
Возьмем, к примеру, такой прямоугольник:
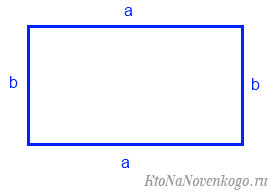
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
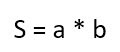
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
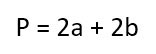
И тогда обратные расчеты выглядят вот так:
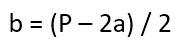
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
- Ну и второй вариант – воспользоваться сразу готовой формулой:
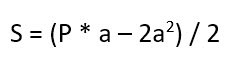
Площадь прямоугольника через диагональ
-
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
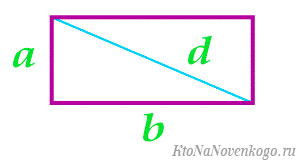
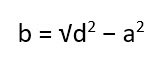
Второй вариант – опять же сразу прибегнуть к готовой формуле:
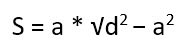
-
Если известны длина диагоналей и угол между ними.
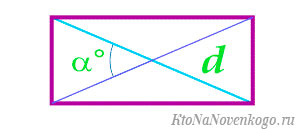
В этом случае стоит воспользоваться вот такой формулой:
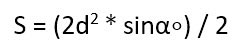
Вот и все, что нужно знать о вычислении площади прямоугольников.
