Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
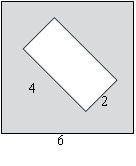
В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
2
В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны Найдите площадь прямоугольника, деленную на
3
Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
4
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Источник: Диагностическая работа 01.10.2013 Вариант МА90106
5
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Всего: 52 1–20 | 21–40 | 41–52
Добавить в вариант
Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на
В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны Найдите площадь прямоугольника, деленную на
В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, деленную на
Определите, сколько необходимо закупить пленки
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)
Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(7 вар)
Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.
Источник: Тренировочные работы. Иркутск — 2013, вариант 1.
Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его противоположных сторон, равны.
Источник: Тренировочные работы. Иркутск — 2013, вариант 3.
Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Источник: Диагностическая работа 01.10.2013 Вариант МА90106
Глубина бассейна составляет 2 метра, ширина — 10 метров, а длина — 25 метров. Найдите суммарную площадь боковых стен и дна бассейна (в квадратных метрах).
Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
Источник: Диагностическая работа 01.10.2013 Вариант МА90105
Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
Из квадрата вырезали прямоугольник (см. рис.). Найдите площадь получившейся фигуры.
Всего: 52 1–20 | 21–40 | 41–52
Здравствуйте.
Задание.
Как всегда, я предлагаю Вам самостоятельно решить задание. Чуть ниже представлены решение и ответ.
Удачи!
.
.
.
.
.
ОТВЕТ: 68
Если у Вас другой ответ, посмотрите и сравните с решением ниже.
ВАЖНО – верно соотнести название постройки и цифру, которой она обозначена (на самом деле, это вы уже сделайте в Задании №1 на настоящем экзамене).
ВАЖНО – найти длину стороны 1 клетки.
Внимательно читаем текст и соотносим название построек.
На плане же указана длина одной клетки:
Нам необходимо вычислить площадь, которую занимает жилой дом.
Друзья, очевидно, что найти площадь можно разными способами. Мы рассмотрим один из них.
Более интересный способ, по Вашему мнению, напишите мне в комментариях, обсудим.
Разобьём фигуру на 2 известные, площадь которых легко вычислить. В нашем случае, на 2 прямоугольника. И вычислим длину каждой стороны с учётом того, что длина 1 клетки=2м.
!!!! Вспомним формулу для нахождения площади прямоугольника.
Мы имеем 2 прямоугольника. НАШ ПЛАН:
1) находим площадь каждого прямоугольника отдельно.
2) складываем полученные результаты.
Выполняем:
1) Sбольшого пр.=10*6=60 квадратных метров.
Sмалень. пр.=2*4=8 квадратных метров.
2) Sдома = 60+8=68 квадратных метров.
Ответ: 68 (НАПОМНЮ!!! в бланк ответов на экзамене единицы измерения НЕ ПИШЕМ).
Всем хорошего дня!
Площадь прямоугольника, квадрата, ромба.
1. Сторона квадрата равна 10. Найдите его площадь.
2. Периметр квадрата равен 40. Найдите площадь квадрата.
3. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
4. Периметр квадрата равен 160. Найдите площадь квадрата.
5. Найдите площадь квадрата, если его диагональ равна 1.
6. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
7. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
ДЗ 8. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
9. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
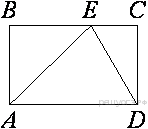
10. На стороне BC прямоугольника ABCD, у которого AB = 12 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.(см.рис.)
1. Задание 18
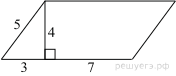 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
2. Задание 18
Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
3. Задание 18
Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
4. Задание 18 Периметр ромба равен 24, а синус одного из углов равен ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
5. Задание 18 Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
6. Задание 18 Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на ![]() .
.
7. Задание 18 Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
8. Задание 18 Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
9. Задание 18 Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
10. Задание 18 № В ромбе сторона равна 10, одна из диагоналей — ![]() , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
ДЗ 12. Задание 18 № 314870
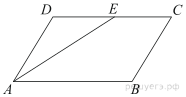
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
13. Задание 18
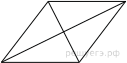 Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6.
ДЗ14. Задание 18
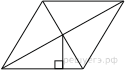 Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
15. Задание 18
Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
16. Задание 18
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
ДЗ 17.
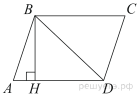 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
ДЗ 18. Задание

Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
19. Задание 18
![]() Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
20. Задание 18
Высота ![]() ромба
ромба ![]() делит его сторону
делит его сторону ![]() на отрезки
на отрезки ![]() и
и ![]() . Найдите площадь ромба.
. Найдите площадь ромба.
Материал для
подготовки к ОГЭ по математике
Прототип задания №11 по теме:
«Площади фигур»
1.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
168
2.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
Ответ:
40
3. Найдите площадь параллелограмма, изображённого
на рисунке.
Ответ:
75
4.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
28
5.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
36
6.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
Ответ:
20
7. В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Ответ:
50
8. В прямоугольном треугольнике один из катетов
равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь
треугольника.
Ответ:
50
9. Сторона равностороннего треугольника
равна 10. Найдите его площадь, делённую на ![]() .
.
Ответ:
25
10. Периметр равностороннего треугольника
равен 30. Найдите его площадь, делённую на ![]() .
.
Ответ:
25
11. Высота равностороннего треугольника
равна 10. Найдите его площадь, делённую на ![]()
Ответ:
100
12. В равнобедренном треугольнике боковая
сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите
площадь треугольника, делённую на ![]()
Ответ:
25
13. Периметр равнобедренного треугольника
равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Ответ:
12
14. Периметр равнобедренного треугольника
равен 16, а основание — 6. Найдите площадь треугольника.
Ответ:
12
15. В треугольнике одна из сторон равна 10, а
опущенная на нее высота — 5. Найдите площадь треугольника.
Ответ:
25
16. В треугольнике одна из сторон равна 10,
другая равна ![]() , а угол
, а угол
между ними равен 60°. Найдите площадь треугольника.
Ответ:
75
17. В треугольнике одна из сторон равна 10,
другая равна ![]() , а угол
, а угол
между ними равен 45°. Найдите площадь треугольника.
Ответ:
50
18. В треугольнике одна из сторон равна 10,
другая равна ![]() , а угол
, а угол
между ними равен 120°. Найдите площадь треугольника.
Ответ:
75
19. В треугольнике одна из сторон равна 10,
другая равна ![]() , а угол
, а угол
между ними равен 135°. Найдите площадь треугольника.
Ответ:
50
20. В треугольнике одна из сторон равна 10,
другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
Ответ:
30
21. В треугольнике одна из сторон равна 12,
другая равна 16, а синус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Ответ:
24
22. В треугольнике одна из сторон равна 12,
другая равна 10, а косинус угла между ними равен ![]() . Найдите площадь треугольника.
. Найдите площадь треугольника.
Ответ:
20
23. Сторона квадрата равна 10. Найдите его
площадь.
Ответ:
100
24. Периметр квадрата равен 40. Найдите площадь
квадрата.
Ответ:
100
25. В прямоугольнике одна сторона равна 10,
другая сторона равна 12. Найдите площадь прямоугольника.
Ответ:
120
26. В прямоугольнике одна сторона равна 10,
периметр равен 44. Найдите площадь прямоугольника.
Ответ:
120
27. В прямоугольнике одна сторона равна 6, а
диагональ равна 10. Найдите площадь прямоугольника.
Ответ:
48
28. В прямоугольнике диагональ равна 10, а
угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника,
делённую на ![]() .
.
Ответ:
25
29. Сторона ромба равна 5, а диагональ равна
6. Найдите площадь ромба.
Ответ:
24
30. Периметр ромба равен 40, а один из углов
равен 30°. Найдите площадь ромба.
Ответ:
50
31. Периметр ромба равен 40, а один из углов
равен 45°. Найдите площадь ромба, делённую на ![]() .
.
Ответ:
50
32. Периметр ромба равен 40, а один из углов
равен 60°. Найдите площадь ромба, делённую на ![]() .
.
Ответ:
50
33. Периметр ромба равен 24, а синус одного из
углов равен ![]() . Найдите
. Найдите
площадь ромба.
Ответ:
12
34. Периметр ромба равен 24, а косинус одного
из углов равен ![]() . Найдите
. Найдите
площадь ромба.
Ответ:
12
35. Одна из сторон параллелограмма равна 12,
а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Ответ:
120
36. Одна из сторон параллелограмма равна 12,
другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма,
делённую на ![]() .
.
Ответ:
30
37. Одна из сторон параллелограмма равна 12,
другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма,
делённую на ![]() .
.
Ответ:
30
38. Одна из сторон параллелограмма равна 12,
другая равна 5, а синус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Ответ:
20
39. Одна из сторон параллелограмма равна 12,
другая равна 5, а косинус одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Ответ:
20
40. Одна из сторон параллелограмма равна 12,
другая равна 5, а тангенс одного из углов равен ![]() . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Ответ:
20
41. Основания трапеции равны 18 и 12, одна из
боковых сторон равна ![]() ,
,
а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Ответ:
60
42. Основания трапеции равны 18 и 10, одна из
боковых сторон равна ![]() ,
,
а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Ответ:
84
43. Основания трапеции равны 18 и 12, одна из
боковых сторон равна 6, а синус угла между ней и одним из оснований равен
![]() . Найдите площадь трапеции.
. Найдите площадь трапеции.
Ответ:
30
44. Основания трапеции равны 18 и 12, одна из
боковых сторон равна 6, а косинус угла между ней и одним из оснований
равен ![]() . Найдите площадь
. Найдите площадь
трапеции.
Ответ:
30
45. Основания трапеции равны 18 и 12, одна из
боковых сторон равна 6, а тангенс угла между ней и одним из оснований
равен ![]() . Найдите площадь
. Найдите площадь
трапеции.
Ответ:
30
46. Радиус круга равен 1. Найдите его площадь,
деленную на π.
Ответ:
1
47. Найдите площадь кругового сектора,
если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите
площадь, деленную на π.
Ответ:
3
48. Найдите площадь кругового сектора,
если длина ограничивающей его дуги равна 6π, а угол сектора равен
120°. В ответе укажите площадь, деленную на π.
Ответ:
27
49. В прямоугольном треугольнике один из катетов
равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна
20. Найдите площадь треугольника, делённую на ![]() .
.
Ответ:
50
50. В прямоугольном треугольнике один из катетов
равен ![]() , острый угол, прилежащий
, острый угол, прилежащий
к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника,
делённую на ![]() .
.
Ответ:
50
51. В прямоугольном треугольнике один из катетов
равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна
20. Найдите площадь треугольника, делённую на ![]() .
.
Ответ:
50
52. В прямоугольном треугольнике один из катетов
равен ![]() , угол, лежащий
, угол, лежащий
напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника,
делённую на ![]() .
.
Ответ:
50
53. В равнобедренном треугольнике боковая
сторона равна 10, основание — ![]() , а угол, лежащий напротив основания,
, а угол, лежащий напротив основания,
равен 30°. Найдите площадь треугольника.
Ответ:
25
54. В равнобедренном треугольнике боковая
сторона равна 10, основание — ![]() , а угол, лежащий напротив основания,
, а угол, лежащий напротив основания,
равен 45°. Найдите площадь треугольника, деленную на ![]()
Ответ:
25
55. В равнобедренном треугольнике боковая
сторона равна 10, основание — ![]() , а угол, лежащий напротив основания,
, а угол, лежащий напротив основания,
равен 120°. Найдите площадь треугольника, деленную на ![]()
Ответ:
25
56. В равнобедренном треугольнике боковая
сторона равна 10, основание — ![]() , а угол, лежащий напротив основания,
, а угол, лежащий напротив основания,
равен 135°. Найдите площадь треугольника, деленную на ![]()
Ответ:
25
57. В равнобедренном треугольнике боковая
сторона равна 10, основание — ![]() , а угол, лежащий напротив основания,
, а угол, лежащий напротив основания,
равен 150°. Найдите площадь треугольника.
Ответ:
25
58. В прямоугольнике диагональ равна 10,
угол между ней и одной из сторон равен 30°, длина этой стороны ![]() . Найдите площадь прямоугольника,
. Найдите площадь прямоугольника,
деленную на ![]()
Ответ:
25
59. В прямоугольнике диагональ равна 10, а
угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите
площадь прямоугольника, деленную на ![]()
Ответ:
25
60. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, лежащий напротив
, а угол, лежащий напротив
этой диагонали, равен 30°. Найдите площадь ромба.
Ответ:
50
61. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, лежащий напротив
, а угол, лежащий напротив
этой диагонали, равен 45°. Найдите площадь ромба, деленную на ![]()
Ответ:
50
62. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, лежащий напротив
, а угол, лежащий напротив
этой диагонали, равен 120°. Найдите площадь ромба, деленную на ![]()
Ответ:
50
63. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, лежащий напротив
, а угол, лежащий напротив
этой диагонали, равен 135°. Найдите площадь ромба, деленную на ![]()
Ответ:
50
64. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, лежащий напротив
, а угол, лежащий напротив
этой диагонали, равен 150°. Найдите площадь ромба.
Ответ:
50
65. В ромбе сторона равна 10, одна из диагоналей —
10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь
ромба, деленную на ![]()
Ответ:
50
66. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, из которого
, а угол, из которого
выходит эта диагональ, равен 150°. Найдите площадь ромба.
Ответ:
50
67. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, из которого
, а угол, из которого
выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную
на ![]()
Ответ:
50
68. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, из которого
, а угол, из которого
выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную
на ![]()
Ответ:
50
69. В ромбе сторона равна 10, одна из диагоналей —
![]() , а угол, из которого
, а угол, из которого
выходит эта диагональ, равен 30°. Найдите площадь ромба.
Ответ:
50
70. В ромбе сторона равна 10, одна из диагоналей —
10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь
ромба, деленную на ![]()
Ответ:
50
71. Радиус круга равен 3, а длина ограничивающей
его окружности равна 6π. Найдите площадь круга. В ответ запишите
площадь, деленную на π.
Ответ:
9
72. Найдите площадь кругового сектора,
если длина ограничивающей его дуги равна 6π, угол сектора равен
120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
Ответ:
27
73. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
Ответ:
13
74. В равнобедренном треугольнике ![]() . Найдите
. Найдите ![]() , если высота
, если высота ![]() .
.
Ответ:
12
75. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
Ответ:
21
76. В треугольнике ![]() угол
угол ![]() равен 90°,
равен 90°, ![]() . Найдите
. Найдите ![]() .
.
Ответ:
33
77. Основания трапеции равны 4
см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите
длину большего из них.

Ответ:
5
78. Диагональ трапеции делит её среднюю линию
на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
Ответ:
6
79. Средняя линия трапеции равна 11, а меньше
основание равно 5. Найдите большее основание трапеции.

Ответ:
17
80. В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
Ответ:
20
81.  В треугольнике
В треугольнике ![]() угол
угол ![]() прямой,
прямой, ![]() . Найдите
. Найдите ![]() .
.
Ответ:
30
82.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
168
83. Найдите площадь прямоугольника, если
его периметр равен 44 и одна сторона на 2 больше другой.
Ответ:
120
84. Найдите площадь прямоугольника, если
его периметр равен 60, а отношение соседних сторон равно 4:11.
Ответ:
176
85.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
Ответ:
28
86. 
Найдите площадь
параллелограмма, изображённого на рисунке.
Ответ:
216
87.  Площадь параллелограмма ABCD равна
Площадь параллелограмма ABCD равна
56. Точка E — середина стороны CD. Найдите площадь трапеции
AECB.
Ответ:
42
88.  Боковая сторона трапеции равна 5, а один из
Боковая сторона трапеции равна 5, а один из
прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её
основания равны 3 и 9.
Ответ:
15
89.  В равнобедренной трапеции основания
В равнобедренной трапеции основания
равны 3 и 9, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Ответ:
18
90.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
Ответ:
20
91.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
92.  Найдите площадь параллелограмма, изображённого
Найдите площадь параллелограмма, изображённого
на рисунке.
93. Найдите площадь прямоугольника, если его
периметр равен 92, а отношение соседних сторон равно 3:20.
Ответ:
240
94. Найдите площадь прямоугольника, если
его периметр равен 60, а отношение соседних сторон равно 4:11.
Ответ:
176
95. Найдите площадь прямоугольника, если
его периметр равен 102, а отношение соседних сторон равно 2:15.
Ответ:
270
96. Найдите площадь прямоугольника, если
его периметр равен 58 и одна сторона на 5 больше другой.
Ответ:
204
97.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
324
98.  Найдите площадь трапеции, изображённой на
Найдите площадь трапеции, изображённой на
рисунке.
Ответ:
270
99. В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
100. Периметр равнобедренного треугольника
равен 392, а основание – 192. Найдите площадь треугольника.
