Как найти площадь прямоугольника с дробью

Математика

5 класс

Урок № 81

Площадь прямоугольника

Перечень рассматриваемых вопросов:

– формулы для расчёта площади прямоугольника и квадрата;

– определение площади прямоугольника, если его стороны выражены обыкновенными дробями.

Тезаурус

Прямоугольник– четырёхугольник, у которого все углы прямые (равны 90 градусам).

Квадрат – правильный четырёхугольник, т. е. четырёхугольник, у которого все углы равны и все стороны равны.

Обязательная литература

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Нам уже известно, что площадь прямоугольника вычисляется как произведение а и b, где а – это длина, а b – ширина прямоугольника. При этом мы считаем, что длина и ширина выражены натуральными числами и измерены в одинаковых линейных единицах.

Эта формула будет верна и при дробных а и b.

Рассмотрим прямоугольник со сторонами a = 2/3 см и b = ¾ см.

Покажем, что его площадь равна произведению 2/3 на ¾ и равна ½ см².

Достроим прямоугольник до квадрата со стороной 1 см.

Одну сторону квадрата разделим на 3 равные части, а другую на 4 равные части. Площадь квадрата равна 1 см².

S = 1 см ∙ 1 см = 1 см²

Квадрат разделен на 12 частей, соответственно площадь каждой части будет равна 1/12 см².

Прямоугольник состоит из шести таких частей, значит, его площадь будет равна

S = 6 ∙ /12 = 1/2 см²

Или, с другой стороны, площадь равна произведению сторон, а следовательно:

Таким образом, мы доказали, что площадь прямоугольника равна произведению его основания на высоту.

Как вы помните, площади различных участков могут измеряться различными единицами измерения.

Вспомним соотношения между единицами измерения площадей:

100 мм² = 1 см²

100 см² = 1 дм²

100 дм² = 1 м²

100 м² = 1 а

100 а = 1 га = 10000 м²

Вспомним, как можно смоделировать фигуру с заданной площадью.

Пусть у нас имеется ящик, полный дощечек в форме квадрата со стороной 50 сантиметров. В ящике 16 дощечек. Какую фигуру можно составить из них на участке?

Для начала определим площадь всех дощечек.

Теперь нам необходимо смоделировать фигуру с заданной площадью в 4 м².

Из этих дощечек мы можем сложить квадрат со сторонами, равными 2 м каждая.

S = 2 ∙ 2 = 4 (м²)

Или прямоугольник с длиной 1 метр и шириной 4 метра.

S = 1 ∙ 4 = 4 (м²)

Площадь каждой из этих фигур будет равна четырём квадратным метрам.

Итак, сегодня на уроке мы вспомнили формулы площади прямоугольника и квадрата, а также научились находить площадь этих фигур, если их стороны определяются дробями.

Попробуем увидеть фигуры равной площади в представленном рисунке.

Посмотрим на правильный ответ:

Зелёный треугольник – это половина от прямоугольника со сторонами из 10 и 5 клеток. Значит, площадь прямоугольника будет равна 50 клеткам, тогда площадь треугольника – 25 клеток.

Длина стороны зелёного квадрата равна 5 клеткам, поэтому его площадь также равна 25 клеткам.

Следовательно, зелёные фигуры имеют одинаковые площади.

Красные треугольники – это половинки от зелёного квадрата, а значит, их площади тоже равны.

Разбор решения заданий тренировочного модуля

Разместите нужные подписи под изображениями:

Рис. 1

Рис. 2

Варианты ответов: прямоугольник; квадрат.

Правильный ответ: при выполнении данного задания нужно использовать определения данных геометрических понятий.

1) квадрат

2) прямоугольник

Вставьте в текст нужные слова.

Площадью прямоугольника называют число, которое …. . , сколько квадратных …… содержится в …….

Слова: определяется; количество; число; показывает; единиц; квадрате; прямоугольнике.

При выполнении данного задания нужно вспомнить определение площади прямоугольника.

Правильный ответ: площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

---

Definitions

Area − The amount of surface a figure covers is its area.

For example, the perimeter measures the length of a fence going around a garden. Area measures the entire floor space that is going to be covered with a carpet.

A fraction is a number that is greater than zero but less than 1.

When two fractions that are both less than 1 are multiplied together, their product is smaller than either fraction.

In this lesson, we find areas of rectagular figures that have fractional lengths and widths.

Formula for the area of a rectangle involving fractions

If a rectangular figure has length and width of $frac{a}{b}$ and $frac{c}{d}$ where a, b, c and d are whole numbers, then the area of the rectangular figure is given by

Area = l × w = $ mathbf{frac{a}{b}}$ × $mathbf{frac{c}{d}}$ = $mathbf{frac{ab}{cd}}$ square units

Example 1:

A lake is $frac{2}{5}$ mile in length and $frac{3}{7}$ mile in width. What is the area of the lake?

Solution

Step 1:

Area of rectangle = l × w square units; l = length; w = width

Step 2:

Area of the lake = l × w = $frac{2}{5}$ × $frac{3}{7}$ = $frac{6}{35}$ square mile

Example 2:

An island in the Pacific Ocean was $frac{8}{13}$ miles wide and $frac{9}{11}$ miles long. What is the area of the island?

Solution

Step 1:

Area of rectangle = l × w square units; l = length; w = width

Step 2:

Area of the island = l × w = $frac{8}{13}$ × $frac{9}{11}$ = $frac{72}{143}$ square miles

Площадь прямоугольника. Онлайн-калькулятор

Онлайн-калькулятор площади прямоугольника поможет вам точно и быстро рассчитать или проверить расчеты по нахождению площади любого прямоугольника. Обычно площадь прямоугольника можно рассчитать двумя способами: через две стороны прямоугольника или через его диагонали. При первом способе расчета введите значения длин сторон a и b. При втором – длину диагоналей и значение угла между ними в градусах или радианах. Помимо ответа калькулятор покажет решение.

Способ расчета площади прямоугольника:

Стороны прямоугольника:

a =

b =

Рассчитать

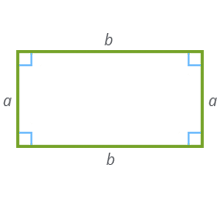
Прямоугольник – это геометрическая фигура, представляющая собой четырехугольник, у которого все углы прямые (90° ). Диагонали прямоугольника равны между собой.

Как найти площадь прямоугольника?

Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:

1) через две стороны

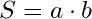
a, b – стороны

2) через диагонали и угол

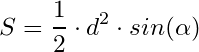
d – диагонали,
α – угол между диагоналями.