Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
Площади фигур. Основные формулы.
Площадь треугольника.
| Формула | Рисунок | Расшифровка формулы |
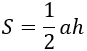 |
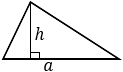 |
а – основание, h – высота, проведенная к этому основанию. Формула применима для любого треугольника. |
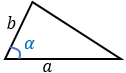 |
a, b – стороны, α – угол между этими сторонами. Формула применима для любого треугольника. |
|
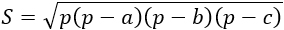 |
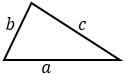 |
a, b, с – стороны, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
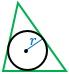 |
r – радиус вписанной в треугольник окружности, р – полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
|
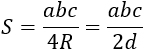 |
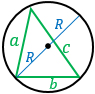 |
a, b, с – стороны, R – радиус описанной около треугольника окружности, d – диаметр описанной окружности. Формула применима для любого треугольника. |
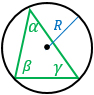 |
R – радиус описанной около треугольника окружности, α, β, γ – углы треугольника. Формула применима для любого треугольника. |
|
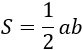 |
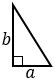 |
a, b – катеты. Формула применима для прямоугольного треугольника. |
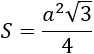 |
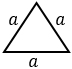 |
a – сторона. Формула применима для равностороннего (правильного) треугольника. |
Площадь квадрата и прямоугольника.
Площадь параллелограмма и ромба.
| Формула | Рисунок | Расшифровка формулы |
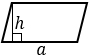 |
а – одна из сторон параллелограмма, h – высота, проведенная к этой стороне | |
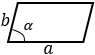 |
а, b – стороны параллелограмма, α – угол между этими сторонами | |
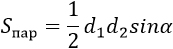 |
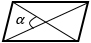 |
d1, d2 – диагонали, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны) |
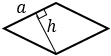 |
а – сторона ромба, h – высота, проведенная к этой стороне | |
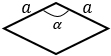 |
а – сторона ромба, α – угол между этими сторонами | |
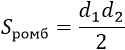 |
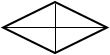 |
d1, d2 – диагонали ромба |
Площадь трапеции.
| Формула | Рисунок | Расшифровка формулы |
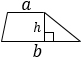 |
а, b – основания трапеции, h – высота. Формула применима для любой* трапеции. |
|
|
m – средняя линия трапеции, h – высота. Формула применима для любой трапеции. |
||
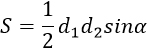 |
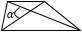 |
d1, d2 – диагонали трапеции, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции. |
*Любая трапеция – это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная 🙂
Площадь круга и кругового сектора.
Площадь многоугольника.
| Формула | Рисунок | Расшифровка формулы |
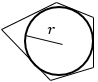 |
р – полупериметр (сумма всех сторон многоугольника, деланная на 2), r – радиус вписанной в этот многоугольник окружности. *Пятиугольник нарисован для примера. Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность. |
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
Некоторые свойства площади фигур
-
Если многоугольники равны, то они имеют равные площади.
-
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Рис. (1). Нахождение площади многоугольника
Рассмотрим, как найти площадь у разных фигур.
Площадь квадрата
Площадь квадрата равна квадрату его стороны.
, где
a
— длина стороны квадрата.
Площадь прямоугольника
Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).
, где
a
и
b
— длина и ширина.
Площадь параллелограмма равна произведению основания на высоту.
Рис. (2). Параллелограмм
,
a
(
AD
и
CD
) — основание,
h
(
BE
и
BF
) — высота.
Площадь ромба равна половине произведения его диагоналей.
Рис. (3). Ромб
Рис. (4). Треугольник
Площадь треугольника равна половине произведения основания на высоту.
, где
a
(
AD
) — основание,
h
(
BE
) — высота треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Рис. (5). Трапеция
Площадь трапеции равна половине суммы оснований, умноженной на высоту.
, где
a
(
BC
) и
b
(
AD
) — основания,
h
(
BE
) — высота.
Площадь круга и кругового сектора
Рис. (6). Круг
— площадь кругового сектора.
Более подробно ознакомиться с примерами можно здесь.
План урока:
Площадь прямоугольного треугольника
Площадь произвольного треугольника
Площадь параллелограмма
Площадь ромба
Площадь трапеции
Площадь прямоугольного треугольника
Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?
Прямоугольный треугольник можно достроить до прямоугольника:
Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что
Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.
Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:
Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.
Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:
Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:
x = 10
Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.
Ответ: 10; 20.
Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:
Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:
Подсчитаем площадь каждой из трех фигур по отдельности:
Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:
Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):
Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:
Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S1, S2 и S3:
Площадь произвольного треугольника
Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:
В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:
Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:
В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:
Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):
На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:
Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:
Итак, можно сформулировать следующее правило:
Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.
Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.
Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:
Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.
Решение.
Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что
Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:
Получили одно и то же значение, то есть площади треуг-ков равны.
В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.
Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:
Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:
Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:
Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:
Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:
Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.
Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.
Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.
Решение.
Зная ТН и РЕ, мы сможем найти площадь треуг-ка:
Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ
Величину SРЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:
Площадь параллелограмма
Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:
На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.
Опустим в параллелограмме АВСD высоты ВН и СК:
В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).
Раз они равны, то одинаковы и их площади:
Но величину S3 можно заменить на S2. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:
Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:
Задание. Найдите площадь параллелограмма, изображенного на рисунке:
Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:
Далее надо просто перемножить эти длины:
Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:
Дальше можно просто посчитать по отдельности S1, S2и S3, после чего сложить их. Попробуйте сделать это самостоятельно.
Задание. Площадь параллелограмма равна 162 см2, а одна из его высот вдвое короче основания, к которому она проведена. Найдите эту высоту и основание.
Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:
Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.
Ответ: 9 и 18.
Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.
Решение. Опустим на сторону длиной 14 см высоту:
Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:
Площадь ромба
Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.
Построим ромб и проведем в нем диагонали:
Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:
Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, SAOB:
В результате мы доказали следующее утверждение:
Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.
Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:
Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.
Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:
Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30
Ответ: 10 и 30 см.
Площадь трапеции
Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.
В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:
Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:
Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:
В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:
Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.
Решение. Это простая задача на использование формулы площади трапеции:
Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):
Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:
Считаем площадь:
Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?
Решение. Выполним построение:
Найдем острый угол трапеции. Так как CD||АВ, то
Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:
ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:
Из равенства треуг-ков следует, что
Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.
1. Формула площади равнобедренной трапеции через стороны и угол
b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):