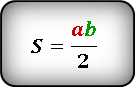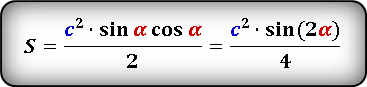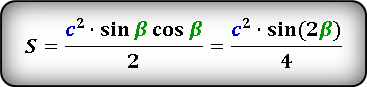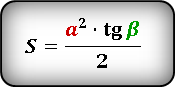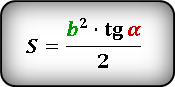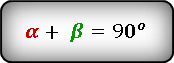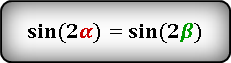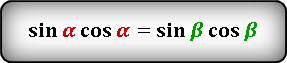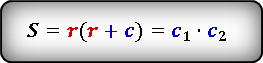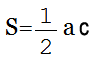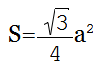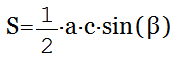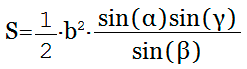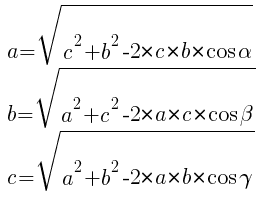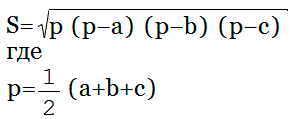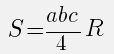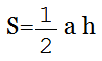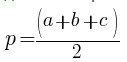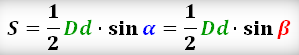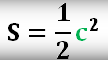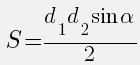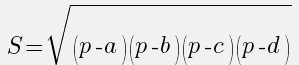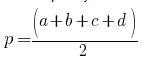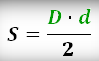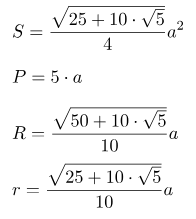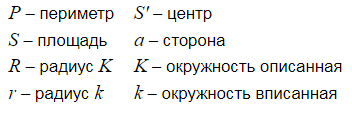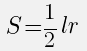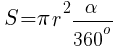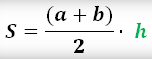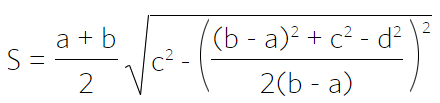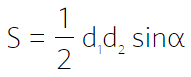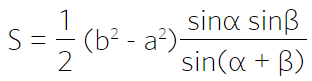Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
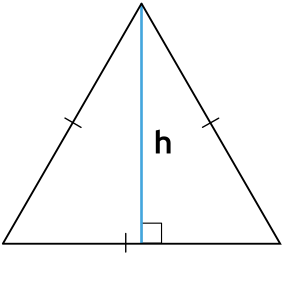
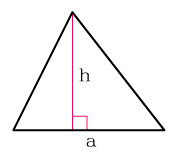
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
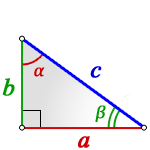
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
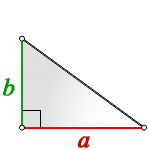
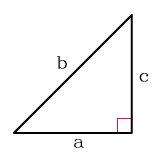
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
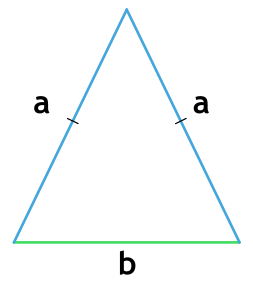
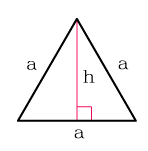
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
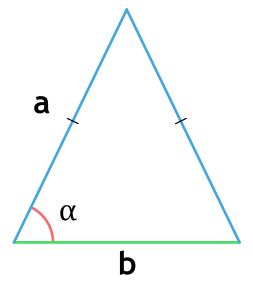
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
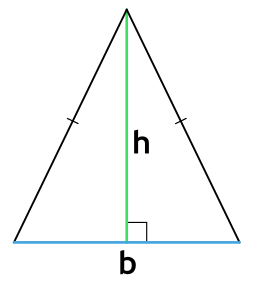
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
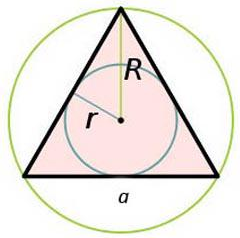
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
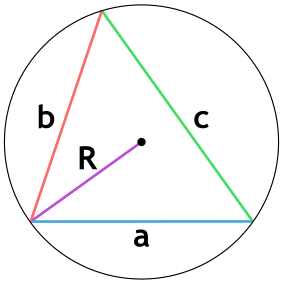
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
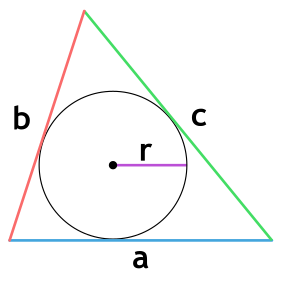
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Теория и практика по треугольникам (Часть Ⅱ)

Тригонометрия в прямоугольных треугольниках.
Что такое синус/косинус.
Таблицы Брадиса. Как пользоваться.
Теорема синусов и косинусов.
Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.
С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.
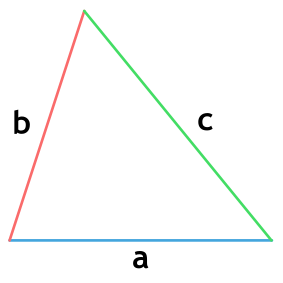
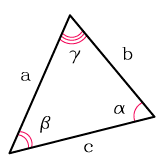
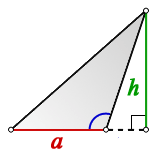
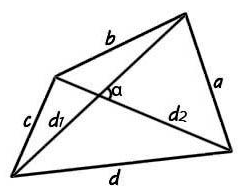
Площадь произвольного треугольника
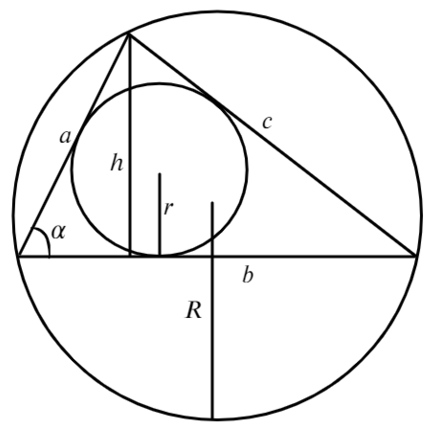
Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.
Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:
Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):
Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:
А эта формула помогает найти радиус описанной окружности для любого треугольника:
А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.
Полезные формулы для прямоугольного и равностороннего треугольника:
В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.
Эту формулу можно вывести большим количеством способов, самый простой через формулу №2
Задача №1. Дано на рисунке:
Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα
Ответ: 60
Задача №2. Дано на рисунке:
Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:
Теперь можно подставить все числа в формулу площади:
Главное — правильно определиться с формулой.
Задача №3. Дано на рисунке:
В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.
Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168
Задача №4. Дано на рисунке:
Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:
В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:
Площадь найдем по (2) формуле: S = ½absinα:
Задача №5. Дано на рисунке:
В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).
Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.
Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.
Ответ: 14,2 и 150°
Тригонометрия в прямоугольных треугольниках
В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.
Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.
Относительно угла α:
Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!
Тригонометрические функции (синус, косинус. ) задают связь между углом и длинами сторон.
Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?
Найдем sin(10°) . Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.
А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.
Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.
p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600”.
Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:
Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:
Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.
В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.
Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,
даже зная решение задачи, трудно понять, как можно было до него додуматься.
Задача №6. Дано на рисунке:
В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!
Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:
Задача №7. Дано на рисунке:
Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.
В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°
Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!
Теорема синусов и теорема косинусов
Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.
Для любого треугольника можно записать такое соотношение, это будет теорема синусов:
Запомни, что сторона относится к синусу противолежащего угла.
Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:
Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:
А что будет, если α = 90°, а cos(90) = 0? Получится:
Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.
Можно записать и для других сторон в этом же треугольнике:
Задача №8. Дано на рисунке:
Запишем теорему синусов для двух отношений:
Выразим отсюда KT:
∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:
Тогда представим 75° в виде двух табличных значений:
Аналогично выразим LT:
Ответ: 16,3 и 22,3
Задача №9. Дано на рисунке:
Найти нужно x и y. Запишем теорему косинусов для этого треугольника:
Икс выразим через игрек:
Отлично, поздравляю тебя с Elementary по геометрии!
Что нужно знать:
- Вертикальные, смежные, соответственные, накрест лежащие углы.
- Равенство и подобие треугольников.
- Что такое медиана, биссектриса, высота.
- Свойства треугольников.
- Площадь треугольников.
- Синус/косинус в треугольнике.
- Теорему синусов и косинусов.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
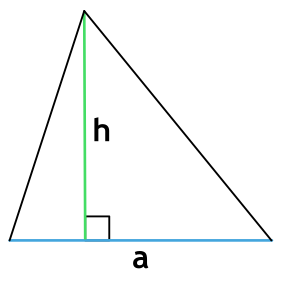
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
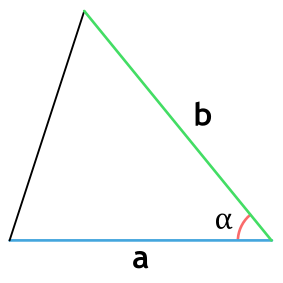
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
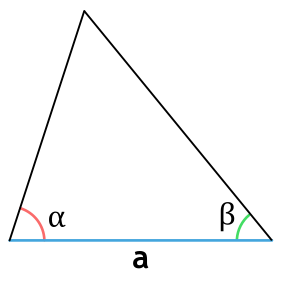
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
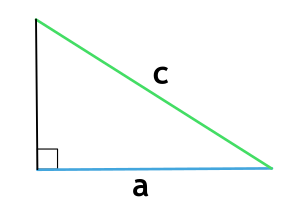
Площадь треугольника с углом 90° по двум сторонам
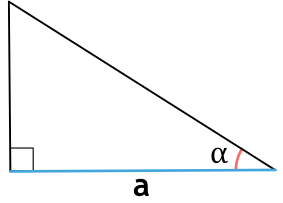
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
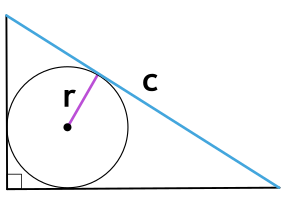
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://ik-study.ru/ege_math/tieoriia_i_praktika_po_trieughol_nikam_chast_ii_
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
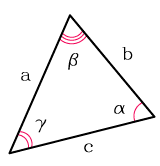
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
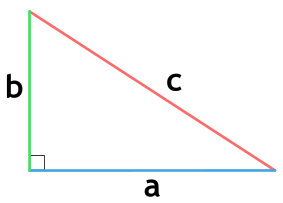
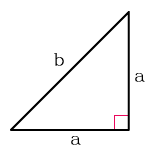
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
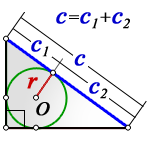
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
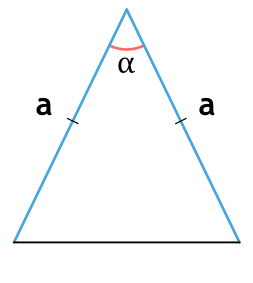
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
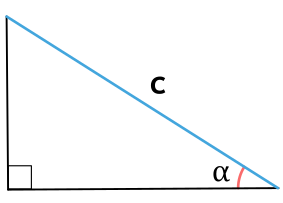
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется – гипотенуза
1. Если известны только катеты
a, b – катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c – гипотенуза
a, b – катеты
α, β – острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
c – гипотенуза
c1, c2 – отрезки полученные делением гипотенузы, точкой касания окружности
r – радиус вписанной окружности
О – центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
- Подробности
-
Опубликовано: 07 сентября 2011
-
Обновлено: 13 августа 2021
Содержание:
- Площадь треугольника
- Площадь параллелограмма
- Формула площади прямоугольника
- Площадь квадрата
- Площадь четырехугольника
- Площадь многоугольника
- Площадь ромба
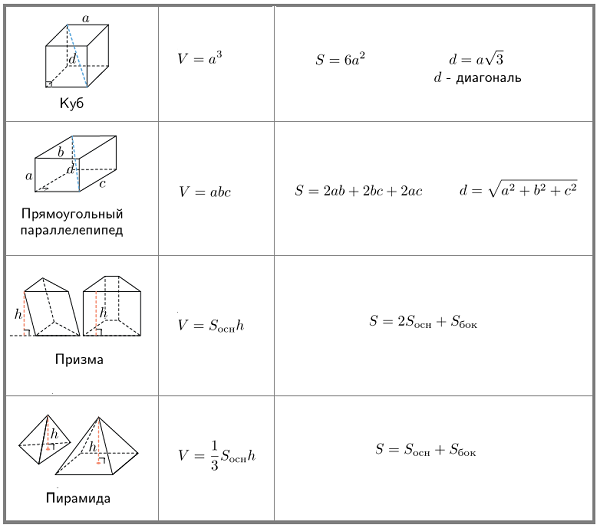
- Площадь многогранника
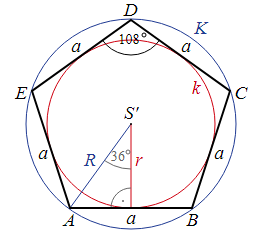
- Площадь пятиугольника
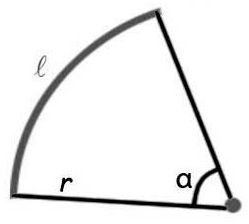
- Площадь закрашенного сектора
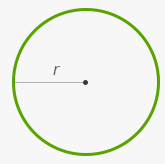
- Площадь круга
- Площадь трапеции
Площадь треугольника
Прямоугольного
Равностороннего треугольника
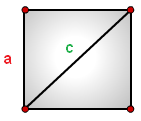
Площадь равнобедренного прямоугольного треугольника
S = a2/2
Площадь треугольника через синус
Площадь треугольника через косинус
Для нахождения площади треугольника нужно знать все стороны. По теореме косинусов квадрат неизвестной стороны равен:
Следовательно:
Далее используем формулу Герона:
Площадь треугольника через радиус описанной окружности
Произвольного треугольника
Формула Герона
Площадь треугольника через высоту
Площадь треугольника через полупериметр
Формула Герона
является полупериметром.
Площадь тупоугольного треугольника
S = ah/2
Площадь треугольника через радиус вписанной окружности
S = p×r
где p – полупериметр:
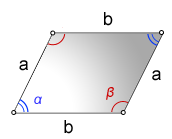
Площадь параллелограмма
Через синус
Через стороны и углы
S = a×b×sin(α) = a×b×sin(β)
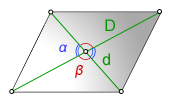
Через диагонали и угол между ними
Формула площади прямоугольника
S = a×b
Площадь квадрата
S = a2
Площадь четырехугольника
Выпуклого четырехугольника
где
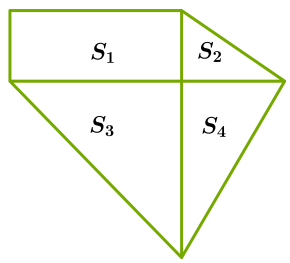
Площадь многоугольника
S = S1 + S2 + S3 + S4
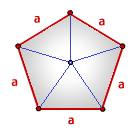
Правильного многоугольника
где n – количество сторон многоугольника.
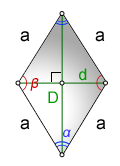
Площадь ромба
Площадь многогранника
Площадь пятиугольника
Площадь закрашенного сектора
Площадь круга
S = πr2
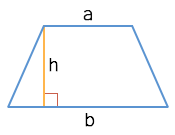
Площадь трапеции
Через основания и высоту
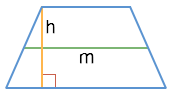
Через высоту и среднюю линию
S = hm
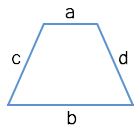
Через четыре стороны
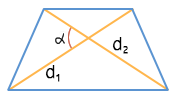
Через диагонали и угол между ними
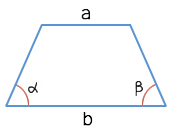
Через основания и два угла