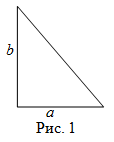Содержание:
- Формула
- Примеры вычисления площади прямоугольного треугольника
Формула
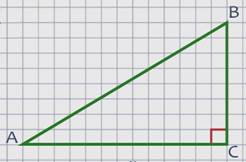
Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1),
надо найти произведение катетов
$a$ и
$b$ и поделить его на два. То есть
$$mathrm{S}_{Delta A B C}=frac{a b}{2}$$
Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.
Примеры вычисления площади прямоугольного треугольника
Пример
Задание. Найти площадь прямоугольного треугольника
$ABC$, если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
$mathrm{S}_{Delta A B C}=frac{3 cdot 4}{2}=frac{12}{2}=6$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.
Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора,
найдем второй катет заданного треугольника:
$b=sqrt{10^{2}-6^{2}}=sqrt{100-36}=sqrt{64}=8$ (см)
Тогда площадь
$S=frac{6 cdot 8}{2}=frac{48}{2}=24$ (см2)
Ответ. $S=24$ (см2)
Читать дальше: как найти площадь равнобедренного треугольника.
Содержание:
- § 1 Виды треугольников
- § 2 Прямоугольный треугольник
- § 3 Стороны прямоугольного треугольника
- § 4 Площадь прямоугольного треугольника
- § 5 Краткие итоги урока
§ 1 Виды треугольников
В этом уроке научимся находить площадь прямоугольного треугольника.
Давайте отправимся в страну «Геометрия» в город треугольников. Здесь всё треугольное: и дома, и деревья, и даже жители. На первый взгляд, эти жители все очень похожи: у них по три угла, три стороны и три вершины. Но при этом все они отличаются друг от друга. Давайте рассмотрим некоторые из них:
Этот треугольник тупоугольный,
в нем содержится тупой угол.
Это равносторонний треугольник –
у него все стороны равны.
А вот треугольник, у которого равны две стороны.
Его называют равнобедренным.
А это треугольник,
в котором угол С – прямой.
Такой треугольник называют прямоугольным.
§ 2 Прямоугольный треугольник
С прямоугольным треугольником мы познакомимся поближе.
Но сначала давайте решим задачу.
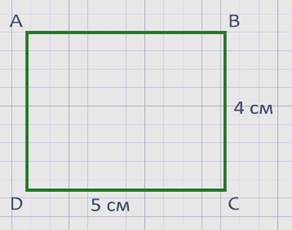
Дан прямоугольник АВСD со сторонами 5 см и
4 см. Нужно найти площадь этого прямоугольника.
Вспомним формулу нахождения площади прямоугольника.
Формула – это верное равенство, устанавливающее взаимосвязь между величинами.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину (S = a× b). Значит, S = 5 × 4 =20см2.
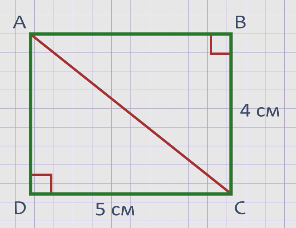
Теперь возьмём наш прямоугольник и проведём в нём диагональ АС.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника.
Мы видим, что диагональ разделила наш прямоугольник на два одинаковых треугольника. Оба эти треугольника прямоугольные, так как каждый из них содержит прямой угол.
Теперь можно легко найти площадь каждого из этих треугольников. Нужно просто площадь прямоугольника разделить пополам. Значит, площадь каждого из этих треугольников будет равна
S∆ = 20 : 2 = 10 см2.
У нас получилось, что площадь прямоугольного треугольника равна половине площади прямоугольника.
S∆ = (a × b) : 2
§ 3 Стороны прямоугольного треугольника
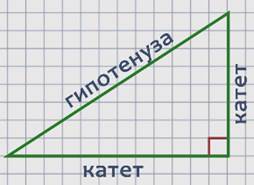
Стороны прямоугольного треугольника имеют свои названия, давайте с ними познакомимся.
Стороны прямоугольного треугольника, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла, называется гипотенузой.
Чтобы легче было запомнить, можно выучить небольшие стихи о катетах и гипотенузе.
Мы два брата-стороны, катетами названы.
Болтаем мы о том, о сём, сходясь в вершине в углу прямом.
Гипотенуза – я, особый элемент, длинней меня сторон здесь просто нет.
Меня найти нетрудно, право слово,
Лежу напротив я угла прямого.
§ 4 Площадь прямоугольного треугольника
Теперь выведем правило нахождения площади прямоугольного треугольника, зная, как называются его стороны.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
где a и b – катеты прямоугольного треугольника.
Рассмотрим нахождение площади прямоугольного треугольника на примере.
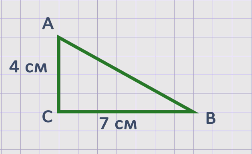
Нам дан треугольник АВС.
Сначала измерим его катеты.
Катет АС = 4 см, катет СВ = 7 см.
Вспомним правило нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
Эту формулу необходимо запомнить.
Подставим в неё вместо букв значения.
Получим:
S∆ = (4 × 7) : 2 = 28 : 2 = 14 см2.
Используя данные знания, Вы сможете вычислять площадь и других фигур, разделив их на знакомые фигуры, площадь которых Вы уже умеете вычислять.
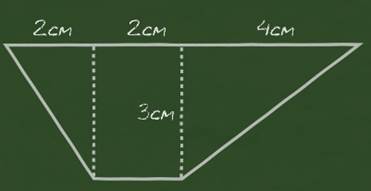
Давайте найдём площадь трапеции.
Для этого мы разделим её вертикальными линиями на прямоугольник и два прямоугольных треугольника, как показано на рисунке.
Найдём сначала площадь прямоугольника. Его длина – 3 см, ширина – 2 см.
Вспомним формулу нахождения площади прямоугольника.
Чтобы найти площадь прямоугольника, надо длину умножить на ширину S = a× b .
Выполняем первое действие:
1) 3 × 2 = 6 см2 – S прямоугольника.
Теперь находим площади треугольников. Вспомним формулу нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
где a и b – катеты прямоугольного треугольника
Найдём площадь левого треугольника, его катеты 2 см и 3 см.
2) (2 × 3) : 2 = 3 см2 – площадь левого треугольника.
Найдём площадь правого треугольника. Его катеты 3 см и 4 см.
3) (3 × 4) : 2 = 6 см2 – площадь правого треугольника.
Чтобы узнать площадь всей фигуры, надо сложить площади этих трёх фигур.
4) 6 + 3 + 6 = 15 см2 – площадь трапеции.
Ответ: площадь трапеции равна 15 см2.
§ 5 Краткие итоги урока
Подведем итоги нашего урока:
Чтобы вычислить площадь прямоугольного треугольника, необходимо:
1.Найти у треугольника катеты (это стороны, образующие прямой угол).
2.Определить их длину.
3.Вспомнить формулу нахождения площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
S∆ = (a × b) : 2
4.Подставить в формулу вместо букв их значения.
5.Вычислить значение получившегося выражения, т.е. площади.
Список использованной литературы:
- Автор конспекта: Курманаева Светлана Валентиновна
- Петерсон Л.Г. Математика. 4 класс. Часть 1./Л.Г. Петерсон. – М.: Ювента, 2014.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² – a² = ½ ⋅ b ⋅ √c² – b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² – 2² / 2 = √25 – 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b – ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b – ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 – α) = ½ ⋅ b² ⋅ tg(90 – β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Всем привет, сегодня я покажу как выводятся 4-основные формулы для нахождения площади треугольника, для понимания следующего материала нужно знать теорему синусов, площадь прямоугольника.
*UDP доказательство формулы Герона в этой статье*
Для начала поймем один частный случай(если это понимаете, пролистывайте дальше).
Площадь прямоугольного треугольника.
У нас есть прямоугольный треугольник с катетами a,b, нужно найти его площадь.
Достраиваем до прямоугольника.
Площадь такого прямоугольника будет a * b, а значит площадь прямоугольного треугольника будет 1/2 * a * b(т.е. половинка от площади прямоугольника).
Этот факт нам понадобится для доказательства первой формулы.
Площадь треугольника через основание и высоту.
Мы опустили высоту на основание a, замечаем что исходный треугольник разбился на два прямоугольный треугольника, значит посчитаем их площадь, но для начала назовём отрезки x, y , на которые высота делит основание a.
Найдем площадь 1,2 треугольника и сложим их(т.к он и состоит из этих площадей).
А теперь вот здесь выносим общий множитель за скобку.
x + y – это и есть a, => получаем формулу половина основания на высоту.
Площадь через синус угла между сторонами.
Опустим высоту на основание b и назовём её x. Посмотрим на этот прямоугольный треугольник
Нам нужно найти x, как это можно сделать если нам известен только угол альфа и гипотенуза a? Очевидно, расписать синус этого угла и выразить от туда x.
Ну и теперь используем ранее доказанную формулу “половина основания на высоту”.
Произведение всех сторон на 4 радиуса описанной окружности.
Чтобы доказать эту формулу, нужно знать теорему синусов. и помнить ранее доказанную формулу.
Выразим синус угла альфа из теоремы синусов.
Подставляем синус альфа в ранее доказанную формулу.
Вот и вся формула. Изи, не правда ли? Теперь чуть посложнее.
Площадь треугольника через полупериметр и радиус вписанной окружности.
У нас есть треугольник ABC со сторонами a,b,c , в него вписана окружность радиуса r с центром O, которая касается сторон в точках K, L, M.
Проведём радиус в точки касания и соединим вершины треугольника с центром окр.
Теперь считаем площадь вот этих трех выделенных треугольников
Площадь AOC = 1/2 r * a, AOB = 1/2 r * b, COB = 1/2 r * c.
значит площадь ABC = AOC + AOB + COB
1/2 * r выносим за скобки.
(a + b + c )/ 2 это полупериметр p.
Вот и наша формула.
Если хотите узнать доказательство формулы Герона, заходите на эту статью.
Спасибо за внимание.
Какие размеры известны:
Два катета
Катет и гиппотенуза
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Треугольник – это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.
Треугольники бывают прямоугольный, равнобедренный, равносторонний.
Катет – это прилежащая прямому углу сторона треугольника.
Гипотенуза – это сторона треугольника противолежащая прямому углу.
Формула площади прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника, необходимо знать размеры двух сторон треугольника.
Площадь прямоугольного треугольника расчитывается по формуле:
a
b
c
S = dfrac{a cdot b}{2}
- S – площадь треугольника
- a – катет
- b – катет
- c – гипотенуза
Если известены размеры только одного катета и гипотенузы, тогда площадь прямоугольного треугольника можно расчитать по формулам:
S = dfrac{a cdot sqrt{c^2 – a^2}}{2}
S = dfrac{b cdot sqrt{c^2 – b^2}}{2}
Похожие калькуляторы:
Войдите чтобы писать комментарии