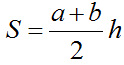Как найти площадь прямоугольного треугольника в трапеции

Сегодня продолжим тему трапеций и площадей. На этот раз надо найти площадь треугольника в этой трапеции

Достаточно много известно в трапеции, а значит должно быть много интересных способов решения. Но это не точно. Кстати, задача не самая простая, на экзамене это было бы почётное 25-е задание ОГЭ или 16-е задание профильного уровня ЕГЭ.

На что можно обратить внимание:

1. Треугольник ∆AKD — известны все стороны, можно найти площадь, синусы и косинусы углов;
2. Подобие треугольников образованных основаниями трапеции;
3. Отношение площадей треугольников образованных одной диагональю трапеции;
4. Биссектриса угла при основании — и то, что она отсекает от трапеции.

Условие

В трапеции ABCD основание AD равно √7. Диагонали АС и DB пересекаются в точке К. Известно, что AK = 1, KD = 2, ∠ВАС = ∠DAC. Найдите площадь треугольника ABC.

Подписывайтесь на канал Около ОГЭ, если еще нет. Делитесь решениями в комментариях. Удачи!

Решайте также:

🍀 Площадь прямоугольной трапеции и пропорциональные отрезки

🍀 Найти площадь трапеции, описанной около окружности

🍀 Устно: найти отношение площадей

Площадь прямоугольной трапеции найти очень просто: достаточно вспомнить, из что представляет собой эта геометрическая фигура. Трапеция состоит из двух параллельных и двух боковых сторон, причем одна из боковых сторон имеет угол в 90 градусов. Найти площадь трапеции можно по следующим формулам: модератор выбрал этот ответ лучшим [поль­зоват­ель забло­киров­ан] [179K] 7 лет назад  Площадь трапеции равна полусумме её оснований, умноженной на высоту данной трапеции: S=(( AD+ВС) :2)хВН, Высотой трапеции является любой перпендикуляр , относительно основаниям трапеции, проведенный из любой точки от одного основания трапеции до другого. Площадь равнобедренной трапеции можно найти и по формуле: S=4r:sina; в этой формуле r– это радиус вписанной в равнобедренную трапецию окружности, sina – угол при основании. Площадь трапеции равна произведению средней линии трапеции и её высоты: S=mh, где h– это высота трапеции, m– её средняя линия. Есть и ещё одна формула, по которой возможно найти площадь трапеции. В данной формуле: a и b– это основания, с и d– боковые стороны трапеции. Что такое прямоугольная трапеция? Это фигура, у которой две стороны параллельны, третья перпендикулярна первым двум, а четвёртая расположена под определённым, не прямым углом. Рисунок: На рисунке вы видите прямоугольную трапецию. Две стороны у неё параллельны (a и c). Сторона b перпендикулярна, а четвёртую сторону мы даже можем не обозначать, так как она нам не понадобится для расчётов. Теперь посмотрите, что будет, если справа достроить к четвёртой стороне два отрезка так, как изображено на рисунке красным цветом. То есть отрезки должны быть параллельны противоположной стороне трапеции. Как вы видите, получился прямоугольник большей площади, чем наша трапеция. Затем ещё проведём из правого верхнего угла трапеции вниз отрезок, перпендикулярный нижней стороне. Таким образом наш большой прямоугольник делится на два поменьше. Левый цельный, а правый – состоящий из треугольников. Площадь трапеции складывается из суммы площади левого прямоугольника и из площади треугольника: Sтрап = Sab + Sтреуг Площадь левого прямоугольника равна произведению a на b: Sab = a * b А площадь треугольника равна одной второй от площади правого прямоугольника, то есть её половине. Вертикальная сторона этого прямоугольника равна b, а горизонтальная равна разности между большей из параллельных сторон трапеции и меньшей, то есть вертикальная сторона равна c-a. Получается, что площадь правого прямоугольника равна b(c-a). Таким образом площадь треугольника равна: Sтреуг = b(c-a)/2 А искомая площадь трапеции: Sтрап = ab + b(c-a)/2 Ответ: Площадь прямоугольной трапеции равна ab + b(c-a)/2 Nonse­nse [63.5K] 7 лет назад  Вот так выглядит прямоугольная трапеция (ПТ), у неё одна из боковых сторон равна высоте и образует с основаниями прямой угол (90º): Площадь ПТ — половина суммы длин оснований, умноженная на высоту: Или произведение средней линии на высоту: Или половина произведения диагоналей на синус угла между ними: Или, если диагонали трапеции перпендикулярны, то просто, половине их произведения: Или полупериметру, помноженному на радиус вписанной окружности: Или иначе, положив что AD=a, BC=b, CD=c, и AB=h(высота)=2r(двойной радиус или диаметр вписанной окружности): Или удвоенное произведение радиуса вписанной окружности и средней линии: Galin­a7v7 [120K] 7 лет назад  Для ответа именно на этот вопрос- “как найти площадь прямоугольной трапеции АВСД “(АВ | АД) достаточно знать: 1)2 основания ВС =b и АД =а. 2)Высоту трапеции АВ=h Формула площади S прямоугольной трапеции: S = (a+b)*h/2 То есть необходимо знать или найти 3 параметра трапеции: оба основания, и боковую сторону, которая перпендикулярна обоим основаниям. Трапеция которая имеет прямые (90 градусов) углы при боковой стороне называется прямоугольной. Площадь прямоугольной трапеции равна сумме площадей прямоугольника с меньшем основанием a и высотой h и прямоугольного треугольника с основанием с и высотой h. А теперь посчитаем: площадь прямоугольника равна a*h, а площадь прямоугольного треугольника равна c*h/2 (сторона с=b-a) = (b-a)*h/2 таким образом площадь любой прямоугольной трапеции можно написать в виде: S(трапеции)=a*h+(b-a)*h/2=(2a*h+(b-a)*h)/2=h(2а+b-a)/2=h(а+b)/2. а+b у нас сумма оснований трапеции, поэтому площадь прямоугольной трапеции равна сумме оснований умноженной на половину высоты трапеции Virin­eya [16K] 7 лет назад  Трапеция – это четырехугольник с двумя параллельными друг другу сторонами, являющиеся её основаниями, а две наклонные стороны – её боковыми. Прямоугольная трапеция – это фигура, у которой хотя бы одна сторона имеет угол 90 градусов. Хотя у данной фигуры минимум 2 прямых угла; это трапеция, у которой одна сторона перпендикулярна двум основаниям. Площадь прямоугольной трапеции ( по сути, ничем не отличается от формулы вычисления площади обычной трапеции, но одна из сторон является высотой): произведение 1/2 суммы её двух оснований и высоты, которая может являться одной из боковых сторон фигуры. Определяется по формуле: S = 1/2 · (a + b) · h stalo­nevic­h [24.6K] 8 лет назад  У этой фигуры имеются две параллельные стороны (a и b), а также 2 боковые. Для решения необходимо провести высоту, или же эта будет одна из боковых сторон фигуры, которая имеет угол в 90 градусов (пусть будет h), тогда формула имеет вид. Oleg7­4 [202K] 9 лет назад  Если взять два основания А и В, которые в геометрической фигуре ” трапеция ” всегда параллельны, сложить их, потом разделить эту сумму пополам и умножить полученный результат на высоту H трапеции, то получим площадь S трапеции. Стрым­брым [372K] 9 лет назад  Как мы знаем, трапецией называется геометрическая фигура, которая образована четырьмя отрезками, два из которых параллельны между собой. Площадь трапеции определяется, как полусумма оснований, помноженная на высоту. Площадь трапеции = H (A + C) / 2 где А и С – длина каждого основания трапеции А Н – это высота Напомним, что основания – это две параллельные стороны трапеции. Высота трапеции – перпендикулярна двум основаниям. Katal­ina [24.1K] 9 лет назад  Мне, если сказать честно, для ответа на этот вопрос пришлось освежить память и покопаться в интернете. Так вот, площадь прямоугольной трапеции равна деленной пополам сумме оснований, умноженной на высоту. Гульн­ара Римов­на [43] 9 лет назад  Допустим, что основания этой трапеции а( меньшее основание )и в( большее основание), высота- h. тогда, чтобы найти s можно поступить и по- другому. S=a*h+h*(b-a)/2 nasta­sykos [7] 9 лет назад  площадь прямоугольной трапеции равна полусумме оснований умноженной на высоту трапеции Sveta­2013 [95] 9 лет назад  сумму оснований умножить на высоту и поделить пополам Знаете ответ?

Формулы площадей фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

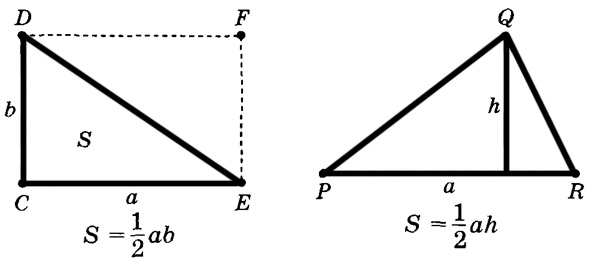
Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p – a p – b p – c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,

где a, b — стороны треугольника,
γ — угол между сторонами a и b .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R – радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r – радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Формулы площади квадрата

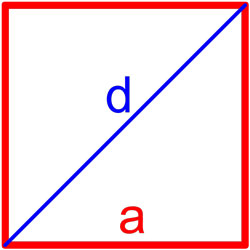
Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

где S — площадь квадрата,
a — длина стороны квадрата.

Формула площади квадрата по длине диагонали

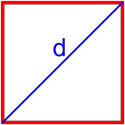
Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

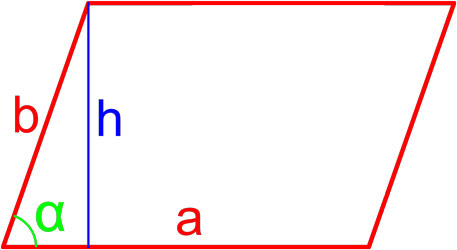
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α – угол между сторонами параллелограмма.

Формула площади параллелограмма по двум диагоналям и углу между ними

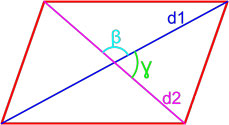
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ – угол между диагоналями параллелограмма.

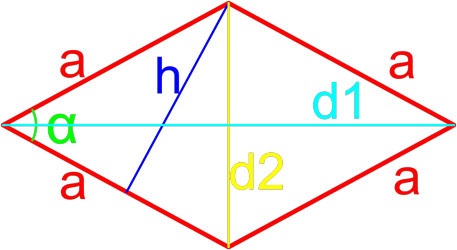
Формулы площади ромба

Формула площади ромба по длине стороны и высоте

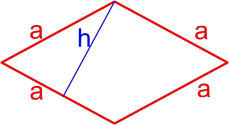
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

Формула площади ромба по длине стороны и углу

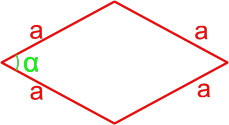
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

Формула площади ромба по длинам его диагоналей

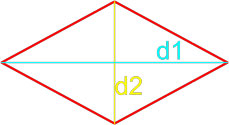
Площадь ромба равна половине произведению длин его диагоналей.

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

Формулы площади трапеции

Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).

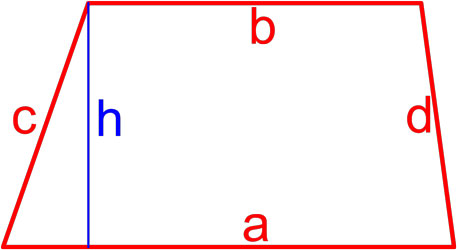
Формула Герона для трапеции

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.

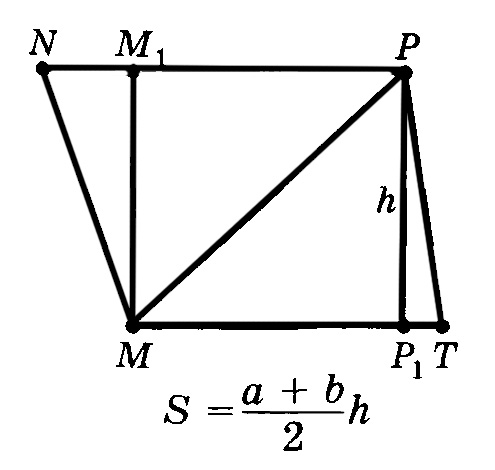
Формула площади трапеции по длине основ и высоте

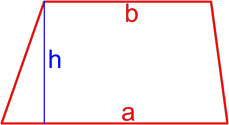
Площадь трапеции равна произведению полусуммы её оснований на высоту.

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Формулы площади дельтоида

Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

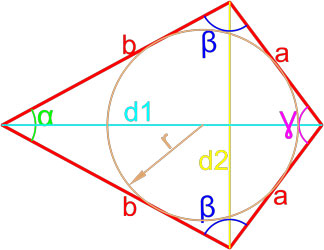
Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.

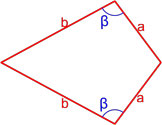
Формула площади дельтоида по равным сторонам и углу между ними

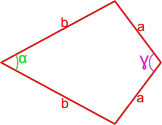
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a 2 sin γ + b 2 sin α 2 ,

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .

Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

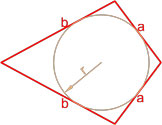
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

Формула площади дельтоида по двум диагоналям

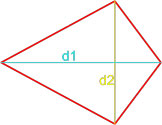
Площадь дельтоида равна половине произведения длин двух диагоналей.

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Формулы площади произвольного выпуклого четырехугольника

Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

S = d1 · d2 · sin γ 2 ,

где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади вписанного четырехугольника (формула Брахмагупты)

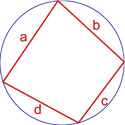
Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p – a p – b p – c p – d ,

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной окружностью

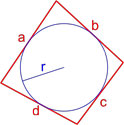
Если в четырехугольник можно вписать окружность, то его площадь равна:

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной и описанной окружностями

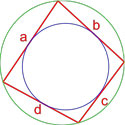
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Формулы площади круга

Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

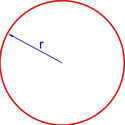S = π r 2 ,

где S — площадь круга,
r — радиус круга.

Формула площади круга через диаметр

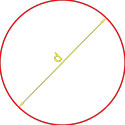
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — площадь круга,
d — диаметр круга.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

Формула площади эллипса

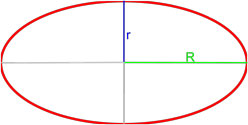
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

Равновеликие треугольники

Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.

Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.

Например, треугольники ABC и MKF — равновеликие, так как их площади равны.

Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.

Равновеликие треугольники в треугольнике

Медиана делит треугольник на два равновеликих треугольника.

Равновеликие треугольники в трапеции

При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:

1) ∆ABD и ∆ACD,

1) Проведём в треугольниках ABD и ACD высоты BH и CF.

BK=CF (как высоты трапеции), следовательно,

3)

Так как площади треугольников ABD и ACD равны (по доказанному), то и

Таким образом, треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.

Площадь треугольника, трапеции, параллелограмма

Используя рисунки выше, необходимо вспомнить, как доказывается утверждение, что «Если а является основанием треугольника, h — проведенная к нему высота, S — площадь треугольника, то

.

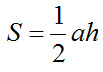
С помощью рисунка выше вспомните доказательство утверждения: «Если а и b — основания трапеции, h — ее высота, S — площадь трапеции, то

Используя данное утверждение о площади трапеции и рисунок ниже, вспомните доказательство утверждения: «Если а — основание параллелограмма, h — проведенная к нему высота, S — площадь параллелограмма, то S = ah».

[spoiler title=”источники:”]

http://belmathematics.by/shkolniku/formuly-i-teoriya/153-ploshchad-treugolnika-trapetsii-parallelogramma

[/spoiler]

Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.

I. Площадь трапеции равна произведению полусуммы оснований на высоту.

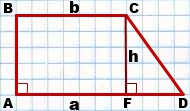Площадь прямоугольной трапеции ABCD,

AD∥BC,

   

равна

   

Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть

   

Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):

   

II. Площадь трапеции равна произведению средней линии на высоту.

Если MN — средняя линия прямоугольной трапеции ABCD,

   

то площадь

   

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:

   

III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

Для прямоугольной

трапеции

ABCD,

AD∥BC,

   

Так как sin(180º-α)=sin α, то также 

   

Если AC=d1, BD=d2, ∠COD=φ, то

   

В частности, если диагонали трапеции перпендикулярны, то

   

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

   

Так как в трапецию можно вписать окружность, то

AD+BC=AB+CD=p. Следовательно,

   

или

   

Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:

   

   

Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии.  Формула

   

Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.

   

или

   

Укажите размеры:

Основание 1

Основание 2

Боковая сторона (прямая)

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Трапеция – это четырёхугольник у которого две противоположные стороны параллельны и не равны между собой. Параллельные стороны трапеции называются основаниями, а две другие стороны называются боковыми.

Основания трапеции – это две параллельные противоположные стороны.

Высота трапеции – это прямой отрезок проведённый от центра до границы круга. В прямоугольной трапеции высота равна боковой стороне с прямым углом.

Бывают прямоугольная, равнобедренная и неравнобедренная трапеции.

Формула площади трапеции

Чтобы посчитать площадь прямоугольной трапеции, необходимо знать размеры её оснований и боковой стороны с прямым углом.

Площадь прямоугольной трапеции расчитывается по формуле:

a
b
h

S = dfrac{a + b}{2} cdot h

• S – площадь трапеции
• a – основание трапиции
• b – основание трапеции
• h – боковая сторона с прямым углом

---

Похожие калькуляторы:

Войдите чтобы писать комментарии