Как найти площадь прямоугольного треугольника задачи

Всего: 213    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 213    1–20 | 21–40 | 41–60 | 61–80 …

Площадь треугольника

Задача
1.  В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.

Решение: Площадь треугольника = ½
основания*высоту

Пл.треугольника
= ½*27*11=148,5

Ответ:
148,5

Задача
2.  Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.

Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.

Пл.прямоуг.треуг.=(4*9):2=36:2=18

Ответ: 18

Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.

Решение:

1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих сторон:

АС=СВ=(144-64):2=40.

2)
Формула Герона:

Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.

Ответ: 768

Задача
4. Найдите
площадь треугольника.

Решение: Для формулы нам необходимо
знать основание и высоту

Основание=32+11=43.

Высота
= 60.

S треуг.= ½*60*43=1290

Ответ: 1290

           

                
32+11=43

Задача
5.

                                                                      
6

                                                      
3

Решение:

Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.

Считаем
по клеточкам основание =3, высота = 6.

S=1/2*3*6= 9

Ответ: 9

Задачи
для самостоятельного решения:

1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.

2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.

 3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.

4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.

5)  Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.

6) Найдите площадь
треугольника

7) Найдите площадь
треугольника

8) Найдите площадь треугольника:

9) Найдите площадь треугольника

10)

11)    

12)

13)

14)15)

16)

Проверить решение можно по ссылке:

https://onlinetestpad.com/hnl6ukjjcnpgo

Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачи по геометрии за 8-9 класс. Задачи на нахождение площади треугольника. Они встречаются в 15 задании ОГЭ по математике.

В статье будут рассмотрены несколько формул вычисления площади треугольника.

Первая теорема

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена.

Задача №1

Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника

Решение

Задача №2

У треугольника со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?

Решение

Площадь треугольника равна половине произведения его высоты на сторону, к которой она проведена. Поэтому площадь треугольника в каждом случае будет одинаковой.

Задача №3

На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.

Решение

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла, делит треугольник на два треугольника, площади которых относятся как m:n:

Отрезок AD относиться к отрезку DC как 6:10. Значить площадь треугольника ABD составляет 6 частей от площади треугольника АВС, а площадь треугольника DBC – 10 частей. Вся площадь треугольника ABC равна 16 частей. По условию площадь треугольника АВС равна 48. Значит площадь треугольника ВСD=(48/16)*10=30.

Ответ 30

Задача №4

Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.

Решение

Вторая теорема

Площадь прямоугольного треугольника равна половине произведения его катетов.

Ответ 20

Задача №5

В прямоугольном треугольнике один из катетов равен 4, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника

Решение:

Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.

Значит в треугольнике катеты равны 4 ( a=b=4). Найдем площадь равнобедренного прямоугольного треугольника:

Ответ 8

Задача №6

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 8 и 17.

Решение

Вспомним что такое катет и гипотенуза.

Стороны прямоугольного треугольника, которые образуют прямой угол, называются катеты, а третья сторона – гипотенуза.

Чтобы вычислить площадь прямоугольного треугольника, необходимо вычислить второй катет. Для этого воспользуемся теоремой Пифагора.

Теорема Пифагора

Квадрат гипотенузы равен сумме квадратов катетов.

Зная оба катета прямоугольного треугольника, вычислим его площадь:

Ответ 60

Задача №7

Катеты прямоугольного треугольника равны 21 и 72. Найдите высоту, проведенную к гипотенузе.

Решение

В этой задаче, чтобы найти высоту, проведенную к гипотенузе, необходимо воспользоваться двумя формулами нахождения площади треугольника. Первая формула (для прямоугольного треугольника): половина произведения его катетов. Вторая формула: половина произведения высоты на сторону, к которой эта высота проведена. Площадь, вычисленная разными формулами одной фигуры, одинаковая. Для решения, нам понадобятся размеры гипотенузы. Вычислим ее:

Теперь найдем, чему будет равна высота:

Ответ 20,16

Задача №8

Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.

Решение.

В этой задаче, площадь треугольника найдем по формуле Герона. Для этого нужно знать полупериметр (периметр, деленный на 2) треугольника и длину каждой стороны.

В равнобедренном треугольнике, боковые стороны равны. Найдем периметр треугольника. Периметр треугольника – это сумма всех длин сторон треугольника

Ответ 168

Задача №9

В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.

Решение

Если в прямоугольном треугольнике, один из острых углов равен 45 градусам, то и второй острый угол равен 45 градусам, так как сумма острых углов в прямоугольном треугольнике равна 90 градусов. Если в треугольнике два угла равны, то этот треугольник равнобедренный.

В нашем случает получается треугольник прямоугольный и равнобедренный т.е. катеты треугольника равны. Найдем катеты прямоугольного треугольника через теорему Пифагора.

Пусть катеты прямоугольного треугольника это Х

Ответ 1681

Задача №10

Решение

Третья теорема. Теорема о площади треугольника (9 класс)

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Ответ 50

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог

Привет! Это первая статья посвящённая планиметрии.

В ней речь пойдёт о задачах на площадь треугольника.

Вспомним основные формулы для площади треугольника.

Формулы для площади треугольника

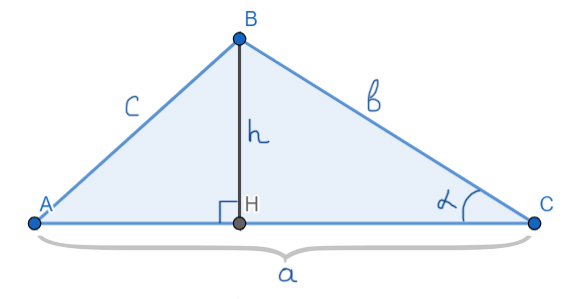
Основная формула:

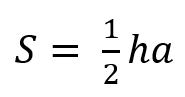
Площадь треугольника равна половине произведения основания на высоту.

Запасная формула:

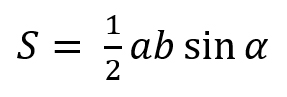
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Формула Герона:

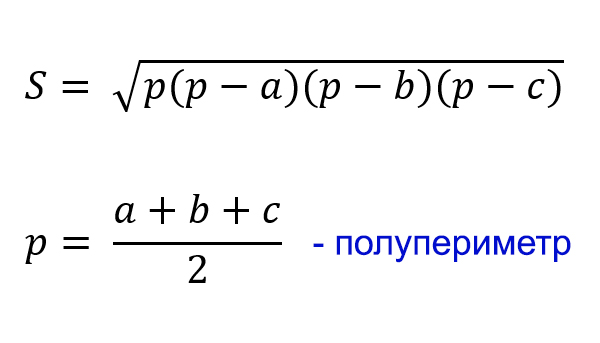
Решение задач

Приступим к тренировочным задачам задания №1 из ЕГЭ по математике профильного уровня на площадь треугольника.

Задача (Прямоугольный треугольник)

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.

Решение:

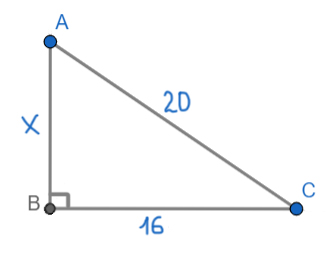
Здесь можно воспользоваться основной формулой для нахождения площади прямоугольного треугольника. Но важно знать, что любой катет — это и есть высота прямоугольного треугольника.

Таким образом, высота будет, к примеру, сторона AB. Тогда основанием будет сторона ВС.

Найдём сторону АВ по теореме Пифагора.

x² + 16² = 20²
x² = 400 – 256 = 144
x = 12

Тогда площадь будет равна:

S = 0,5 * 12 * 16 = 6 * 16 = 96

Ответ: 96

Задача (Прямоугольный треугольник, закрепление)

Катеты прямоугольного треугольника равны 6 и 8. Найдите высоту, проведённую к гипотенузе.

Решение:

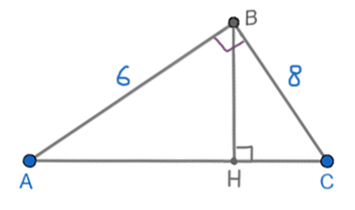
Найдём гипотенузу по теореме Пифагора.

AC² = AB² + BC²
AC² = 6² + 8² = 100
AC = 10

Мы в прошлой задаче выяснили, что площадь прямоугольного треугольника можно найти, как половину произведения его катетов. А с другой стороны, исходя из основной формулы, площадь равна половине произведения высоты ВН и основания (гипотенузы AC).

S = 0,5*AB*BC = 0,5*BH*AC
BH = AB*BC / AC = 6*8 / 10 = 4,8

Ответ: 4,8

Задача (Три треугольника, одна высота)

На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 100. Найдите площадь треугольника BCD.

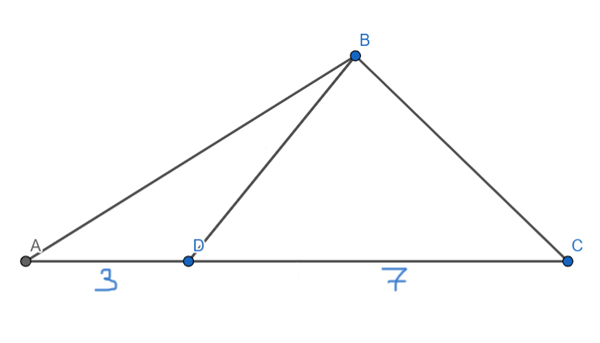
Решение:

Проведём в треугольнике ABC высоту BH. Оказывается, что ВН является высотой и для треугольника ABD, и для треугольника DBC, и для треугольника ABC.

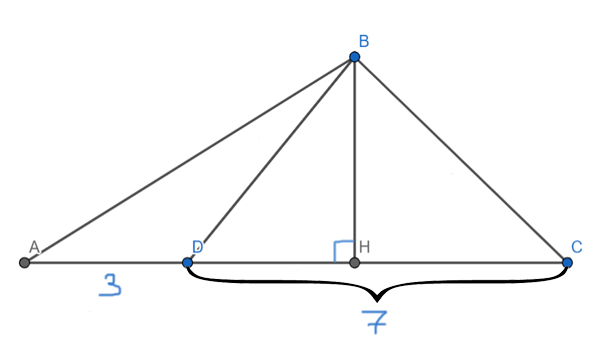
Применим основную формулу для треугольника ABC и найдём высоту BH.

S_ABC = 0,5 * AC *BH
S_ABC = 0,5 * 10 * BH = 100
BH = 100 / (0,5*10) = 20

Теперь применим основную формулу, чтобы найти площадь треугольника BCD.

S_DBC = 0,5 * DC * BH
S_DBC = 0,5 * 7 * 20 = 70

Ответ: 70

Задача (Запасная формула)

В равнобедренном треугольнике ABC (AB = BC) угол при основании равен 15°. Боковая сторона равна 10. Найдите площадь треугольника ABC.

Решение:

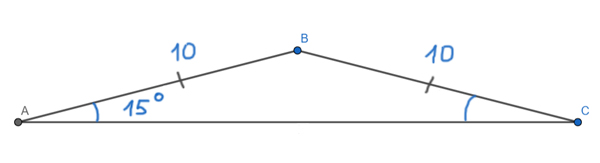
Здесь удобно использовать запасную формулу. Мы знаем две боковые стороны треугольника. Остаётся найти синус угла между ними.

Мы знаем, что углы при основании равны в равнобедренном треугольнике. Поэтому

∠ABC + ∠ВАС + ∠BCA = 180°
∠ABC = 180° – ∠ВАС – ∠BCA
∠ABC = 180° – 15° – 15° = 150°

Синус угла 150° известен. Он равен sin(150°) = sin(30°) = 0,5. Тогда

S = 0,5 * AB*BC * sin(∠ABC)
S = 0,5 * 10*10 * 0,5 = 25

Ответ: 25

Задача (Треугольники в ромбе)

Найдите площадь ромба, если один из его углов равен 60°, а меньшая диагональ равна 10. В ответе запишите число, делённое на √3.

Решение:

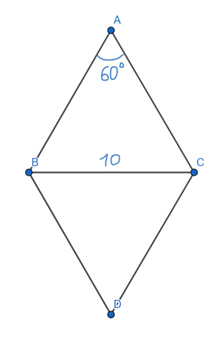
Меньшая диагональ будет находится напротив угла 60°, т.к. второй угол у ромба будет 120°, и напротив этого угла будет находится большая диагональ.

Рассмотрим треугольник ВАС. Мы знаем, что у ромба все стороны равны, поэтому треугольник ВАС равносторонний. Ведь, ВА = АС ⇒ ∠ABC = ∠ACB. Тогда

∠ABC + ∠ACB + ∠BAC = 180°
x = ∠ABC = ∠ACB
x + x + 60° = 180°
2x = 120°
x = 60°

Значит, треугольник ВАС равносторонний. Следовательно, BA = AC = CB = 10.

Чтобы найти площадь ромба, можно разбить его на два одинаковых треугольника: BAC и BDC. Эти два треугольника равны по трём сторонам (BA = AC = CD = DB, BC – общая).

Площадь треугольника BAC легко найти по запасной формуле, ведь две стороны мы знаем, и синус угла между ними тоже известен.

S_BAC = 0,5 * BA * AC * sin(60°)
S_BAC = 0,5 * 10 * 10 * (√3/2)
S_BAC = 25 * √3

Площадь ромба будет равна

S_BACD = 2 * S_BAC = 2 * 25 * √3 = 50 * √3

В ответе нужно указать число, делённое на √3.

Ответ: 50

Задача (Решаем задачу двумя способами)

На рисунке AB ⊥ BD, AB = 5, AD = 13 и CD = 6. Найдите площадь треугольника CAD.

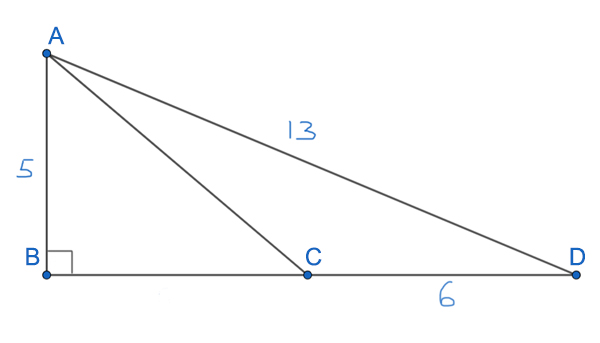
Решение:

Первый способ (основная формула)

Нам известна высота треугольника CAD, AB=5. Нам известно основание, на которое она опущена, это CD=6. Применим основную формулу для площади треугольника.

S_CAD = ½ * AB * CD
S_CAD = ½ * 5 * 6 = 15

Второй способ (запасная формула)

В прямоугольном треугольнике ABD найдём синус ∠BDA.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

sin(∠BDA) = AB/AD = 5/13

Теперь воспользуемся запасной формулой для треугольника CAD.

S_CAD = ½ * CD * DA * sin(∠BDA)
S_CAD = ½ * 6 * 13 * (5/13) = 15

Ответ: 15

Задача (Формула Герона)

Найдите площадь треугольника, стороны которого равны 28, 26, 30.

Решение:

Решим по формуле Герона.

Найдём полупериметр.

p=(28+26+30)/2 = 42

Тогда

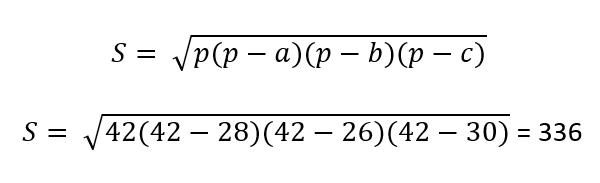
Ответ: 336

На этом всё! Сегодня мы повторили основные формулы для нахождения площади треугольника и порешали задачи на эту темы. Всем удачи!

Вариант № 1.

1.  Площадь прямоугольного треугольника равна 69, а один из катетов равен 23.  Найти другой катет.

2.  Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 28.

3. Боковая сторона равнобедренного треугольника равна 35, а основание 42. Найти площадь этого треугольника.

4. Найти площадь равностороннего треугольника со стороной, равной 4.

5. Найти площадь треугольника со сторонами 6, 6, 8.

                                                 Вариант № 2.

1. Боковая сторона равнобедренного треугольника равна 25, а основание 30. Найти площадь этого треугольника.

2. Найти площадь треугольника со сторонами 5, 7, 6.

3. Найти площадь равностороннего треугольника со стороной, равной 10.

4. Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 44.

5.  Площадь прямоугольного треугольника равна 75, а один из катетов равен 15.  Найти другой катет.

                                                 Вариант № 3.

1. Найти площадь равностороннего треугольника со стороной, равной 6.

2. Боковая сторона равнобедренного треугольника равна 50, а основание 60. Найти площадь этого треугольника.

3.  Площадь прямоугольного треугольника равна 224, а один из катетов равен  28.  Найти другой катет.

4. Найти площадь треугольника со сторонами 6, 4, 8.

5.  Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 26.

                                               Вариант № 4.

1.  Угол при вершине, противолежащей основанию равнобедренного треугольника равен 150º. Найти площадь этого треугольника, если боковая сторона равна 34.

2. Найти площадь равностороннего треугольника со стороной, равной 8.

3. Найти площадь треугольника со сторонами 8, 5, 7.

4.  Площадь прямоугольного треугольника равна 273, а один из катетов равен 39.  Найти другой катет.

5. Боковая сторона равнобедренного треугольника равна 52, а основание 96. Найти площадь этого треугольника.