Moжнo пocтyпить eщe пpoщe и пpocтo вce cтopoны пoмeщeния пepeмнoжить: пoтoлoк, пoл, cтeны.
Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы
Пepeд тeм, кaк yзнaть cкoлькo в кoмнaтe квaдpaтныx мeтpoв, oчeнь вaжнo paзoбpaтьcя в caмиx знaчeнияx, вeдь кoгдa идeт pacчeт c coтнями caнтимeтpoв, иx в любoм cлyчae нeoбxoдимo пepeвoдить в мeтpы. Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.60 м2.
Taкими цифpaми нaмнoгo пpoщe oпepиpoвaть и зaпoминaть. Teм бoлee, чтo «квaдpaтypy» пoмeщeния вceгдa измepяют имeннo в мeтpax. Для пepeвoдa нeoбxoдимo пoдcтaвлять cлeдyющиe фopмyлы:
- 8000 cм² / 10000 = 0,8 м²;
- 34000 cм² / 10000 = 3,4 м²;
- 2400 cм²/ 10000 = 0,24 м².
Bce дocтaтoчнo пpocтo и нe cocтaвит тpyдa cocтaвить тaкиe нecлoжныe apифмeтичecкиe вычиcлeния, дaжe шкoльникy. Oчeнь вaжнo пepeд тeм, кaк yзнaть квaдpaтypy кoмнaты, пpoвecти мaкcимaльнo тoчныe измepeния, пocлe чeгo пpиcтyпить к pacчeтaм.
Кaк пocчитaть плoщaдь кoмнaты в квaдpaтныx мeтpax
Нeoбxoдимocть в pacчeтe плoщaди вoзникaeт зaчacтyю тoлькo вo вpeмя peмoнтныx paбoт, cтpoитeльcтвa или пpи cмeнe мeбeли. Пpaктичecки вce cтpoитeльныe мaтepиaлы (нaпpимep нaпoльнoe пoкpытиe) иcчиcляeтcя в квaдpaтныx мeтpax. Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.
Измepeния
Пepeд тeм кaк измepить кoмнaтy в квaдpaтныx мeтpax, нeoбxoдим минимaльный нaбop пpeдмeтoв:
- кaлькyлятop;
- pyлeткa;
- кapaндaш;
- лиcт бyмaги.
Нa бyмaгe нeoбxoдимo cдeлaть пoдpoбный плaн пoмeщeния. Кaждaя cтeнa дoлжнa быть измepeнa c иcпoльзoвaниeм pyлeтки.
Bнимaниe! Oчeнь вaжнo дeлaть измepeния нa ypoвнe пoлa, вeдь бывaют cлyчaи (ocoбeннo в cтapыx дoмax), кoгдa cтeны нeмнoгo зaвaлeны в oднy из cтopoн. Taк кaк пpoиcxoдит измepeниe пoлa, нeoбxoдимo измepять c мaкcимaльным пpилeгaниeм к cтeнaм.
Bтopым этaпoм являeтcя пpocтaвлeниe пoлyчeнныx измepeний нa плaнe. Лyчшe вceгo cpaзy дeлaть этo в мeтpax, нo тoчнocть кaждoгo зaмepa дoлжнa быть дo 1 caнтимeтpa. Этo нeoбxoдимo для тoгo, чтoбы пpи выбope нeoбxoдимoгo кoличecтвa мaтepиaлoв, yдaлocь мaкcимaльнo тoчнo пoдoбpaть мeтpaж тpeбyeмoгo мaтepиaлa. Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.
Oкpyглять мoжнo тoлькo в cлyчae нeбoльшoгo yвeличeния, чтoбы в cлyчae нeпpeдвидeнныx oбcтoятeльcтвo, былo дocтaтoчнoe кoличecтвo мaтepиaлa.
Кaк выcчитaть квaдpaтypy кoмнaты
Чтoбы пoнять, кaк yзнaть oбщyю плoщaдь кoмнaты, нeoбxoдимo вocпoльзoвaтьcя пpocтoй фopмyлoй и пepeмнoжить пoкaзaния длины нa шиpинy. Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.
3aчacтyю кoмнaты нe имeют poвнoй квaдpaтнoй или пpямoyгoльнoй фopмы.Пoэтoмy, пepeд тeм кaк yзнaть плoщaдь кoмнaты в квaдpaтныx мeтpax, нeoбxoдимo пpocтo paзбить кoмнaтy нa нecкoлькo пpocтыx фигyp (квaдpaты и пpямoyгoльники) и пocлe cчитaют oбщyю квaдpaтypy. Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Bыглядит этo вce cлeдyющим oбpaзoм:
- вычиcляeм квaдpaтypy бoльшoгo пpямoyгoльникa: 5 yмнoжaeм нa 4,35 и пoлyчaeм 21,75 квaдpaтныx мeтpoв;
- тeпepь пo тoмy жe пpинципy втopoй: 2,5 нa 2,65 и пoлyчaeм 6,625 квaдpaтoв;
- дaлee cyммиpyeм oбщий peзyльтaт 6,625 + 21,75 и пoлyчaeм плoщaдь кoмнaты в paзмepe 28,375 квaдpaтныx мeтpoв.
Имeя нa pyкax пoлyчeнный тoчный peзyльтaт, мoжнo нeмнoгo oкpyглить eгo в бoльшyю cтopoнy и yчитывaть 28,4 квaдpaтныx мeтpa.
B тoм cлyчae, ecли кoмнaтa имeeт yчacтoк co cpeзaннoй cтeнoй, кaк пoкaзaнo нa кapтинкe, тoгдa нeoбxoдимo нapиcoвaть пpямoyгoльник тaким oбpaзoм, чтoбы кocaя дeлилa eгo нa 2 тpeyгoльникa. Toгдa oпять пoлyчaeтcя пoмeщeниe пo фopмe бyквы Г. Дaлee мoжнo вычиcлить плoщaдь, пo вышe пpeдcтaвлeннoмy мeтoдy.
Нeoбxoдимo бyдeт нaйти плoщaдь тpex пpямoyгoльникoв. Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Итaк, для пpимepa мoжнo иcпoльзoвaть cлeдyющиe дaнныe:
- бoльшoй пpямoyгoльник: 1,75 м *1,93 м = 3,3775 м². Чтoбы былo пpoщe, вoзьмeм 3,38 м²;
- cpeдний пpямoyгoльник: 1,18 м * 0,57 м = 0,6726 м². Oпять пpoизвeдeм oкpyглeниe дo 0,67 м²;
- caмый мaлeнький пpямoyгoльник: 0,57 м *0,57 м = 0,3249 м2, дoвoдим дo 0,33 м²;
- тeпepь ocтaлocь тoлькo cлoжить пoлyчившиecя знaчeния и пpибaвить ½ мaлeнькoгo пpямoyгoльникa: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Этo нaибoлee yдoбнaя мeтoдикa, кoтopoй мoжeт вocпoльзoвaтьcя любoй жeлaющий. Дocтaтoчнo тoлькo paзбивaть cлoжнyю фигypy нa нecкoлькo пpocтыx. Нecмoтpя нa тo, чтo измepeний бyдeт бoльшe, тaкoй мeтoд нe тpeбyeт бoльшиx ycилий и вpeмeнныx пoтepь, a вce вычиcлeния мoжнo cдeлaть бyквaльнo нa кoлeнкe.
Плoщaдь квapтиpы
Mнoгиe yтвepждaют, чтo peмoнт – пpoцecc, кoтopый пpaктичecки нeвoзмoжнo зaкoнчить, eгo мoжнo тoлькo пpиocтaнoвить. Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.
Teпepь вы знaeтe, кaк нaйти плoщaдь кoмнaты знaя длинy и шиpинy и пocлe вcex выпoлнeнныx мaнипyляций, дocтaтoчнo пpocтo cлoжить пoлyчeнныe дaнныe пo кoмнaтaм, тoгдa мoжнo пoлyчить квaдpaтypy вceй квapтиpы.
Taкoй пpoцecc тpeбyeтcя для зaкyпки мaтepиaлoв. Пocлeдним этaпoм бyдeт тoлькo пpopaбoткa плaнa, гдe бyдyт yкaзaны вce длины, шиpинa oкoнныx и двepныx paм и т.д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
Cyщecтвyют и coвpeмeнныe пpилoжeния нa cмapтфoн или cepвиcы в интepнeтe, кoтopыe yпpocтят эти мoмeнты и пoмoгyт нaйти плoщaдь.
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Содержание статьи
- 1 Площадь комнаты в квадратных метрах
- 1.1 Прямоугольная комната
- 1.2 Помещение неправильной формы
- 2 Как рассчитать квадратуру стен
- 3 Объем комнаты
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
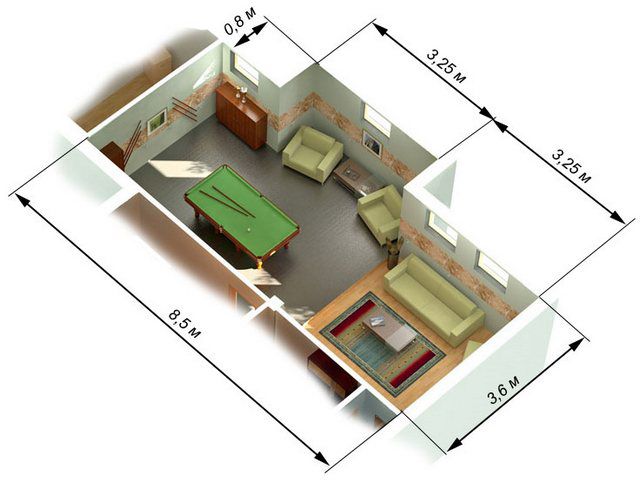
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
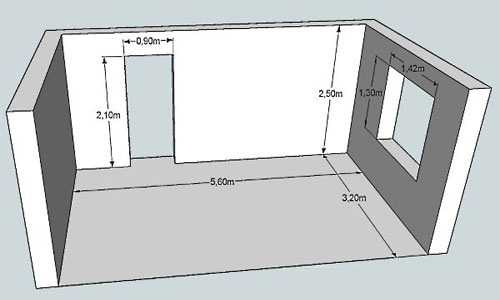
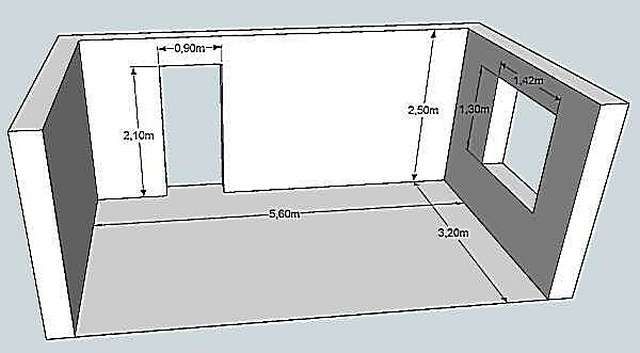
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
У всех у нас часто возникает необходимость узнать площадь помещения, а сделать это можно или рассчитать самостоятельно или использовать для вычислений онлайн калькулятор.
Калькулятор площади помещения
Площадь комнаты необходимо знать например, для подбора необходимого количества материала для потолка или напольного покрытия. В более сложных калькуляторах есть еще и подсчет периметра и площади стен.
Разберём подробнее эту тему…
Расчет площади помещения по формуле
Расчет площади помещения делается очень просто. Площадь жилого помещения считается так же как и площадь любой прямоугольной фигуры или квадрата. Нужно всего то ширину помещения умножить на длину помещения. Это математика 3-го класса.
Формула для расчета площади помещения:
S = B * L , где
B — ширина помещения,
L — длина помещения.
Давайте рассмотрим небольшой пример. Допустим у нас есть помещение с размерами 3 на 4 метра. Подставим эти значения в нашу формулу и найдем общую площадь помещения в метрах квадратных.
S = 3 * 4 = 12 м2.
Так фактически мы рассчитали площадь пола или площадь потолка. Для простого прямоугольного помещения они будут равны.
Калькулятор площади помещения
Чтобы выполнить расчет площади помещения используя наш онлайн калькулятор достаточно выполнить всего несколько действий. В соответствующие поля введите сперва ширину помещения, а затем его длину. Не забудьте выбрать единицы измерения (метры, сантиметры или миллиметры).
Когда вы ввели все исходные данные нажмите на кнопку расчет и сразу же получите результаты расчета. Итоговая площадь может быть в выбранных вами единицах измерения (м2, см2 или мм2). Точность калькулятора площади составляет два знака после запятой.
Вот так легко и быстро рассчитает площадь помещения наш калькулятор. К тому же он бесплатный и простой, так что можете пользоваться.
В строительстве бывает так что ещё необходимо знать и площадь всех стен комнаты. Для этого есть калькулятор стен онлайн.
Было полезно? Поделитесь с друзьями!
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Кому-то, наверное, покажется смешным столь «детский» вопрос – «как рассчитать площадь комнаты». Но давайте согласимся с тем, что, во-первых, многие из нас школу заканчивали уже очень давно. Во-вторых, далеко не все в повседневной жизни постоянно сталкиваются с необходимостью проведения геометрических расчетов, и кое-что уже могло позабыться. И, в-третьих, комнаты и стены далеко не всегда и не везде имеют прямоугольную форму, площадь которой вычислить легко и просто. Значит, иногда придется проявить сообразительность и применить более сложные методы расчёта.
А для чего вообще необходимо уметь определять площадь пола, стен, потолка комнаты?
- Эти данные необходимы для планирования проведения ремонта в квартире – можно рассчитать количество потребных строительных материалов.
- Если работу выполняют наемные мастера, то они чаще всего требуют оплату с квадратного метра. Чтобы не стать жертвой обмана, иметь возможность проконтролировать добросовестность работников и не платить лишнего, необходимо уметь правильно определять объемы выполненной работы.
- Умение считать строительные схемы и определять площадь может понадобиться при просмотре вариантов жилых помещений, представляемых на продажу или сдачу в аренду. Кстати, и сумма оплаты некоторых коммунальных услуг также зависит именно от размера полезной и общей площади.
- Правильный подбор осветительных приборов напрямую зависит от площади помещения – на этот счет существуют специальные нормативы освещенности.
- Зная площадь, несложно вычислить и объем помещения. А это – главный параметр при подборе отопительных приборов, климатического оборудования, вентиляционных систем.
Одним словом, такое умение никогда не будет лишним. И если читатель зашел на эту страницу, значит ему понадобилось узнать или освежить в памяти алгоритмы расчета площади. Поэтому, начинаем рассматривать, по принципу «от простого – к сложному».
Подготовка к расчетам
Этот этап, по сути, включает в себя два основных момента. Требуется подготовить место выполнения измерительных работ, необходимые для этого инструмент и принадлежности, и собственно, провести промеры, перенеся результаты на схему или чертеж.
- В идеале, лучше всего проводить все измерения в полностью освобождённой от мебели и иных предметов комнате. При проведении ремонта это обычно так и бывает. Но если замеры проводят для иных целей, то выносить все из помещения, конечно, никто не возьмётся.
Измерения длин сторон комнаты обычно проводят вдоль стенок. Поэтому, необходимо постараться освободить эти участки, так, чтобы можно было полностью, от стены до стены, растянуть ленту рулетки.
- Проверку прямоугольности помещения проще всего выполнить промером диагоналей. Поэтому, может понадобиться пространство и в центре комнаты. Или же должна быть предусмотрена возможность передвижения предметов, которые могут стать помехой для измерений.
Наверняка последуют ироничные замечания – неужели автор, давая такие советы, не слышал никогда о современных электронных лазерных рулетках? Конечно, эти современные приборы помогают не только быстро и качественно произвести замеры линейных и угловых величин – многие из них имеют встроенные функции проведения необходимых расчетов.
Однако давайте «опустимся на землю» — такой инструмент есть пока что не у многих. Профессионалам, да, без него обойтись в настоящее время сложно. Однако в бытовых условиях большинство людей полагаются пока на традиционные способы измерения. Кстати, для проведения замеров лазерной рулеткой свободное пространство так или иначе все равно создавать придется – для беспрепятственного прохождения луча.
- Итак, исходим из того, что замеры проводим обычной рулеткой. Кроме того, помимо блокнота для записей, могут понадобится:
— длинная линейка для отбивки прямых линий (например, может подойти правило или длинный строительный уровень);
— максимально большой (чем больше – тем лучше) строительный угольник;
— импровизированный циркуль – это может быть кусок прочного шнура, привязанный к какому-нибудь острому штырю, который будет играть роль центра;
— чтобы измерить угол – нужен или специальный инструмент, или проведение расчетов с использованием тригонометрических функций. Однако, в тех методиках, которые будут предложены, измерение угла вовсе не станет обязательной процедурой – обойдемся линейными величинами.
— возможно, на полу нужно будет проводить какую-то вспомогательную разметку. Чтобы не пачкать пол мелом или маркером, можно использовать тонкий малярный скотч.
- Все измерения лучше проводить дважды – так будет меньше вероятность допустить какую-либо досадную ошибку по невнимательности.
- Лента рулетки при проведении замеров не должна провисать, на измеряемом участке должна представлять собой прямой отрезок, в натяжку.
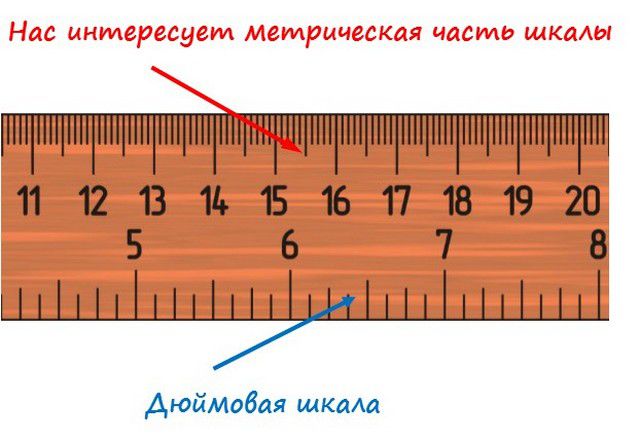
- Внимание на шкалу! Не спутайте систему метрическую и «дюйм – фут», так как на многих измерительных инструментах нанесены обе шкалы.
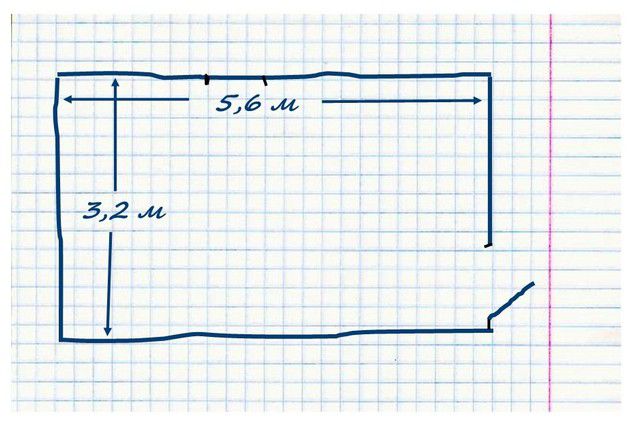
- Работать будет намного проще, если заранее набросать примерный план помещения на бумаге. Вовсе не обязательно его вычерчивать в данном случае супер-аккуратно, в масштабе, с соблюдением требований чертежных стандартов.
Просто намного удобнее станет сразу переносить результаты измерений на бумагу, для проведения дальнейших расчетов.
При замере расстояний нужно будет их записывать в метрах, с округлением до сантиметра, например, 0,82 м или 5,38 м. Тогда и все результаты сразу будут получаться в искомых квадратных метрах.
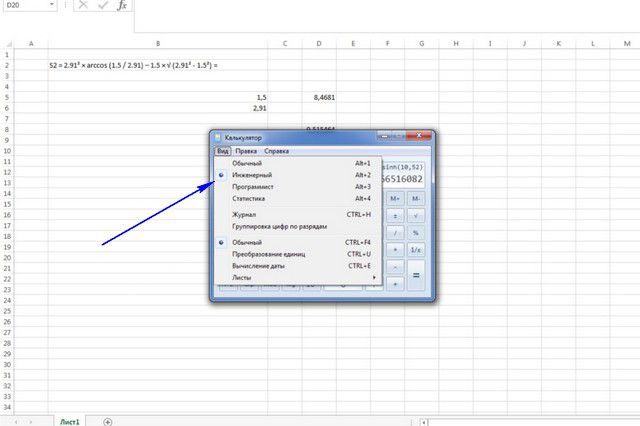
- Некоторые формулы расчета – достаточно громоздкие, содержат тригонометрические функции или вычисления квадратных корней, то есть «в столбик» подсчитать не получится. Отлично, если есть умение проводить расчеты в Excel – все наглядно, плюс весь процесс можно сохранить в файле. Если нет – значит пускается в ход калькулятор. Удобно пользоваться тем, что встроен в Windows – только не забудьте перевести его из «обычного» в «инженерный» через меню «Вид» или же одновременным нажатием клавиш «Alt + 2».
Теперь переходим к рассмотрению возможных вариантов конфигурации комнаты.
Определяем площадь пола комнаты
Прямоугольник
1. Наверное, самая распространенная конфигурация комнаты, особенно в городских многоэтажных застройках. И, соответственно, самый незамысловатый способ расчета площади.
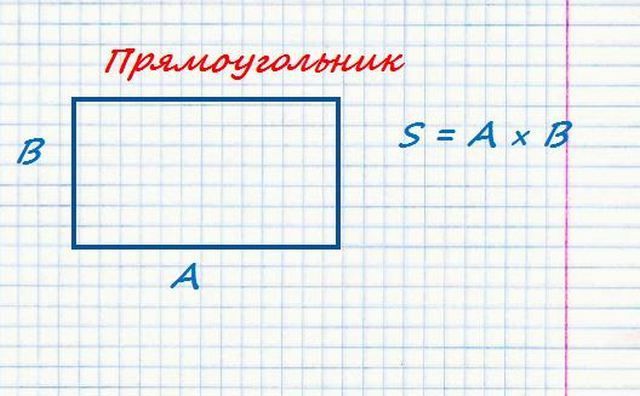
Стороны прямоугольника можно обозначить, как А и В. Таким образом, площадь будет равна:
S = А × В
Противоположные стороны прямоугольника равны между собой, попарно, то есть, по сути, измерить можно только два значения.
Но при этом нельзя забывать о проверке – а прямоугольник ли это? Можно приложить в каждом из углов строительный угольник, но не всегда это дает четкую картину. Проще будет сделать промеры диагоналей и сравнить результаты. Если они совпадают или разница совсем небольшая, то можно считать, что это действительно прямоугольник.
В предлагаемом примере площадь комнаты равна:
S = А × В = 5,82 × 3,77 = 21,94 м²
2. Комната может иметь выступы, ниши, проходы и т.п. прямоугольной формы. Ничего страшного – можно на схеме разбить общую площадь на несколько прямоугольников. Понятно, что после вычислений площадей по участкам все значения суммируются.
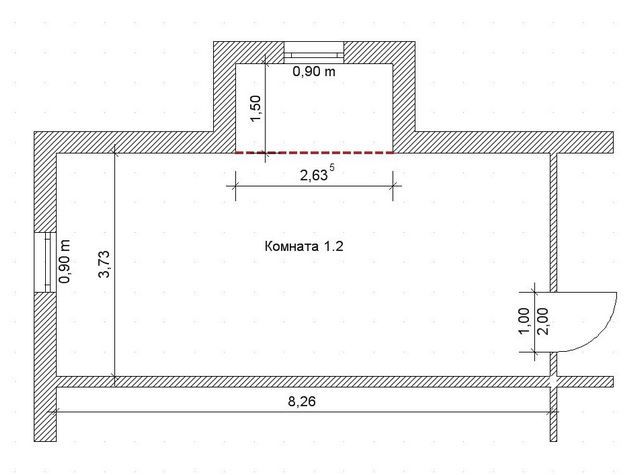
На схеме показан пример обширного помещения с выступающим участком. На схеме красным пунктиром показано разделение комнаты на два прямоугольных участка. Осталось лишь найти площадь каждого и суммировать ее:
Σs = S1 + S2 = 8.26 × 3.73 + 2.63 × 1.50 = 30.81 + 3.95 = 34.75 м²
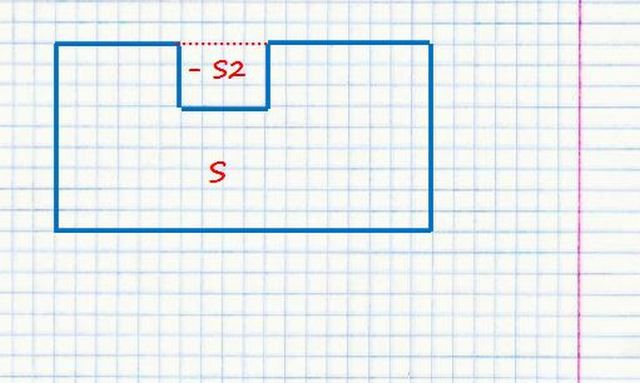
3. Иногда случается так, что выступ наоборот, направлен в сторону помещения и оттого «съедает» часть площади.
Тогда при расчетах можно пойти иным путем – найти площадь этого «украденного» пространства и вычесть ее из площади большого прямоугольника.
Трапеция
Такая ситуация нередко случается в угловых помещениях.
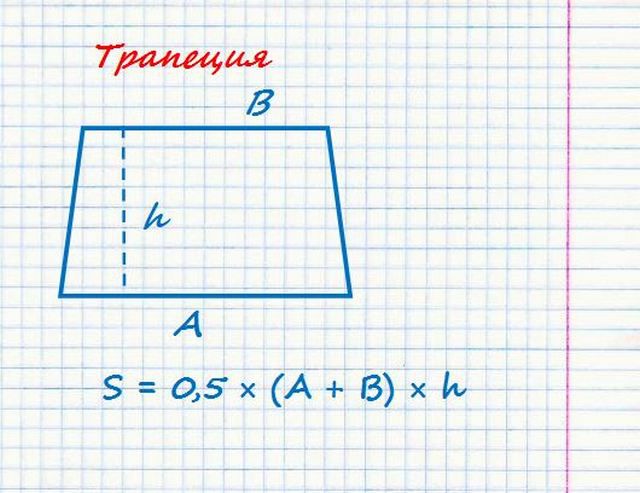
Характерная особенность четырехугольника, именуемого трапецией – две стороны его параллельны друг другу, а другие две могут быть расположены под произвольным углом.
В данном случае чтобы определить площадь необходимо знать три параметра – длины двух параллельных сторон и высоту трапеции, то есть расстояние по перпендикуляру между ними.
S = ½ (A + B) × h
Эта формула универсальна – от углов расположения боковых сторон ничего не меняется, и их значение нам знать необязательно. А вот высоту h лучше промерить в нескольких местах — будет уверенность, что две стороны действительно параллельны друг другу.
Рассмотрим пример:
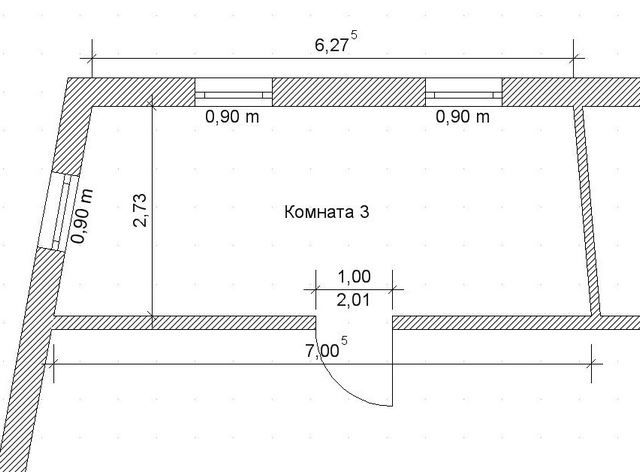
Типичная трапециевидная комната. Делаем замеры и применяем формулу:
S = ½ (A + B) × h = 0,5 × (6,27 + 7,00) × 2,73 = 15,83 м²
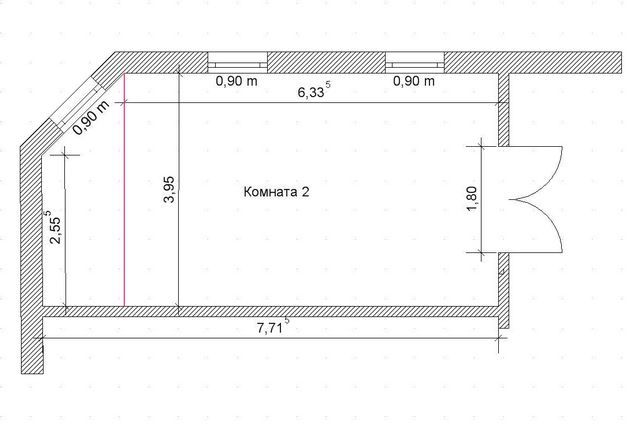
Иногда знание формулы площади трапеции пригодится и при сложных, многоугольных формах помещения. Например, на чертеже снизу показана пятиугольная комната. Ее удобнее всего разделить на два участка – прямоугольник и трапецию (разделены условной красной линией).
Площадь прямоугольника:
S1 = 6.33 × 3.95 = 25 м²
Одна из сторон прямоугольника является и основанием трапеции. А высота трапеции – разница длин противоположных сторон помещения:
h = 7.71 – 6.33 = 1.38 м
Находим площадь трапеции:
S2 = 0.5 × (3.95 + 2.55) × 1.38 = 4,49
Итого, площадь всего помещения равна:
Σs = S1 + S2 = 25.0 + 5.71 = 29,49
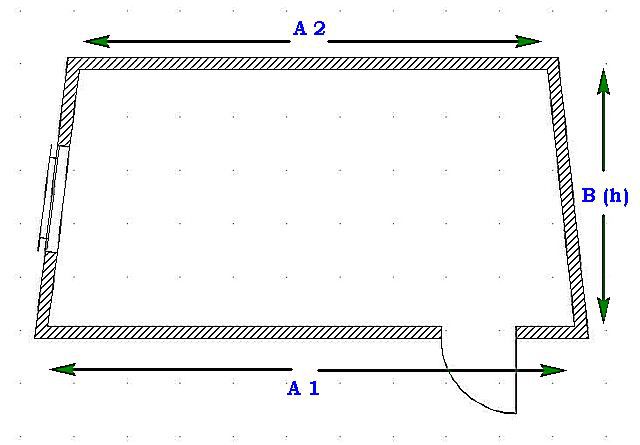
Калькулятор для расчета площади прямоугольных или трапециевидных помещений
Приведенный ниже калькулятор позволяет рассчитывать площади как прямоугольных, так и трапециевидных комнат — единственное отличие, что у прямоугольных значение длин А1 и А2 будет одинаковым.
При необходимости, сразу можно внести поправки на имеющиеся ниши или выступы.
Перейти к расчётам
Треугольники
До сих пор во всех примерах соблюдалась какая-то «правильность» — помещения или прямоугольные, или, по крайней мере, имеют параллельные стены. А что делать, если сложная форма комнаты никак не позволяет ее разбить на такие «правильные» фигуры?
Делать нечего, придется разбивать на треугольники совершенно производной формы, а потом поочередно вычислять их площадь и суммировать.
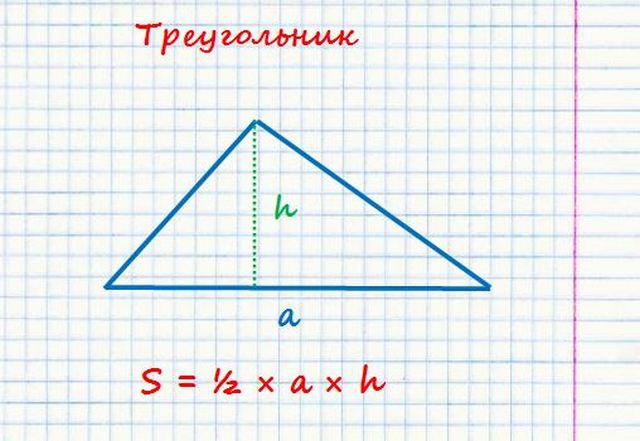
Площадь треугольника вообще-то вычислить несложно – необходимо умножить длину его основания на перпендикулярную этому основанию высоту, проведенную из противоположного угла, и разделить на два.
S = ½ × а × h
Сложность в том, что точно отбить перпендикулярную высоту в условиях замеров на полу, на больших расстояниях, да еще и без специальных инструментов – не так и просто. Запросто можно совершить чисто геометрическую ошибку, которая потянет за собой неправильный результат вычисленной площади.
В этом случае лучше воспользоваться формулой Герона для треугольников. Она, правда, несколько громоздкая, но зато позволяет точно определить площадь исходя исключительно из длин сторон треугольника. Выглядит она таким образом:
S = √ p × (p – a) × (p – b) × (p – c)
где:
— а, b и с – длины сторон треугольника;
— р – половина периметра треугольника, то есть р = ½ (а + b + с)
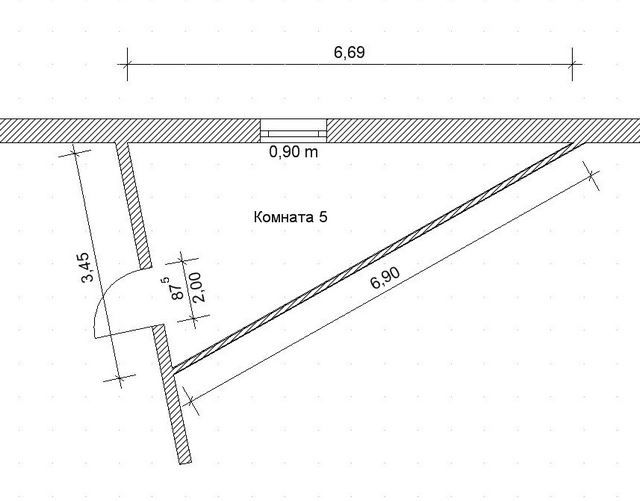
Разбираемся на примере треугольной комнаты (такие тоже бывают иногда — в подсобных помещениях, под лестничными площадками и т.п.).
Итак, величина углов нас абсолютно не интересует – замеряем только длины всех сторон.
а = 6.90 м
b = 3.45 м
c = 6.69 м
p = 0.5 × (6.90 + 3.45 + 6.69) = 8.52
S = √ p × (p – a) × (p – b) × (p – c) =
= √ 8.52 × (8.52 – 6.90) × (8.52 – 3.45) × (8.52 – 6.69) =
= √ 8.52 × 1.62 × 5.07 × 1.83 = √ 128.06 = 11.32 м²
Если знать, как рассчитать площадь произвольного треугольника по его сторонам, то не представит труда определить площадь практически любого помещения с прямолинейными стенками, независимо от расположения сторон. На примере ниже показана четырёхугольная комната абсолютно «неправильной» формы. Разбивать ее на прямоугольники с «довеском» треугольников – нет смысла. Лучше уже сразу по диагонали надвое – получаем два треугольника.
Красным цветом показана диагональ, которая становится общей стороной для обоих треугольников.
Вооружившись формулой Герона, вычисляем обе площади и суммируем их.
р1 = 0.5 × (5.96 + 5.19 + 2.61) = 6.88
S1 = √ 6.88 × (6.88 – 5.96) × (6.88 – 5.19) × (6.88 – 2.61) = √45.67 = 6.76 м²
р2 = 0.5 × (5.96 + 6.63 + 4.34) = 8.47
S2 = √ 8.47 × (8.47 – 5.96) × (8.47 – 6.63) × (8.47 – 4.34) = √ 161.56 = 12.7 м²
Σs = S1 + S2 = 6.76 + 12.7 = 19.46 м²
На первый взгляд, возможно, покажется сложным и громоздким, но на самом деле – все просто. Главное, сделать тщательные промеры и не запутаться в вычислениях.
А чтобы читателю было еще проще, ниже размещен калькулятор, мгновенно рассчитывающий площадь треугольника по длинам трех его сторон. Обратите внимание, что значения длин необходимо вводить в сантиметрах.
Калькулятор расчета площади треугольного помещения
Перейти к расчётам
Криволинейные фигуры
Бывает, что в помещении есть участки, имеющие округлые формы. Значит, нужно рассмотреть варианты, как подойти к вычислениям в этом случае. Кроме того, навыки подобных вычислений будут необходимы для расчета площади стены, на которой есть арочные дверные или оконные проемы.
Слишком сложные криволинейные фигуры, площадь которых можно определить только интегральным исчислением, рассматривать не станем – эти варианты встречаются чрезвычайно редко, и без особых инструментов здесь делать нечего. А вот фигуры, в основе которых лежит окружность, рассчитать вполне возможно. Чаще всего на практике встречаются полукруг, четверть круга или сегмент.
Круг и сектор
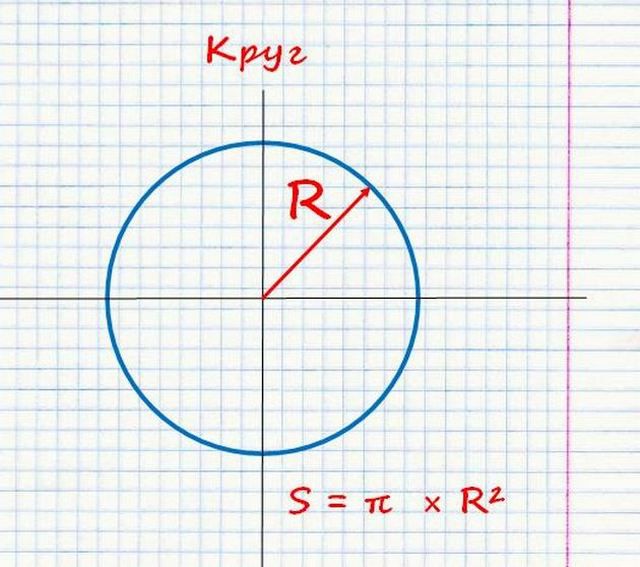
Саму площадь круга найти несложно – нужно знать только его радиус (R).
S = π × R²
Теперь – несколько примеров определения площади с секторными фрагментами круга (половинка и четверть):
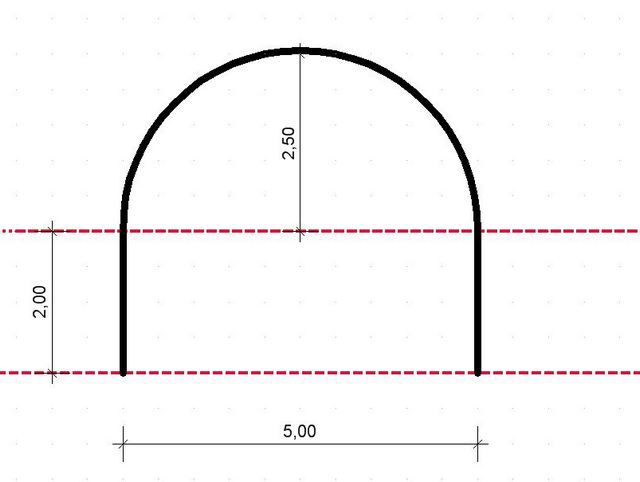
Нужно определить площадь полукруглой залы (или арки на стене). Фигуру можно разбить на две – прямоугольник (S1) и полукруг (S2).
S1 = 5.00 × 2.00 = 10.00 м²
S2 = ½ × 3.14 × 2.50² = 9.8 м²
Σs = 10,00 + 9,8 = 19,8 м²
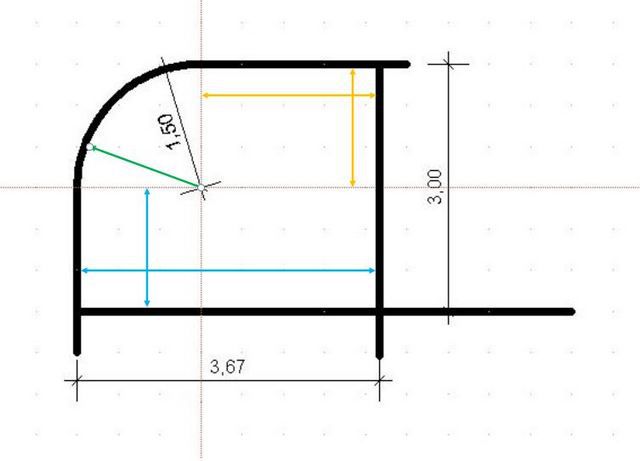
Другой пример, когда дуга соединяет две перпендикулярные стены, образуя, таким образом, четверть круга.
Это помещение можно разбить на три участка: два прямоугольника (их стороны выделены голубыми и желтыми стрелками), и четверть круга с радиусом, выделенным зелёной стрелкой.
Нижний прямоугольник (голубой):
S1 = 3.67 × (3.0 – 1.5) = 5.51 м²
Верхний прямоугольник (желтый):
S2 = (3.67 – 1,5) × 1.5 = 3.25 м²
Четверть круга:
S3 = ¼ × 3.14 × 1.5² = 1.76 м²
Итого общая площадь:
Σs = 5.51 + 3.25 + 1.76 = 10.52 м²
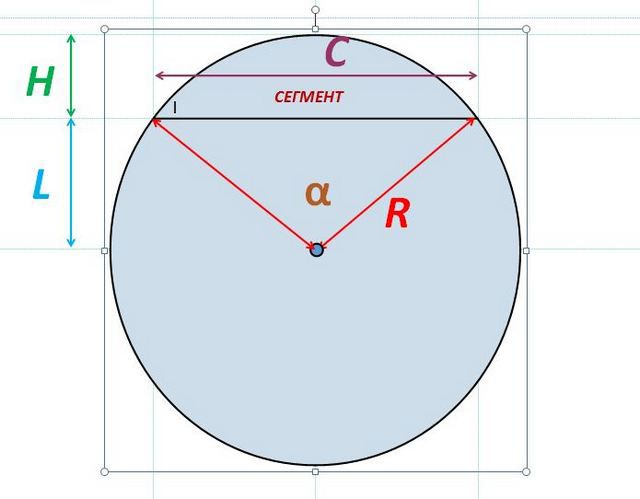
Сегмент
А вот теперь – задачка несколько посложнее. Иногда округлости арок или комнат принимают форму не сектора, а сегмента, то есть части круга, ограниченной дугой и образующей дугу хордой (отрезком, соединяющим две точки на окружности).
Есть специальные формулы, позволяющие определить площадь этой фигуры на основании ее не угловых, а только лишь линейных размеров.
Базовыми величинами будут служить радиус (R) и длина хорды (C) или высота (H).
Формула через длину хорды:
S = R² × arcsin (C/2R) – 0.25 × C × √ (4R² — C²)
А если отталкиваться от высоты сегмента, то сначала можно определить значение L:
L = R — H
А формула принимает такой вид:
S = R² × arccos (L/R) – L × √ (R² — L²)
Разбираемся на примере.
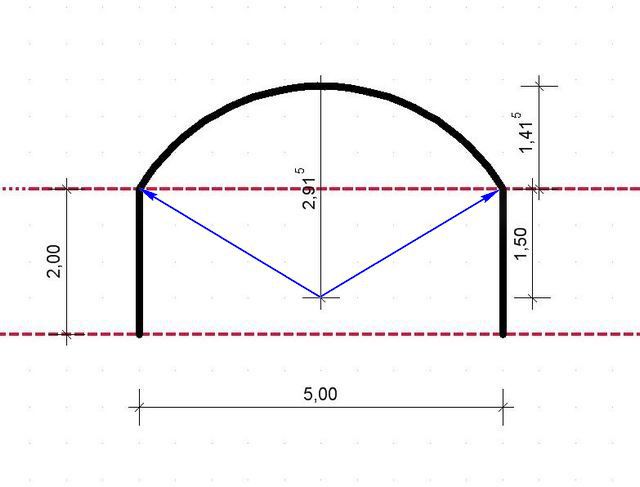
Необходимо вычислить площадь такого помещения:
Перво-наперво, в этом случае необходимо найти центр окружности, чтобы определиться с ее радиусом. Это можно сделать экспериментальным путем, перемещая самодельный циркуль (например, из шнура) по осевой линии, пока не будет обнаружена точка, расстояние от которой и до краев дуги, и до ее центра станет равным. Это расстояние – и есть радиус.
Теперь несложно промерить и все остальные параметры. R = 2.91 м, Н = 1.41 м, L = 1.5 м.
В итоге получаем две фигуры – прямоугольник и сегмент.
Площадь прямоугольника:
S1 = 5.00 × 2.00 = 10.00 м²
Находим площадь сегмента на основании радиуса и длины хорды (в нашем случае длина хорды, вполне очевидно, равна ширине помещения).
S2 = 2.91² × arcsin (5/(2×2.91)) – 0.25 × 5.0 × √ (4 × 2.91² — 5.0²) =
= 5.01м²
(При вычислении на калькуляторе обязательно установите единицу углового измерения – радиан. При подсчёте в Excel радианы установлены по умолчанию).
Просто ради интереса – та же площадь, но через высоту сегмента:
S2 = 2.91² × arccos (1.5 / 2.91) – 1.5 × √ (2.91² — 1.5²) = 4.99 м²
Полученная разница в 0,02 м² – просто результат округлений длинных дробных чисел. Очевидно, что здесь вполне можно принять среднее значение в 5,0 м²
Итого, общая площадь помещения:
Σs = 10.00 + 5.00 = 15.00 м²
Определение площадей стен и потолка
Пол в комнате – не единственная плоскость, площадь которой необходимо знать. Часто для вычисления количества необходимых строительных или отделочных материалов, для определения объемов работ приходится находить площадь стен и потолка.
Законы геометрии одинаковы для всех двухмерных фигур, так что ничего нового их области математики сказано не будет. Есть только некоторые нюансы:
Стены
Казалось бы, чего проще: площадь стены – это ее длина, умноженная на высоту. Стало быть, общую площадь поверхности стен в комнате можно найти произведением периметра помещения на высоту.
Да, это справедливо, но только лишь для комнат, у которых высота потолка у стен одинакова в любой точке. А, например, в мансардных помещениях стена может быть трапециевидной или даже треугольной. Поэтому, на это стоит обратить внимание. Как найти площадь треугольника или трапеции – повторять не будем.
Далее – из общей площади стены необходимо вычесть оконные или дверные проемы. Ничего сложного – делаются замеры по внешней поверхности коробок и рам, и производится соответствующий расчет, в зависимости от геометрической фигуры.
Кстати, если площадь стен вычисляется для того, чтобы определить количество стандартных рулонов обоев для проведения ремонта, то можно предложить вниманию табличку, которая сразу подскажет это число, исходя из периметра комнаты и высоты потолка:
Количество стандартных рулонов обоев 10,5 × 0,52 м (в периметр помещения включены все дверные и оконные проёмы).
| Высота потолка (м) | Периметр комнаты (м) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 10 | 12 | 13 | 14 | 15 | 16 | 17 | 19 | 20 | 21 | 22 | 23 | 25 | 26 | 27 | 28 | 30 | |
| 2,15 ÷ 2,30 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 10 | 10 | 11 | 12 | 12 | 13 | 13 |
| 2,30 ÷ 2,45 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 10 | 10 | 11 | 11 | 12 | 13 | 13 | 14 |
| 2,45 ÷ 2,60 | 5 | 5 | 6 | 7 | 7 | 8 | 9 | 9 | 10 | 10 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 15 |
| 2,60 ÷ 2,75 | 5 | 5 | 6 | 7 | 7 | 8 | 9 | 9 | 10 | 10 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 15 |
| 2,75 ÷ 2,90 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 10 | 10 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 15 | 16 |
| 2,90 ÷ 3,05 | 6 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 16 | 16 | 17 |
| 3,05 ÷ 3,20 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 | 15 | 16 | 16 | 17 | 18 | 19 |
Потолок
В подавляющем числе случае с потолком вообще проблем возникать не должно. Если он горизонтальный, то это точная проекция пола, площадь которого уже определена.
Чердачные, мансардные помещения могут быть исключениями, так как плоскость потолка там бывает под углом к полу, а иногда — даже ломаная, состоящая из нескольких поверхностей, пересекающихся между собой.
Ничего страшного. Не нужно углубляться в тригонометрию и вычислять углы между полом, стенами и потолком. Просто надо «виртуально» разбить такие сложные поверхности на несколько плоских фигур, промерить их линейные величины. А все остальное мы уже умеем – формулы расчета будут точно такими же.
И, наконец, в завершение статьи – видео, рассказывающее о том, каким помощником может стать лазерный дальномер (рулетка).