Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).
5 способов вычисления:
- через три стороны трапеции;
- умножив высоту трапеции на среднюю линию;
- через основание и углы;
- через диагонали и углы между ними;
- через четыре стороны.
Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.
Площадь прямоугольной трапеции по трём сторонам
Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.
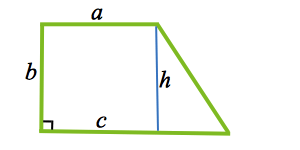
a – малое основание;
b – перпендикулярная сторона;
c – большое основание;
h – высота.
Рисунок 1. Прямоугольная трапеция. Высота h.
[boldsymbol{S}=frac{mathbf{1}}{mathbf{2}} *(boldsymbol{a}+boldsymbol{c}) * boldsymbol{b}, text { где } mathbf{S}], где S – площадь прямоугольной трапеции.
Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.
Задача.
Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.
Решение:
Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.
[boldsymbol{S}=frac{1}{2} *(4,84+7,88) * 4,64=mathbf{2 9}, mathbf{5 1} text { кв.см }]
Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.
Площадь прямоугольной трапеции по высоте и средней линии
Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.
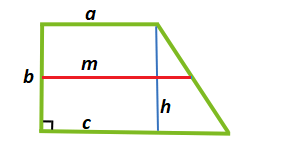
[boldsymbol{S}=boldsymbol{m} * boldsymbol{h}], где S – площадь фигуры, m – средняя линия, а h – высота, которую можно заменять на перпендикулярную основаниям сторонуb.
Задача.
Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.
Решение:
Найдём площадь трапеции путём умножения известных величин.
[boldsymbol{S}=4,64 * 6,36=29,51 text { кв.см }]
Ответ: S = 29,51 кв.см.
Вычисление площади по основаниям и углам
Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.
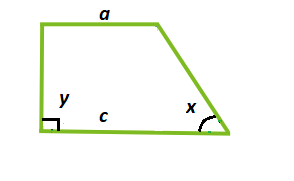
[S=frac{1}{2} *left(c^{2}-a^{2}right) * frac{sin (y) * sin (x)}{sin (y+x)}], где S – площадь; с – большое основание;a – малое основание;
y, x – первый и второй угол при основании.
Задача.
Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8о?
Решение:
Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.
[boldsymbol{S}=frac{1}{2} *left(7,88^{2}-4,84^{2}right) * frac{sin (90) * sin (56,8)}{sin (90+56,8)}=mathbf{2 9 , 4 8} mathbf{кв.см}]
Ответ: S = 29.48 кв.см.
Нет времени решать самому?
Наши эксперты помогут!
Площадь прямоугольной трапеции через диагонали и углы между ними
Умножив синус угла, образованный на пересечении диагоналей, на произведение диагоналей, делённое пополам, получим площадь прямоугольной трапеции.
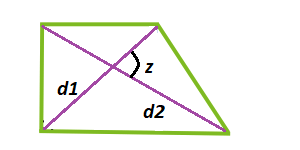
[S=frac{1}{2} * d 1 * d 2 * sin (x)], где S – площадь; d1 – диагональ 1; d2 – диагональ 2; z – угол между диагоналями.
Задача.
Найдите площадь прямоугольной трапеции, имя данные первой диагонали d1, второй – d2 и угла между ними z. d1 = 2,23 см; d2 = 2,65 см, z = 57o.
Решение:
Пользуясь формулой расчёта площади, при известных диагоналях и углу между ними, составим решение.
[boldsymbol{S}=frac{1}{2} * 2,23 * 2,65 * sin (57)=mathbf{2}, mathbf{4 8} mathbf { кв.см }]
Ответ: S=2,48 кв.см
Площадь прямоугольной трапеции, исходя из значения всех её сторон
Если известны показатели всех сторон прямоугольной трапеции, то вычислить её площадь можно по формуле, приведённой ниже.
[left.S=frac{a+c}{2} * sqrt{e^{2}-left(frac{(c-a)^{2}+e^{2}-b^{2}}{2 *(c-a)}right.}right)^{2}], где a – малое основание; c – большое основание; b – перпендикулярная основаниям сторона; e – неперпендикулярная боковая сторона.
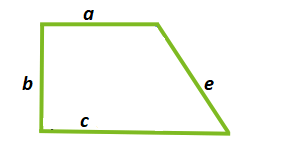
Задача.
Дано: a = 3 см; b = 3 см; c = 5 см; e = 3,5 см.
Найти: площадь трапеции S.
Решение: применяя формулу расчёта площади по всем сторонам фигуры, найдём площадь трапеции.
[S=frac{3+5}{2} * sqrt{3,5^{2}-left(frac{(5-3)^{2}+3,5^{2}-3^{2}}{2 *(5-3)}right)^{2}}=11,98 mathbf { кв.см} .]
Ответ: S = 11,98 кв.см.
Площадь прямоугольной трапеции: онлайн калькулятор, формула расчета, пример вычисления
Сергей Феликсович Савельев
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Определение 1
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции

Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = frac12 cdot (a + c) cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.
Пример 1
Задача
Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2.42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
Решение:
Воспользуемся приведённой выше формулой:
$S =frac{(2.42 + 3.93) cdot 2.32}{2} = 7.37$ кв. см.
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:
$S = m cdot h$, где
$S$ – площадь трапеции,
$m$ – средняя линия,
$h$ – высота трапеции.
Другой способ расчёта площади прямоугольной трапеции — через длины оснований и два угла, расположенных при одном основании.
Площадь трапеции через ее основание и углы

Формула нахождения площади трапеции через ее основание и углы при основании:
$S = frac12 cdot (b^2 – g^2) cdot frac{sin (α) cdot sin (γ)}{sin (α + γ)}$, где
$S$ – площадь трапеции,
$b$ – большее основание,
$g$ – малое основание,
$α$ – первый угол при основании,
$γ$ – второй угол при основании.
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =frac12 cdot d1 cdot d2 cdot sin (α)$, где
$S$ – площадь трапеции,
$d1$ – первая диагональ,
$d2$ – вторая диагональ,
$α$ – угол между диагоналями.
Рассмотрим пример.
Пример 2
Задача
Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2.22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
Решение:
Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:
$S = frac{2.22 cdot 2.64 cdot 0.83}{2} = 2.43$ кв. см.
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное.
И наконец, рассмотрим случай когда нет данных о том, какие стороны являются основаниями, а какая сторона расположена под прямым углом, но при этом известны все стороны трапеции.
Площадь трапеции по четырём сторонам

Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
$S = frac{a + b}{2} cdot sqrt{c^2 – (frac{(b – a)^2 + c^2 – d^2}{2 cdot (b – a)})^2}$, где
$S$ – площадь трапеции,
$a$ – малое основание,
$b$ – большее основание,
$c, d$ – боковые стороны.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 26.06.2019
Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.
I. Площадь трапеции равна произведению полусуммы оснований на высоту.
 Площадь прямоугольной трапеции ABCD,
Площадь прямоугольной трапеции ABCD,
AD∥BC,
![]()
равна
![]()
Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть
![]()
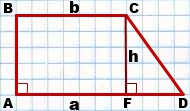
Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):
![]()
II. Площадь трапеции равна произведению средней линии на высоту.
 Если MN — средняя линия прямоугольной трапеции ABCD,
Если MN — средняя линия прямоугольной трапеции ABCD,
![]()
то площадь
![]()
Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:
![]()
III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.
 Для прямоугольной
Для прямоугольной
трапеции
ABCD,
AD∥BC,
![]()
Так как sin(180º-α)=sin α, то также
![]()
Если AC=d1, BD=d2, ∠COD=φ, то
![]()
 В частности, если диагонали трапеции перпендикулярны, то
В частности, если диагонали трапеции перпендикулярны, то
![]()
VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

![]()
Так как в трапецию можно вписать окружность, то
AD+BC=AB+CD=p. Следовательно,
![]()
или
![]()
Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:
![]()
![]()
Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула
![]()
Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.
![]()
или
![]()
Особенности и свойства трапеций
Прежде чем разобраться, как найти площадь прямоугольной трапеции, следует подробнее рассмотреть свойства этого класса фигур. Все они представляют собой выпуклые четырехугольники, у которых две и всего две стороны параллельны между собой. Они называются основаниями и имеют разную длину. Оставшиеся две стороны наклонены друг относительно друга под определенным и неравным нулю углом. Они называются боковыми.
Нетрудно догадаться, что основания фигуры должны всегда отличаться по длине. В противном случае параллельными между собой окажутся также боковые стороны, и получится не трапеция, а прямоугольник или квадрат.
Терминология и элементы
Из определения трапеции следует, что эта фигура состоит из двух оснований и двух боковых сторон. Помимо них, в геометрии выделяют также следующие линейные характеристики:
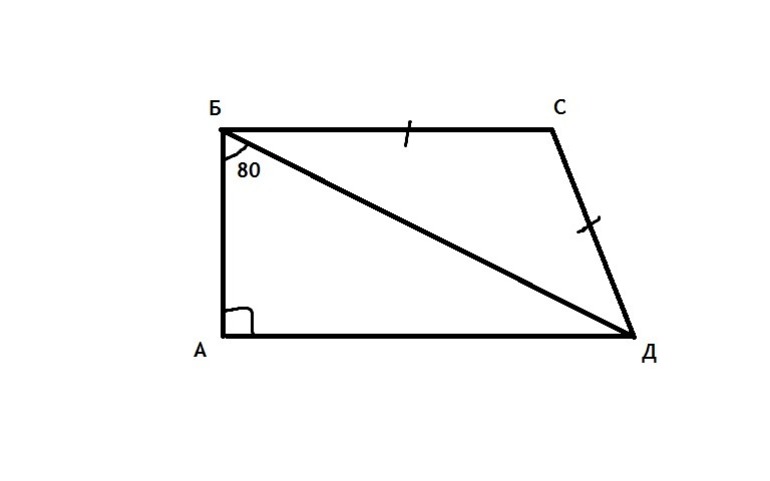

- Диагонали — соединяющие несмежные (противоположные) вершины отрезки, в общем случае они имеют разную длину и могут быть вычислены из знания всех длин сторон фигуры. Соответствующие формулы имеют вид: D1 = (a*b + d 2 — a*(d 2 -c 2 )/(a-b))^0,5 и D2 = (a*b + c 2 — a*(c 2 -d 2 )/(a-b))^0,5. Здесь буквами a и b обозначены основания, c и d — это боковые стороны.
- Высота — расстояние между параллельными основаниями, она соответствует длине перпендикуляра, опущенного от малого основания к большому. Обычно ее обозначают буквой h. Через четыре стороны фигуры она так же, как и диагонали, может быть рассчитана. Соответствующая формула является несколько громоздкой. Она имеет вид: h = (4*(a-b)^2*d 2 — (d 2 + (a-b)^2 — c 2 )^2)^0,5/(2*(a-b)).
- Средняя линия или медиана M — отрезок, который соединяет середины сторон боковых, его длина однозначно рассчитывается из знания длин обоих оснований. Выражение для M имеет следующую форму: M = (a+b)/2 — полусумма длин оснований.
- В некоторых задачах также встречается отрезок n, который соединяет середины обеих диагоналей. Его длина рассчитывается как полуразница оснований: n = (a-b)/2.
Все формулы для нахождения длин соответствующих линейных элементов трапеции справедливы независимо от значений ее сторон и внутренних углов.
Существующие типы
Несмотря на простоту построения трапеции, она бывает нескольких типов. Последние определяются однозначно с учетом значения внутренних углов фигуры. В геометрии выделяют следующие типы:

- Общий. Этот тип фигуры является наименее симметричным. В ней все четыре угла отличаются друг от друга, при этом два из них являются тупыми, и два острыми. Их расположение может быть либо попарным, либо противоположным. Кроме того, трапеция общего типа имеет разные длины боковых сторон.
- Равнобедренный. Это самый симметричный тип фигуры. Равнобедренная трапеция по определению имеет две одинаковые по длине боковые стороны и, как следствие, равные попарно углы при основаниях (два острых и два тупых). Прямая, проходящая через середины оснований, является осью симметрии фигуры. Ее диагонали равны, а противоположные углы в сумме составляют 180 °. В такую трапецию можно вписать окружность, радиус которой составит половину высоты фигуры (r = h/2), однако, это не всегда возможно.
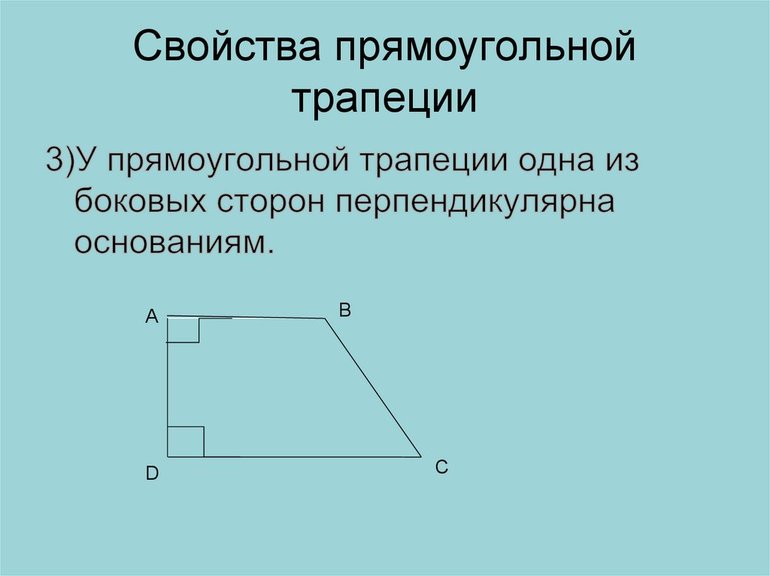
- Прямоугольный. Как следует из названия, для этого типа трапеции характерно наличие внутренних прямых углов, то есть таких, мера которых составляет 90 °. Поскольку сумма односторонних углов, заключенных между параллельными прямыми, всегда составляет 180 °, то в прямоугольной трапеции всегда существует два прямых угла. Два других угла являются острым и тупым.
Для всех перечисленных типов трапеции справедлив тот факт, что сумма четырех углов составляет 360 °. В любой тип фигуры можно вписать окружность. Для этого необходимо, чтобы выполнялось следующее условие:
a + b = c + d.
Другими словами, сумма длин оснований должна быть в точности равна сумме боковых сторон.
Прямоугольная фигура и ее характеристики
Несмотря на невысокую симметрию трапеции с прямыми углами, работать с ней удобно при решении задач, поскольку можно напрямую использовать теорему Пифагора.
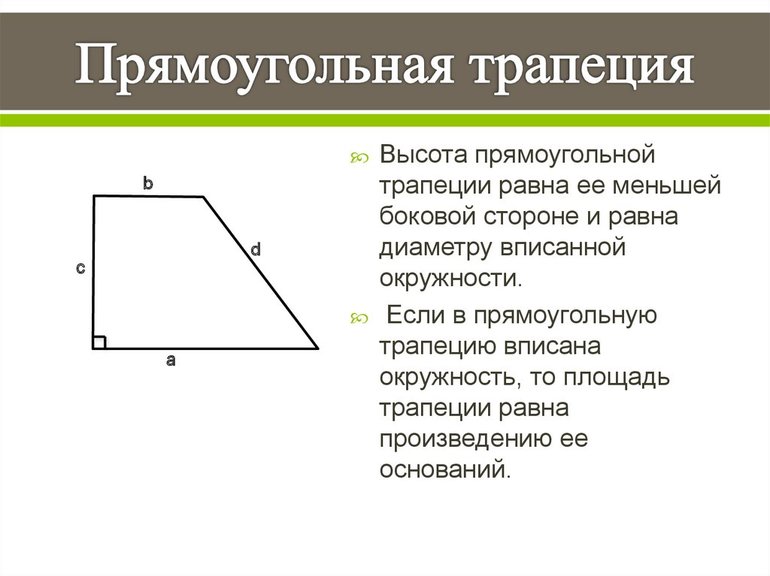
Пусть имеется фигура, в которой a и b — это основания, c — сторона, которая им обоим перпендикулярна и образует с ними прямые внутренние углы, d — боковая сторона, которая наклонена под некоторым углом к основаниям. Из такого построения ясно, что боковая сторона c также является высотой h фигуры.
Углы и диагонали
Формулы для расчета внутренних углов и длин диагоналей в прямоугольной фигуре имеют простой вид. Чтобы найти тупой и острый углы, достаточно рассмотреть прямоугольный треугольник, который образован следующими отрезками:
- перпендикуляром к основанию c;
- боковой стороной d;
- стороной a-b.
Нетрудно доказать, что синус острого угла α при основании может быть рассчитан по следующей формуле:
sin (α) = c/d.
Поскольку вместе с тупым углом β он составляет 180 °, тогда справедливы равенства:
sin (α) = sin (β) = c/d и β = 180 ° – α.
Для вычисления диагоналей прямоугольной трапеции можно воспользоваться общими формулами для D1 и D2.
Однако, для этого типа фигуры их можно упростить, воспользовавшись теоремой Пифагора. Любая из проведенных диагоналей образует внутри рассматриваемой трапеции прямоугольный треугольник, поэтому для D1 и D2 можно записать следующие равенства:
- D1 = (a 2 + c 2 )^0,5;
- D2 = (b 2 + c 2 )^0,5.
Для вычисления диагоналей D1 и D2 необязательно знать длину боковой стороны d.
Вычисление площади
Существует несколько выражений, используя которые можно определить площадь любой трапеции. Для прямоугольной фигуры все эти формулы имеют упрощенный вид. В первую очередь следует отметить общее выражение для площади S, которая равна произведению медианы M на высоту h:
S = M*h.
Для прямоугольной трапеции эта формула преобразуется в следующее равенство:
S = c*(a+b)/2.
Где h=c и M = (a+b)/2.
Удобно определять площадь рассматриваемой фигуры также через ее диагонали D1, D2 и угол их пересечения γ. Эта формула имеет вид:
S = D1*D2/2*sin (γ).
То есть половина произведения диагоналей на синус угла их пересечения дадут площадь всей фигуры. Необходимо отметить, что неважно, какой брать угол (острый или тупой) они связаны друг с другом (в сумме дают 180 °) и их синусы равны. Если диагонали пересекаются под прямым углом, то формула для S сводится к выражению:
S = D1*D2/2.
Существует еще одна формула площади трапеции прямоугольной через ее основания a, b и острый угол α. Применяя следующие рассуждения и выкладки можно ее получить:

- Следует рассмотреть прямоугольный треугольник, ограниченный отрезками c, b-a и d, где основание b больше, чем a.
- Высота c определяется следующей тригонометрической формулой: c = (b-a)*tg (α).
- Площадь фигуры рассчитывается из выражения общего типа: S = (b+a)*(b-a)*tg (α)/2. Эту формулу можно преобразовать таким образом: S = (b 2 — a 2 )*tg (α)/2.
Аналогичную формулу можно использовать, если известен не острый угол α, а тупой β. В этом случае выражение для S примет вид:
S = (a 2 -b 2 )*tg (β)/2.
Функция tg (β) здесь является отрицательной величиной, поэтому вычитаемое и уменьшаемое в множителе a-b поменялись местами. Все выражения для расчета площади применимы при определении объема призм в трехмерном пространстве, у которых основания представляют собой трапеции.
Примеры решения задач
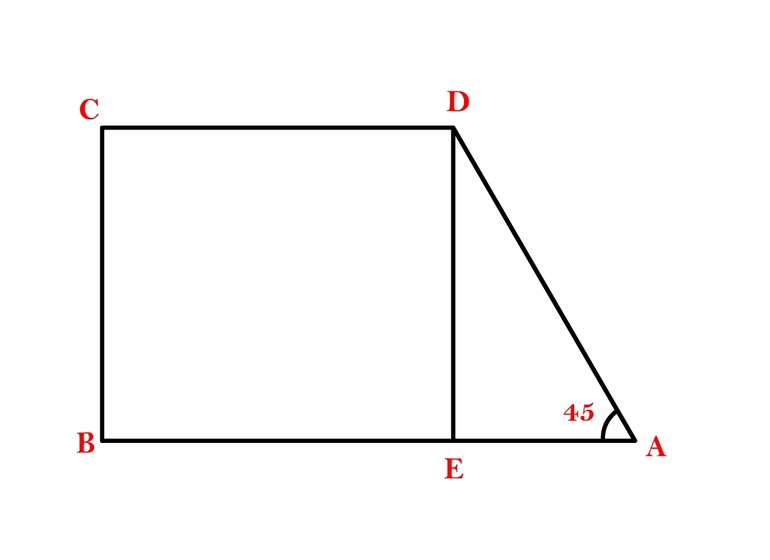
Пример 1. Пусть задана прямоугольная трапеция, медиана которой равна 12 см и острый угол при основании составляет 45 °. Также известно, что боковая сторона, которая не является высотой, составляет 10 см. Необходимо рассчитать площадь этой фигуры.
Если рассмотреть треугольник прямоугольный, который образован двумя боковыми сторонами и заданным острым углом, то можно рассчитать высоту фигуры:
h = d*sin (α) = 10*sin (45 °) = 7,071 см.
Поскольку из условия задачи известна медиана, то можно применить общую формулу для определения площади трапеции:
S = h*M = 7,071*12 = 84,852 см 2 .
Любопытно отметить, что для решения этой задачи не понадобилось знать длины каждого из оснований.
Пример 2. Известно, что большее из оснований трапеции прямоугольной имеет длину 12 см, ее наклонная сторона равна 10 см, а угол при основании составляет 53,13 °. Необходимо выяснить, как найти площадь прямоугольной трапеции из этих данных.
Для решения задачи удобно использовать следующие общепринятые обозначения:
- α = 53,13 °;
- b = 12 см;
- d = 10 см.
Рассматривая треугольник с прямым углом, который заключен между сторонами b-a, d и c, можно вычислить все неизвестные длины отрезков:
- c = d*sin (α);
- b-a = d*cos (α), откуда a = b — d*cos (α).
Общая формула для площади трапеции приобретает вид:
S = M*h = (a+b)/2*c = (2*b — d*cos (α))*d*sin (α)/2.
Все величины в формуле известны из условия задачи. Если их подставить, то получится ответ: 72 см2.
Пример 3. Известно, что в трапеции с прямыми углами диагонали составляют 7 см и 11 см, высота фигуры равна 5 см. Необходимо найти ее площадь.

Из теоремы Пифагора следует, что каждое из оснований трапеции может быть вычислено следующим образом:
- a = (D1 2 -c 2 )^0,5 = (49−25)^0,5 = 4,9 см;
- b = (D2 2 -c 2 )^0,5 = (121−25)^0,5 = 9,8 см.
Тогда площадь фигуры составит: S = (a+b)*c/2 = (4,9+9,8)*5/2 = 36,75 см2.
Таким образом, прямоугольная трапеция является простой фигурой, для вычисления площади которой удобно воспользоваться теоремой Пифагора. Существуют несколько формул для определения величины S, параметрами которых являются длины сторон и непрямые углы.
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым


