3 октября 2013
Сегодня мы разберем самый простой прием, который используется в задаче B5 ЕГЭ по математике для нахождения площадей фигур, начерченных на координатной сетке. Этот метод также известен как метод описанного прямоугольника.
Рассмотрим самый простой случай:
- Фигура наложена на координатную сетку;
- Все вершины фигуры лежат в узлах этой сетки;
- Все внутренние углы фигуры меньше 180 °. Т.е. фигура является выпуклой.
Для работы нам потребуются две формулы:
- Sтр = 0,5ab — площадь прямоугольного треугольника с катетами a и b.
- Sпр = ab — площадь произвольного прямоугольника со смежными сторонами a и b.
Итак, задача B5 из реального ЕГЭ по математике:
Задача B5. Найдите площадь пятиугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратным сантиметрах.

В первую очередь строим описанный прямоугольник, причем так, чтобы на каждой из его сторон находилась хотя бы одна из сторон исходной фигуры.
В нашем случае оказалось, что три вершины исходной фигуры действительно лежат на сторонах описанного прямоугольника. А вот две оставшиеся лежат внутри красного периметра, поэтому для них требуется дополнительное построение. Проведем из каждой вершины высоты к ближайшим сторонам:

Готово! Мы получили прямоугольник, внутри которого заключена наша фигура, а также 7 маленьких фигур, чьи площади считаются по формулам прямоугольного треугольника и прямоугольника. Эти дополнительные фигуры называются разбиением.
Давайте обозначим площади этих фигур: S1, S2, S3, S4, S5, S6 и S7. Получим следующую картинку:
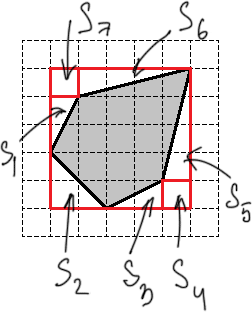
Теперь считаем каждую из обозначенных площадей. Имеем:
S1 = 0,5 · 1 · 2 = 1;
S2 = 0,5 · 2 · 2 = 2;
S3 = 0,5 · 1 · 2 = 1;
S4 = 1 · 1 = 1;
S5 = 0,5 · 4 · 1 = 2;
S6 = 0,5 · 1 · 4 = 2;
S7 = 1 · 1 = 1.
Далее считаем общую площадь красного прямоугольника. На самом деле это квадрат, каждая сторона которого равна 5. Итого площадь равна:
S0 = 5 · 5 = 25
Теперь осталось найти площадь закрашенной фигуры — ту самую, которую от нас и просят найти в задаче B5 ЕГЭ по математике. Для этого из общей площади S0 надо вычесть площади тех кусочков S1, S2, …, S7, которые мы только что считали. Получим:
S = S0 − (S1 + S2 + … + S7) = 25 − (1 + 2 + … + 1) = 25 − 10 = 15
Вот и все решение! Площадь закрашенной фигуры равна 15. Надеюсь, этот урок будет полезен тем, кто начинает готовиться к ЕГЭ по математике.
Смотрите также:
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)

- Площади многоугольников на координатной сетке

- Как сдать ЕГЭ по математике

- Сводный тест по задачам B12 (1 вариант)

- Однородные тригонометрические уравнения: общая схема решения

- ЕГЭ 2022, задание 6. Касательная к графику функции

Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.
Присоединиться к ExamMe
ОГЭ по Математике
Задание 1. Числа и вычисления (0/10)
Задание 2. Числовые неравенства, координатная прямая (0/10)
Задание 3. Числа, вычисления и алгебраические выражения (0/10)
Задание 4. Уравнения и неравенства (0/10)
Задание 5. Чтение графиков функций (0/10)
Задание 6. Арифметические и геометрические прогрессии (0/10)
Задание 7. Алгебраические выражения (0/10)
Задание 8. Уравнения, неравенства и их системы (0/10)
Задание 9. Треугольники, четырёхугольники, многоугольники и их элементы (0/10)
Задание 10. Окружность, круг и их элементы (0/10)
Задание 11. Площади фигур (0/10)
Задание 12. Фигуры на квадратной решётке (0/10)
Задание 13. Верные и неверные геометрические высказывания (0/10)
Задание 14. Анализ диаграмм, таблиц, графиков (0/10)
Задание 15. Анализ диаграмм, таблиц, графиков (0/10)
Задание 16. Простейшие текстовые задачи (0/10)
Задание 17. Практические задачи по геометрии (0/10)
Задание 18. Анализ диаграмм (0/10)
Задание 19. Статистика и вероятности (0/10)
Задание 20. Расчеты по формулам (0/10)
Задание 21. Алгебраические выражения, уравнения, неравенства и их системы (0/10)
Задание 22. Текстовые задачи (0/10)
Задание 23. Функции и их свойства. Графики функций (0/10)
Задание 24. Геометрическая задача на вычисление (0/10)
Задание 25. Геометрическая задача на доказательство (0/10)
Задание 26. Геометрическая задача повышенной сложности (0/10)
Начать проверочный тест
Найдите площадь пятиугольника,…
Задание:
Найдите площадь пятиугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.).
Ответ дайте в квадратных сантиметрах.
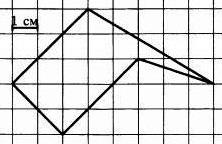
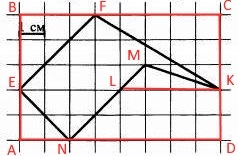
Решение:
Для того чтобы найти площадь данного пятиугольника, Найдем площадь прямоугольника ABCD и вычтем площади прямоугольных треугольников EAM, EBF, FCK, площадь треугольника LMK и площадь трапеции NLKD(см. рис.).
Площадь прямоугольника ABCD равна (произведение длины на ширину) 8*5=40 (кв. см)
Площадь прямоугольного треугольника находится как полупроизведение его катетов.
Таким образом, площадь треугольника EAM равна 1/2*2*2=2 (кв. см)
Площадь треугольника EBF равна 1/2*3*3=4,5 (кв. см)
Площадь треугольника FCK равна 1/2*5*3=7,5 (кв. см)
Площадь треугольника LMK можно найти как полупроизведение стороны на высоту проведенную к этой стороне. Тогда, площадь треугольника LMK равна 1/2*4*1=2 (кв. см.).
Площадь трапеции найдем как полусумму оснований умноженную на высоту : 1/2(4+6)*2=10 (кв. см.).
Тогда площадь искомой фигуры будет равна 40 – 2 – 4,5 – 7,5 – 2 – 10 = 40 – 26 = 14 (кв. см).
Ответ:
14
Задание добавил(а)
![]()
О задание:
Источник условия: Книга: Новый сборник заданий ОГЭ2017. Л.Д. Лапоо, М.А. Попов.
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
Задача 10820 Найдите площадь пятиугольника,…
Условие
![]()
Найдите площадь пятиугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
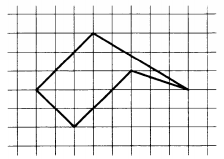
математика 10-11 класс
34617
Решение
Решение
![]()
★
Достраиваем до прямоугольника с размерами 8 и 5
Из площади прямоугольника вычитаем площади прямоугольника с размерами 4 и 2 и площади четырех прямоугольных треугольников (половина произведения катетов) и треугольника с основанием 4 и высотой 1( по формуле половина произведения основания на высоту)
S=8•5-(4•2+(3•3/2)+(2•2/2)+(2•2/2)+(5•3/2)+(4•1/2))=
=40-(8+4,5+2+2+7,5+2)=
=40-26=14
О т в е т. 14 кв. см
Написать комментарий
Найдите площадь пятиугольника, изображённого на клетчатой бумаге с размером клетки 1смх1см (см. рис.). Ответ дайте в квадратных сантиметрах.
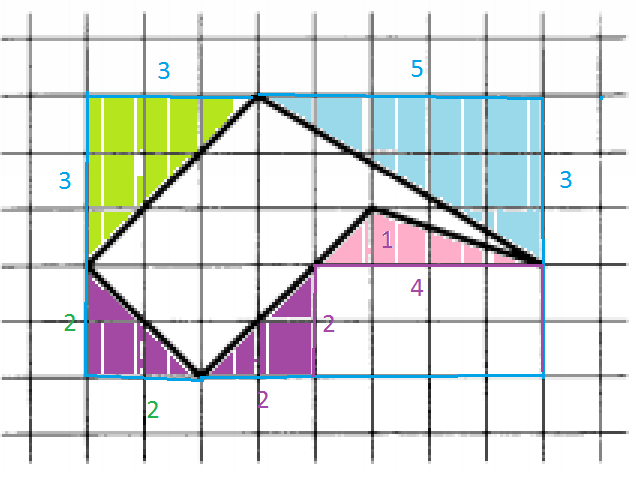
Как известно, диагональ прямоугольника делит его площадь пополам. Поэтому площадь прямоугольных треугольников можно высчитывать как половину от прямоугольника, где гипотенуза является диагональю. Будем искать площади соответствующих
S(желтого)=3⋅32=4,5displaystyle { S( желтого)= frac{3cdot3}{2}= 4,5 }
S(оранжевого)=2⋅22=2displaystyle { S(оранжевого)= frac{2cdot2}{2}= 2 }
S(розового)=2⋅22=2 displaystyle {S(розового)= frac{2cdot2}{2}= 2 }
Чтобы найти площадь оставшейся части фигуры необходимо сделать дополнительное построение до треугольника, от площади которого необходимо отнять площадь дополнительного построения: Вычислим площадь фиолетового треугольника, и вычтем из него площадь зеленого и красного треугольников.
S=3⋅52−12−32=152−12−32=112=5,5displaystyle { S= frac{3cdot5}{2}- frac{1}{2} – frac{3}{2} = frac{15}{2} – frac{1}{2} – frac{3}{2} = frac{11}{2} = 5,5 }
Теперь найдем площадь изначальной фигуры, сложив площади тех частей, на которые мы ее разбили:
S(фигуры)=4,5+2+2+5,5=14S(фигуры) = 4,5 + 2+2 +5,5 = 14
Ответ: 14
Найдите площадь пятиугольника, изображенное на клетчатки бумаге с размером 1×1.
На этой странице вы найдете ответ на вопрос Найдите площадь пятиугольника, изображенное на клетчатки бумаге с размером 1×1?. Вопрос
соответствует категории Алгебра и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
