Как найти площадь пятиугольника по его сторонам

Была ли эта статья полезной?

Как найти площадь пятиугольника

3 методика:ОсновыВычисление площади пятиугольника: геометрияВычисление площади пятиугольника: формула

Пятиугольник – это многоугольник, у которого пять углов. Пятиугольники бывают правильными, неправильными, выпуклыми, вогнутыми, звездчатыми. Не существует простого и единого способа вычисления площади пятиугольников, но легко найти площадь правильного пятиугольника. Эта статья описывает два основных способа вычисления площади правильного пятиугольника.

Шаги

Часть 1 из 3: Основы

1. 
   1
   Правильные и неправильные пятиугольники. Правильный пятиугольник – это пятиугольник, у которого все стороны равны; в противном случае пятиугольник называется неправильным.
   • Правильный пятиугольник всегда будет выпуклым (см. ниже). Неправильный пятиугольник может быть и выпуклым, и вогнутым.
2. 
   2
   Выпуклые и вогнутые пятиугольники. Выпуклый пятиугольник не имеет вершин, направленных внутрь фигуры (другими словами, не имеет внутренних углов более 180 градусов). Вогнутый пятиугольник имеет вершину, направленную внутрь фигуры (другими словами, имеет внутренний угол более 180 градусов).
3. 
   3
   Периметр пятиугольника. Как и в случае других геометрических фигур, найти периметр пятиугольника легко: просто сложите длины всех пяти сторон.
4. 
   4
   Апофема правильного пятиугольника. Апофема – отрезок, соединяющий центр пятиугольника и середину любой из его сторон.
5. 
   5
   Основные тригонометрические функции. Их надо знать, так как площадь пятиугольника можно найти посредством его разбиения на прямоугольные треугольники. Существуют три основных тригонометрических функции: sin угла = противолежащий катет/гипотенуза; cos угла = прилежащий катет/гипотенуза; tg угла = противолежащий катет/прилежащий катет.

Часть 2 из 3: Вычисление площади пятиугольника: геометрия

1. 
   1
   Разбейте пятиугольник на пять равнобедренных треугольников. Затем в каждом треугольнике опустите высоту (из центра пятиугольника). Вы получите десять прямоугольных треугольников. Запомните: каждый угол пятиугольника равен 108 градусам.
   • Например, найдите площадь правильного пятиугольника со стороной 6 см. Для начала разбейте его так, как показано на рисунке.
2. 
   2
   Найдите стороны равнобедренного треугольника. Для этого рассмотрите один из прямоугольных треугольников.
   • В приведенном примере сторона пятиугольника равна 6 см. Следовательно, один катет прямоугольного треугольника равен 3 см (так как высота делит сторону пятиугольника пополам). С помощью тригонометрических функций можно вычислить другие стороны. Вычисления показаны на рисунке.
3. 
   3
   Вычислите площадь прямоугольного треугольника. Площадь прямоугольного треугольника вычисляется по простой формуле: А1 = ab/2.
   • В приведенном выше примере подставьте найденные значения в эту формулу. Вычисления показаны на рисунке.
4. 
   4
   Найдите площадь пятиугольника. Напомним, что вы разбили пятиугольник на десять прямоугольных треугольников. Таким образом, общая площадь пятиугольника в десять раз больше площади одного прямоугольного треугольника: А = 10*А1.
   • В приведенном выше примере площадь пятиугольника вычисляется следующим образом: А = 10*А1 = 10*3,0321 = 30,3210.

Часть 3 из 3: Вычисление площади пятиугольника: формула

1. 
   1
   Формула для вычисления площади любого правильного многоугольника: A = Pa/2, где Р – периметр многоугольника, а – апофема многоугольника.
   • Например, дан правильный пятиугольник со стороной 6 см. Найдите его площадь.
2. 
   2
   Найдите периметр пятиугольника. Для этого сложите длины всех его сторон.
   • В приведенном выше примере: Р = 6+6+6+6+6 = 30.
3. 
   3
   Найдите апофему пятиугольника. Если вы знаете сторону многоугольника, то его апофема вычисляется по формуле: а = s/2tan(180/n), где s – сторона многоугольника, n – количество сторон многоугольника.
   • В приведенном выше примере вычисление апофемы показано на рисунке.
4. 
   4
   Вычислите площадь пятиугольника. Для этого используйте основную формулу для вычисления площади пятиугольника.
   • В приведенном выше примере: А = (30*2,0214)/2 = 30,3210.

Советы

• Если возможно, вычислите площадь пятиугольника, используя оба описанных метода. Затем сравните результаты, чтобы подтвердить правильность ответа.

Содержание

• Как найти площадь правильного пятиугольника?
• Площадь правильного пятиугольника, знающая сторону a
• Площадь правильного пятиугольника, зная его радиус
• Как рассчитать площадь неправильного пятиугольника?
• Триангуляция
• Гауссовские детерминанты
• Решенные упражнения
• Упражнение 1
• Решение
• Упражнение 2.
• Решение
• Площадь треугольника EDC
• Площадь треугольника AEC
• Площадь треугольника ABC
• Площадь неправильного пятиугольника
• Ссылки

Для расчета площадь пятиугольника для начала нам нужно определить, регулярно это или нет. Пятиугольник – это многоугольник, замкнутая плоская фигура с пятью сторонами. Когда многоугольник правильный, это означает, что длина его сторон одинакова, а его внутренние углы одинаковы.

В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.

Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.

Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.

Еще одна процедура для вычисления площадей полигонов в целом, зная координаты их вершин, – это метод, называемый Гауссовские детерминанты, о котором мы расскажем позже.

Как найти площадь правильного пятиугольника?

Мы собираемся взять правильный пятиугольник со стороной a и разделить его на 5 равных треугольников, как показано на рисунке, проведя отрезки от центра (красный) до вершин (синий).

В свою очередь, треугольники, как и тот, который выделен желтым справа на рисунке выше, делятся на два равных прямоугольных треугольника благодаря зеленому сегменту, который называется апофема.

Апофема определяется как перпендикулярный сегмент, который соединяет центр многоугольника с центром одной из сторон. Его длина L_К.

Площадь прямоугольного треугольника с основанием a / 2 и высотой L_К это:

[(a / 2) x L_К]

Пентагон состоит из 10 таких треугольников, поэтому его площадь равна:

А = 10 (а / 2) х L_К

Но периметр п пятиугольника равно P =10а, поэтому площадь определяется как произведение периметра и длины апофемы:

А = P x L_К /2

Площадь правильного пятиугольника, знающая сторону a

Выражая длину апофемы L_К как функция стороны a, зная, что указанный угол составляет половину центрального угла, то есть 36º, что эквивалентно:

36º = π/5

Методом элементарной тригонометрии через тангенс острого угла 36º:

загар (π / 5) = (a / 2) ÷ L_К

Отсюда:

L_К=  (а / 2) ÷ загар (π / 5)

Подставив в область, выведенную в предыдущем разделе, и зная, что P = 5a:

А = P x L_К /2

Площадь правильного пятиугольника, зная его радиус

В радио правильного многоугольника – это отрезок, идущий от центра до одной из его вершин. Он соответствует радиусу описанной окружности, как показано на следующем рисунке:

Пусть R – мера указанного радиуса, которая совпадает с гипотенузой прямоугольного треугольника, выделенного синим цветом на предыдущем рисунке. По тригонометрии:

cos 36º = cos (π / 5) = L_К ÷ R

Y

sin 36º = sin (π / 5) = (a / 2) ÷ R

Таким образом:

А = P x L_К / 2 = 5р. sin (π / 5) x R. cos (π / 5) = 5R² [sin (π / 5) x cos (π / 5)]

Используя формулу двойного угла:

грех (2θ) = 2 греха θ. cos θ

У нас это:

[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º

Итак, подставив это значение, мы получим следующую формулу для площади правильного пятиугольника:

А = (5/2) R².sen 72º

Как рассчитать площадь неправильного пятиугольника?

Как мы уже говорили ранее, для неправильного многоугольника не существует уникальной формулы, но есть два метода, которые обычно работают очень хорошо: первый называется триангуляцией, а второй – методом детерминантов Гаусса.

Триангуляция

Он состоит из деления фигуры на треугольники, площадь которых легче вычислить, или ее также можно проверить с другими фигурами, площадь которых известна, такими как квадраты, прямоугольники и трапеции.

Гауссовские детерминанты

Другой способ найти площадь неправильного пятиугольника или другого неправильного многоугольника – это поместить фигуру в декартову систему координат, чтобы найти координаты вершин.

Зная эти координаты, применяется гауссовский метод определителей для вычисления площади, которая определяется следующей формулой:

Где A – площадь многоугольника, а (x_п , Y_п ) – координаты вершин. Многоугольник с n сторонами имеет 5 вершин, для пятиугольника это будет n = 5:

Полосы, сопровождающие формулу, представляют собой столбцы модуля или абсолютного значения.

Это означает, что даже если результат операции отрицательный, мы должны выразить его положительным знаком, а если он уже положительный, то его нужно оставить с этим знаком. Это потому, что площадь всегда является положительной величиной.

Процедура названа гауссовскими детерминантами в честь ее создателя, немецкого математика Карла Ф. Гаусса (1777-1855). Указанные операции эквивалентны определителю матрицы 2 × 2, например, первый определитель равен:

Чтобы найти площадь пятиугольника, мы должны решить 5 определителей, сложить результат алгебраически, разделить его на 2 и, наконец, выразить площадь всегда с положительным знаком.

Решенные упражнения

Упражнение 1

Найдите площадь правильного пятиугольника, апофема которого равна 4 см, а сторона – 5,9 см.

Решение

Поскольку это правильный пятиугольник, а у нас есть размеры стороны и апофемы, мы используем формулу, полученную выше:

А = P x L_К /2

Периметр P равен 5a = 5 x 5,9 см = 29,5 см.

A = 29,5 см x 4 см / 2 = 59 см²

Упражнение 2.

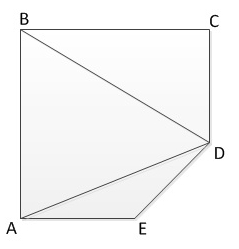
Найдите площадь неправильного пятиугольника, как показано. Известны следующие размеры:

DC ≈ DE

АЕ = АВ = 5

BC = 12

Решение

Площадь пятиугольника – это сумма площадей треугольников, которые являются прямоугольниками. В заявлении говорится, что DC ≈ DE, поэтому при применении теоремы Пифагора к треугольнику EDC мы имеем:

EC² = 2 ED². Тогда EC = √2.ED.

Треугольники AEC и ABC имеют общую гипотенузу – отрезок AC, поэтому:

EA² + EC² = AB² + BC²

Поскольку EA и AB измеряют одно и то же, отсюда следует, что:

EC = BC = √2.ED

Поскольку BC = 12, то ED = 12 / √2 = 8,485.

Используя эти значения, мы рассчитаем площадь каждого треугольника и добавим их в конце.

Площадь треугольника EDC

ED x DC / 2 = 8,485² / 2 = 36

Площадь треугольника AEC

EA x EC / 2 = EA x √2. ED / 2 = 5 x √2. 8 485/2 = 30

Площадь треугольника ABC

AB x BC / 2

Тогда искомая область:

5 х 12/2 = 30

Это то же самое, что и треугольник AEC, поскольку они оба имеют одинаковые размеры.

Площадь неправильного пятиугольника

Наконец, запрашиваемая площадь представляет собой сумму площадей трех треугольников:

А = 36 + 30 + 30 единиц = 96 единиц.

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Открытый справочник по математике. Площадь многоугольника. Получено с: mathopenref.com.
3. Формулы Вселенной. Площадь неправильного пятиугольника. Получено с: universaloformulas.com.
4. Формулы Вселенной. Площадь правильного пятиугольника. Получено с: universaloformulas.com.
5. Википедия. Пентагон. Получено с: es.wikipedia.com.

Площадь пятиугольника (пентагона).

Пятиугольник (пентагон) — представляет собой геометрическую фигуру с пятью углами. существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным.

Формула расчёта площади пятиугольника (пентагона) зная длину сторон: S=n/4 × a 2 × ctg(pi/n).
Где (S) — площадь пятиугольника, (n) — количество сторон, в нашем случае 5, (a) — длина стороны, (ctg) — котангенс.

Формула расчёта площади пятиугольника (пентагона) зная радиус вписанной окружности: a = 1,4131 × r.
Где (r) — радиус вписанной окружности, дальше используем формулу расчёта площади пятиугольника (пентагона)

Формула расчёта площади пятиугольника (пентагона) зная радиус описанной окружности: a = 1,1756 × r.
Где (r) — радиус вписанной окружности, дальше используем формулу расчёта площади пятиугольника (пентагона)

Калькулятор для расчёта площади пятиугольника (пентагона), онлайн

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Как найти площадь пятиугольника — математический — 2022

Чтобы найти область правильного пятиугольника с пятью равными сторонами и углами, вы должны знать длину каждой стороны и длину линии от центра каждой стороны до центра пятиугольника.

Отметьте среднюю точку правильного пятиугольника и проведите линию от каждого из углов до средней точки. Если вы не знаете середину, вы можете нарисовать линии к середине противоположной стороны и стереть половину.

Возьмите одну из этих линий и вытяните ее, чтобы коснуться средней точки противоположной стороны. Это создает апофе Сделайте это для каждой линии, чтобы создать 10 маленьких прямоугольных треугольников с одинаковой площадью. Чтобы продолжить, вы должны знать длину апофема. Если вы работаете с физическим пятиугольником, измерьте апофим.

Найдите площадь одного прямоугольного треугольника и умножьте на 10, чтобы получить общую площадь пятиугольника. Площадь прямоугольного треугольника определяется по формуле: 1/2 x база x высота. Высота — это апофема, а основание — половина стороны пятиугольника.

подсказки

Тот же метод применяется к неправильным пятиугольникам, за исключением того, что вы разбиваете пятиугольник на треугольники разных размеров, находите площадь каждого отдельного треугольника и добавляете области для общей площади пятиугольника.

Как найти площадь 12-стороннего многоугольника

Многоугольник — это любая двумерная замкнутая фигура с тремя или более замкнутыми сторонами, а 12-сторонний многоугольник — это додекагон. Существует формула для расчета площади правильного додекагона, равного сторонам и углам, но не для определения площади неправильного додекагона.

Как найти площадь 3-мерного прямоугольника

Многие трехмерные объекты имеют двухмерные формы в виде деталей или компонентов. Прямоугольная призма — это трехмерное тело с двумя одинаковыми и параллельными прямоугольными основаниями. Четыре стороны между двумя основаниями также являются прямоугольниками, причем каждый прямоугольник идентичен тому, который расположен напротив него. Прямоугольный .

Каковы характеристики пятиугольника, шестиугольника и восьмиугольника?

Полигоны — это математические понятия, относящиеся к прямолинейным геометрическим фигурам. Полигоны включают такие фигуры, как пятиугольники, шестиугольники и восьмиугольники. Полигоны можно считать выпуклыми, вогнутыми или правильными. Полигоны могут иметь более одной характеристики. Например, правильный пятиугольник также считается выпуклым.

Площадь многоугольника

Калькулятор считает площадь многоугольника по введенным вами сторонами и диагоналям, главное чтобы диагонали делили многоугольник на несколько треугольников, которые в свою очередь не пересекались бы между собой.

И так, глядя на рисунок, можно сразу представить, что площадь данного многоугольника будет равна сумме площади трех треугольников, расположенных внутри многоугольника.

Для начала расчетов вам придется внимательно внести в таблицу значения сторон ваших треугольников.