Как найти площадь пятиугольника по координатам вершин - Сайт, где вы сможете решить свои вопросы

Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.

Принцип работы остается таким же – многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон – Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку. Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже

Четырехугольник

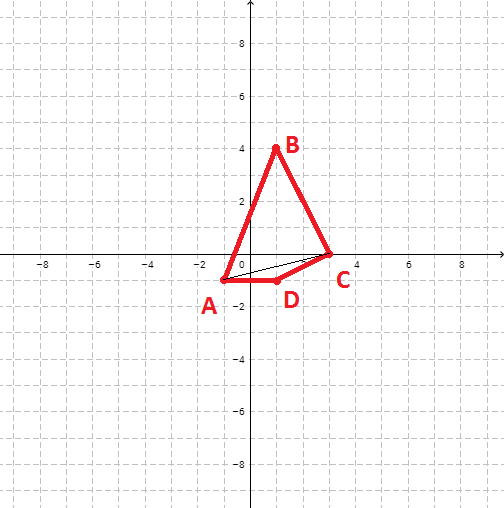
При добавлении следующей точки, например, так, как на следующем рисунке

Пятиугольник

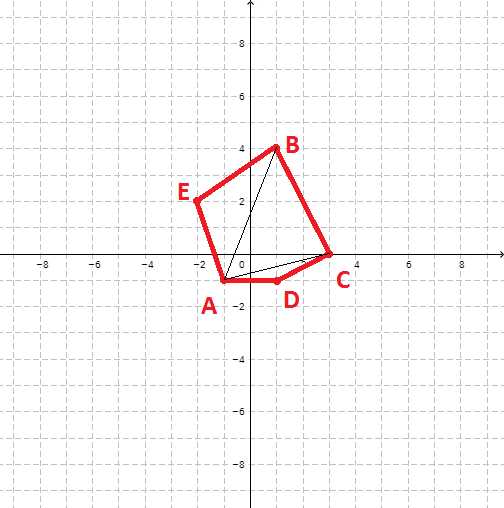
должен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.

Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.

Алгоритм работает за время O(nh) , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет O(n^2) . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.

Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника. Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.

Вычисление площади выпуклого многоугольника по координатам вершин на плоскости

Точки многоугольника

	Точка	X	Y

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Источник

Geometry is a branch of mathematics that is all about the study of shapes. In general, we study two types of shapes in geometry one is the flat shape and the other solid shapes. Flat shapes are plotted on flat surfaces which are two-dimensional and solid shapes are three-dimensional. Geometry also deals with the parameters of these shapes. It gives standard formulas for determining their parameters like area, perimeter, volume, etc.

The given article deals with one of the flat shapes pentagons. It gives a brief description of the pentagon and its properties. The article explains the area formula of a pentagon along with some sample problems for better understanding.

What is a Pentagon?

The word pentagon denotes ‘five angles’ as “Penta” means five and “gon” means angles. It is a geometrical shape having five sides and five angles. It is a five-sided self-intersecting polygon. And, the sum of all the interior angles of a polygon measures to be 540 degrees.

Summing up, a pentagon is a five-sided, two-dimensional geometrical shape whose interior angles sum up to be 540 degrees.

Properties of a pentagon

A pentagon has five sides.
It has 5 diagonals meeting at the same point.
The interior angles of a pentagon measure to be 72 degrees.
the exterior angles of a pentagon measure to be 108 degrees.

How To find the Area of Pentagon?

Using Apothem Length

The area of a pentagon is determined by its side and apothem length. The formula of the area of a pentagon is derived by multiplying any side and apothem length by 5/2.

Mathematically the formula is given by

Area of pentagon(A)=(5/2) s × a

where,

s is the side

and a is apothem length

Pentagon

For example:

If a side of a pentagon is 12cm and its apothem length is 6cm, the area of the pentagon can be determined by

Area of pentagon= (5/2) × side × apothem length

= (5/2) × 12 × 6

= 180cm²

Using only Side Length

The area of the pentagon can also be calculated only by using the length. Here, to calculate the area of the given pentagon by using only the side length following formula is used

$Area=frac{1}{4}sqrt{5(5+2sqrt5)}s^2$

where,

s is the side length

For example:

If a pentagon is given having side length of 5cm, the area of the pentagon can be determined by

Area of pentagon = $frac{1}{4}sqrt{5(5+2sqrt5)}s^2$

= $frac{1}{4}sqrt{5(5+2sqrt5)}(5)^2$

= 43.01cm²

Sample Problems

Problem 1. Find the area of a pentagon with a side 5cm and apothem length 4cm.

Solution:

Given

Side of pentagon = 5cm

apothem length = 4cm

We have,

Area = (5/2) × s × a

=>A = (5/2) × 5 × 4

=>A = 50cm²

Problem 2. Find the area of a pentagon with a side 12cm and apothem length of 6cm.

Solution:

Given

Side of pentagon = 12cm

apothem length = 6cm

We have,

Area = (5/2) × s × a

=>A = (5/2) × 12 × 6

=>A = 180cm²

Problem 3. Find the area of a pentagon with a side 12cm and apothem length of 4cm.

Solution:

Given

Side of pentagon = 12cm

apothem length = 4cm

We have,

Area = (5/2) × s × a

=>A = (5/2) × 12 × 4

=>A = 120cm²

Problem 4. Find the area of a pentagon with a side 10cm and apothem length of 5cm.

Solution:

Given

Side of pentagon = 10cm

apothem length = 5cm

We have,

Area = (5/2) × s × a

=>A = (5/2) × 10 × 5

=>A = 125cm²

Problem 5. Find the area of a pentagon with a side 8cm and apothem length of 5cm.

Solution:

Given

Side of pentagon = 8cm

apothem length = 5cm

We have,

Area = (5/2) × s × a

=>A = (5/2) × 8 × 5

=>A = 100cm²

Problem 6. Find the area of a pentagon with a side length of 4cm.

Solution:

Given

Side length of pentagon is 4cm

We have,

Area of pentagon = $frac{1}{4}sqrt{5(5+2sqrt5)}s^2$

=> $frac{1}{4}sqrt{5(5+2sqrt5)}4^2$

=>27.52cm²

Problem 7. Find the area of a pentagon with a side length of 6cm.

Solution:

Given,

Side length of pentagon is 6cm.

We have,

Area of pentagon = $frac{1}{4}sqrt{5(5+2sqrt5)}s^2$

=> $frac{1}{4}sqrt{5(5+2sqrt5)}6^2$

=>61.93cm²

Last Updated :
01 Feb, 2022

Like Article

Save Article

Источник

Option Strict On
Option Explicit On
Imports System.Math
Public Class Form1
    'функция ввода значения 
    Function vvod(ByVal t As TextBox) As Double
        Return Val(t.Text)
    End Function
    'функция вывода результата в textbox
    Sub vivod(ByVal S As Double, ByVal t As TextBox)
        t.Text = CStr(S)
    End Sub
    'функция вычисления значение биссектрисы L(a,b,c)
    Public Function Labc(ByVal x1 As Double, ByVal y1 As Double, ByVal x2 As Double, ByVal y2 As Double, ByVal x3 As Double, ByVal y3 As Double) As Double
        Return CDbl(1 / 2 * (Abs(x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)))
    End Function
 
    Sub PS(ByVal x1 As Double, ByVal y1 As Double, ByVal x2 As Double, ByVal y2 As Double, ByVal x3 As Double, ByVal y3 As Double)
        Dim x1, x2, x3, y1, y2, y3, x4, y4, x5, y5, As Double
        Dim s, s1, s2, s3 As Double
        Dim z1, z2, z3, z4 As Double
       
        x1 = vvod(TextBox1)
        y1 = vvod(TextBox2)
        x2 = vvod(TextBox3)
        y2 = vvod(TextBox4)
        x3 = vvod(TextBox5)
        y3 = vvod(TextBox6)
        s1 = Labc()
        s2 = Labc()
        s3 = Labc()
 
 
 
 
        s = s1 + s2 + s3
 
 
 
 
        vivod(s, TextBox11)
    End Sub
 
    Private Sub Button2_Click(ByVal sender As Object, ByVal e As System.EventArgs) Handles Button2.Click
        End
    End Sub
End Class

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 января 2022 года; проверки требуют 2 правки.

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии, лесном хозяйстве и других областях.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение[править | править код]

Формула может быть представлена следующим выражением:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}right|=\&={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+dots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-dots -x_{n}y_{n-1}-x_{1}y_{n}|,end{aligned}}}$

где

S — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1]^[2]:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}left|sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1})right|=\&={frac {1}{2}}left|sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}right|=\&={frac {1}{2}}left|sum _{i=1}^{n}det {begin{pmatrix}x_{i}&y_{i}\x_{i+1}&y_{i+1}end{pmatrix}}right|,end{aligned}}}$

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры[править | править код]

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

${displaystyle mathbf {S} _{text{tri.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,}$

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

${displaystyle mathbf {S} _{text{pent.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|.}$

S для четырехугольника — переменные до x₄ и y₄:

${displaystyle mathbf {S} _{text{quad.}}={frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.}$

Более сложный пример[править | править код]

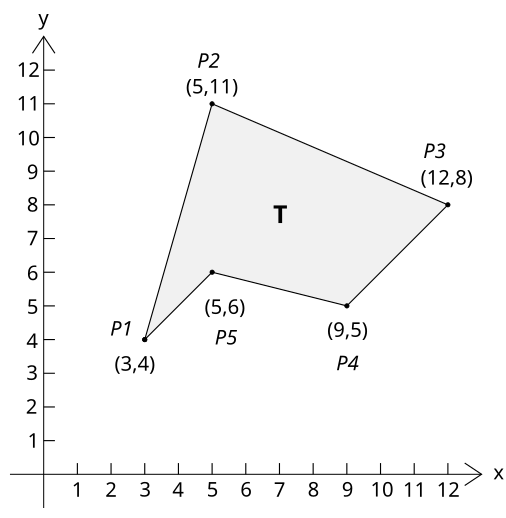
Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

${displaystyle {begin{aligned}mathbf {S} &={frac {1}{2}}|3times 11+5times 8+12times 5+9times 6+5times 4-{}\&qquad -4times 5-11times 12-8times 9-5times 5-6times 3|=\&={frac {60}{2}}=30.end{aligned}}}$

Объяснение названия[править | править код]

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

${displaystyle {begin{bmatrix}2&4\3&-8\1&2\2&4end{bmatrix}}.}$

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание “Шнуровки Гаусса” представлено в видео на канале Wild Mathing [1]

См. также[править | править код]

Планиметр
Теорема Грина

Примечания[править | править код]

↑ Shoelace Theorem Архивная копия от 23 сентября 2020 на Wayback Machine, Art of Problem Solving Wiki.
↑ Weisstein, Eric W. Polygon Area. Wolfram MathWorld. Дата обращения: 24 июля 2012. Архивировано 12 мая 2012 года.
↑ Richard Rhoad; George Milauskas; Robert Whipple. Geometry for Enjoyment and Challenge. — new. — McDougal Littell (англ.) (рус., 1991. — С. 717—718. — ISBN 0-86609-965-4.

Источник

Тема
занятия:

Площадь
многоугольника через определитель второго порядка.

Цель:1. Вывод формулы площади
треугольника через определитель II-го порядка с применением
формул тригонометрии.

2.Самостоятельная творческая
работа по разработке формул площадей четырехугольника, пятиугольника,
квадрата, правильного шестиугольника, n-угольника с
использованием определителя II-го порядка.

3. Научить учащихся способу вычисления площади четырехугольника с координатами
его вершин для использования на ЕГЭ.

I. Введение. На уроках алгебры мы познакомились
с необычным способом решения систем двух линейных уравнений с двумя
переменными с помощью определителя второго порядка.

Использование определителей оказалось
удивительно полезным и интересным при решении и анализе систем.

А используется ли понятие определителя
в геометрии?

Постараемся сегодня ответить на этот вопрос.

II. Объяснение нового материала. Вывод
формулы площади треугольника через определитель II-го
порядка в прямоугольной системе координат.

Создание проблемы.

Площадь треугольника

Определителем второго порядка называют
значение разности произведений чисел

a∙d – b∙c, записываемых для
удобства вычислений в виде таблички из четырех чисел..

Выведем формулу площади треугольника в виде определителя,
составленного из разности координат вершин треугольника.

Докажем, что площадь треугольника равна:

Пусть в прямоугольной системе координат А(х_1,у₁),
В(х₂,у₂), С (х₃,у₃) – вершины
треугольника. Найти площадь треугольника АВС.

Обозначим стороны треугольника через АС=b, АВ =с и угол между ними через ВАС=φ,
по известной формуле тригонометрии получим: S= ½ bс∙sinφ.

Угол φ можно представить в виде разности: φ =
β-α, где α и β – углы, образованные соответственно сторонами АВ и АС с осью Ох.

Поэтому S =½ bс∙sin ( β-α) =½bс∙(sinβ∙ cosα – cosβ∙sinα).

Из рисунка имеем

c∙ cosα= АВ₂=А₁В₁= х_{2 –}х₁,

с∙ sinα=В₂В =
у₂-у₁,

b∙ cosβ=АС₂=А₁С₁=х₃-х₁,

b∙ sinβ=С₂С=у₃-у₁.

Следовательно, S=½((х₂—х₁)(у₃-у₁)-(х₃-х₁)(у₂-у₁).

Заметим, что эта формула при ином расположении
вершин может дать площадь треугольника S со знаком
«минус».

Поэтому формулу площади треугольника запишем
в виде S =±½((х₂—х₁)(у₃-у₁)-(х₃-х₁)(у₂-у₁),
где знак выбирается так, чтобы для площади получалось положительное число.

Используя понятие определителя второго порядка
= аd–bс, формулу можно записать в удобной для запоминания форме:

S треуг. = ±.

Постановка проблемы: определить площадь
четырехугольника , пятиугольника, квадрата, правильного шестиугольника, n-угольника через координаты их вершин.

Рекомендации: Определение
площади многоугольника сводится к определению площадей треугольников. Для этого
достаточно разбить многоугольник на треугольники, площади которых вычисляют по
найденной формуле. Правильный шестиугольник разбивается на равные
четырехугольники

II. Учащиеся. Самостоятельное решение
проблемы (работа учащихся в группах дифференцировано:
продвинутый уровень-площадь четырехугольника и пятиугольника, базовый
уровень-площадь четырехугольника, шестиугольника, квадрата).

1.Площадь четырехугольника

Выведем формулу для вычисления площади
четырехугольника на примере трапеции.

Пусть трапеция задана координатами своих
вершин в прямоугольной системе координат.

Диагональ разделит трапецию на два
треугольника, площади которых найдем через определитель.

₌

_{Запишем выражение в удобной для запоминания форме, в

виде определителя}

(х₁у₁)
(х₂у₂)

(х₄у₄)
(х₃у₃₎

_{Вывод: Площадь четырехугольника равна половине определителя, элементами

столбцов и строк которого является

разность координат вершин четырехугольника, взятых по диагонали.}

_{Нумерацию координат можно рассмотреть в любом порядке.}

_{Пример. Вычислить

площадь четырехугольника с координатами его вершин}

₍₁_;_{1), (3}_;_{4), (6}_;3)_{, ((3}_;1)_.

_{По формуле через

определитель}

_{Сделаем

проверку, вычислив площадь трапеции как сумму площадей, через высоты

треугольников.}

_{Получили равные

ответы.}

_{2. Площадь

правильного шестиугольника.}

_{Площадь

правильного шестиугольника найдем как сумму площадей двух равных

четырехугольников.}

_{Площадь

ромба, квадрата или параллелограмма находятся аналогично, разбиением фигуры на

равные треугольники.}

_{3. Площадь

квадрата.}

_{.Если центр многоугольника

расположен в начале координат, то формула площади многоугольника записывается

с помощью координат одной или двух вершин:}