- Авторы
- Файлы
Исаев Ю.М.
Гришин О.П.
Настин А.А.
В общем случае пятно контакта недеформируемого инструмента с пластичной поверхностью представляют собой пространственную фигуру, образованную на инструменте (торе, цилиндре, шаре) пересечением пластичной поверхности детали – чаще всего цилиндра. Поэтому для нахождения площади пятна контакта необходимо решать задачу о пересечении двух пространственных фигур. При электромеханической обработке наиболее часто применяется инструмент, рабочая поверхность которого представляет собой поверхность тора. При обработке деталей типа втулок обрабатываемая поверхность представляет собой цилиндр.
Рассмотрим поверхность контакта торсионного вала и ролика в виде тора по внешней поверхности цилиндра.
Уравнение поверхности тора, внедряемой в торсионный вал, в декартовой системе координат запишется:
Переходя к цилиндрической системе координат, найдем частные производные:
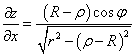
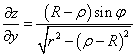
Далее находим элемент площади
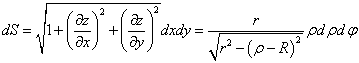
Вычисляем площадь поверхности в цилиндрической системе координат по формуле:
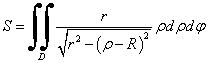
Область интегрирования D ограничена с одной стороны уравнением окружности сечения цилиндра, а с другой стороны уравнением внешней окружности тора ρ = R, тогда в полярной системе координат площадь поверхности пятна вычисляется по формуле:
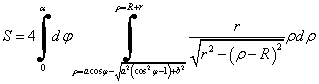
Для нахождения предельного угла интегрирования α найдем координаты точек пересечения окружности цилиндра и окружности тора.
Площадь пятна контакта определяется как сумма площадей контакта в зонах пластической и упругой деформации. Сначала найдем площадь пятна контакта в зоне пластической деформации при заданных значениях размеров вала и ролика (в мм ).
,
,
,
,
мм2
Затем найдем площадь пятна контакта в зоне упругой деформации при b = 29,55:
мм2
Общая площадь пятна контакта: мм2
Библиографическая ссылка
Исаев Ю.М., Гришин О.П., Настин А.А. РАСЧЕТ ПЛОЩАДИ ПЯТНА КОНТАКТА ИНСТРУМЕНТА ПО ВНЕШНЕЙ ПОВЕРХНОСТИ ЦИЛИНДРИЧЕСКОЙ ДЕТАЛИ // Современные наукоемкие технологии. – 2008. – № 2.
– С. 135-136;
URL: https://top-technologies.ru/ru/article/view?id=23270 (дата обращения: 16.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Методика расчета
Для
заданного значения натяга
необходимо определить угол наклона
ролика, обеспечивающего заданное
значение площади пятна контакта
.
Для вычисления
площади пятна контакта, описываемой
уравнениями (1.6) и (1.7), используется метод
трапеций. Площадь пятна контакта
определяется по формуле:
,
(1.8)
где
,
– определяются
по уравнениям
(1.6), (1.7);
n
– число шагов интегрирования или число
участков, на которые разбивается площадь
пятна контакта.
Изменяя
значение угла контакта ролика
от
90° до
заданного
с шагом
1° – 5°,
вычисляем площадь пятна контакта по
формулам
(1.1 – 1.8)
для каждого угла
от
90° до
.
В результате получим зависимость площади
от угла
.
Эту зависимость можно проиллюстрировать
графически (рис.
2).
По
графику определяется угол
,
обеспечивающий
заданную площадь
пятна
контакта
.

Рис.
2. График зависимости
от
Порядок выполнения работы
1.
Составить алгоритм и программу расчета
пятна контакта.
2.
Для своего варианта по табл.
1
определить значения
,
и
.
3.
Выбрать типоразмер ролика по табл.
2.
4.
По вычисленным значениям
для различных углов
построить график (рис. 2).
5.
По графику (рис.
2) определить
значения угла
,
обеспечивавшего заданное значение
.
6.
Если
,
то необходимо взять другой типоразмер
ролика и повторить расчеты.
7.
На рис. 1 указать полученные значения
параметров.
Содержание отчета
1.
Алгоритм и программа расчета.
2.
Номер
варианта задания и исходные значения
параметров.
3.
Вариант типоразмера ролика.
4.
Вычисленные значения
и
при выбранном числе
.
5.
График зависимости
от
.
6.
Найденное значение параметра
.
Таблица 1
|
№ варианта |
|
, |
, |
|
1 |
60 |
0,05 |
2,50 |
|
2 |
50 |
0,07 |
3,50 |
|
3 |
45 |
0,08 |
4,10 |
|
4 |
55 |
0,05 |
2,60 |
|
5 |
70 |
0,06 |
2,95 |
|
6 |
55 |
0,15 |
7,67 |
|
7 |
40 |
0,03 |
1,65 |
|
8 |
65 |
0,06 |
3,00 |
|
9 |
45 |
0,14 |
7,30 |
|
10 |
50 |
0,10 |
5,25 |
|
11 |
40 |
0,10 |
5,00 |
|
12 |
45 |
0,03 |
1,55 |
|
13 |
50 |
0,01 |
0,5 |
|
14 |
60 |
0,05 |
2,1 |
|
15 |
50 |
0,02 |
1,6 |
|
16 |
45 |
0,07 |
3,9 |
|
17 |
55 |
0,16 |
7,2 |
|
18 |
40 |
0,2 |
1,6 |
|
19 |
70 |
0,05 |
3,1 |
|
20 |
65 |
0,07 |
3,3 |
Таблица 2
|
Параметры, |
Тип ролика |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
R |
25 |
30 |
20 |
34 |
25 |
33 |
|
r |
4 |
5 |
3 |
6 |
5 |
4 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
30.04.2022600.58 Кб027.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
УДК 621.81.004.1; 621.(075.8)
В.М. Грязев, бакалавр, (8472) 33-23-10, tms@tsu.tula.ru (Россия, Тула, ТулГУ)
МЕТОДИКА ОПРЕДЕЛЕНИЯ ПЛОЩАДИ ПЯТНА КОНТАКТА С УЧЕТОМ ПОГРЕШНОСТЕЙ ПОЛОЖЕНИЯ И ФОРМЫ КОНТАКТИРУЮЩИХ ПОВЕРХНОСТЕЙ
Дано аналитическое описание зависимостей влияния погрешностей положения и формы контактирующих поверхностей на контурную и относительную площадь пятна контакта сопрягаемых поверхностей, измеряемую по отпечатку копоти. Приведено решение обратной задачи – определение допустимых погрешностей положения и формы контактирующих поверхностей при заданном пятне контакта.
Ключевые слова: копоть, пятно контакта, погрешности формы, погрешности положения.
Обеспечение высокого уровня технологичности изделий должно начинаться на стадии проектирования изделия. В работах [1-4] было показано, что требуемая полнота контакта поверхностей взаимодействующих деталей может быть обеспечена при назначении на параметры взаимодействующих деталей соответствующих норм точности. Решается, следовательно, задача определения контура отпечатка, если известны погрешности формы и расположения сопрягаемых поверхностей, а также толщина слоя копоти. Методикой такого расчёта должен обладать технолог для обоснования заданных конструктором норм точности.
Та же расчётная методика может быть использована и для решения обратной задачи, когда по регламентированным размерам и формам пятна контакта требуется определить допускаемые погрешности формы и расположения сопрягаемых поверхностей. Ниже рассматриваются случаи контактного взаимодействия различных видов поверхностей. В целях простоты изложения сначала рассматривается взаимодействие идеальных поверхностей, разделённых промежуточным слоем копоти. Такое начальное допущение об идеальности формы взаимодействующих поверхностей сделано для упрощения расчётных операций.
Рассмотрим контакт плоских поверхностей. Если одна из сопрягаемых поверхностей А (рис. 1,а) отклонена от номинальной поверхности контакта Б на величину А в одном направлении, то пятно контакта будет иметь форму прямоугольника со сторонами 1к и Номинальная площадь пятна контакта равна:
Фа = 1к ‘ 12ш (1)
Длина расположения границы контакта в направлении раскрытия стыка – 1к определяется из условия, что А’ = Ьк, т.е.:
l = h¿K_
к А
где bK – толщина нанесенного слоя копоти.
Следовательно, контурная площадь пятна контакта будет равна:
¡Л ■ ¡2 ■ l
Ф = ¡1 ¡2 ¡K (2)
с А
Относительная контурная площадь пятна контакта, выраженная в процентах по отношению к номинальной Фа, равна:
фо = loo А % (3)
Аналогичным образом определяются границы участка контакта, если обе сопрягаемые поверхности имеют отклонения А1 и А2 относительно номинальной поверхности контакта (рис. 1, б). В этом случае контурная площадь контакта:
^ ¡Л ■ ¡2 ■ bK
Фс = —к (4)
= ¡1 • ¡2 • bK
с Al + А 2 b
Ф0 = 100 —-+— % (5)
Д1 + А 2
При отклонении одной из сопрягаемых поверхностей от номинальной поверхности контакта в двух направлениях на Д1 и А 2 (рис. 1, в) пятно контакта будет иметь форму треугольника, контурная площадь которого равна:
2
Фс = ^ (6)
А1 – А 2
Относительная контурная площадь пятна контакта равна:
Фо =Д°А1% (7)
А1 – А 2
В случае если обе сопрягаемые поверхности имеют погрешности по двум направлениям – А1, А2 и А”, А 2 (рис. 1, г), то будем иметь:
0,5/1 -12 – Ь1
Фс = 7-—к-ч (8)
С (А1 +А1 )-(А2 +А2)
Ф0 = 7–ч % (9)
0 (А1 +А1 )-(А2 +А2)
Рассмотрим контакт, плоской поверхности с выпуклой в предположении, что последняя имеет постоянный радиус кривизны R (рис. 2.,а). В этом случае пятно контакта имеет вид прямоугольника со сторонами 1к и 12.
<1
г 4
/
1
ш
ф
а!
5е
А А
Нс2
Ф
тг
>
б)
Ф
г)
Рис. 2. К расчёту площади пятна контакта при сопряжении деталей, имеющих выпуклость рабочих поверхностей
Раскрытие стыка А’ = ЬК на границе пятна контакта равно:
1К = 2^2ЬК-Я’-Ь1 . (10)
Значение радиуса входящего в формулу (10), можно приближённо выразить через выпуклость А и длину детали в продольном направлении
Я’ = Я + Ък
п
8Д + Ьк
(П)
После подстановки (11) в (10) при допущении, что Ък =0 (поскольку Ьк « 1), получим:
/ -/ Ь* ‘к ~п
(12)
Тогда с учётом (12) контурная площадь пятна контакта будет равна:
фс=11-ь№
V А
Относительная контурная площадь пятна контакта равна:
[а
Ф0 =100, М-% (14)
V А
В случае если в продольном направлении обе сопрягаемые поверхности имеют выпуклости А^ и А2? как это показано на рис. 2, б, то
а Фс и Ф0 соответственно равны:
(16)
Л1 Ах+ А2
V А1+А2
При сопряжении плоской поверхности с поверхностью, имеющей выпуклость в продольном и поперечном направлениях А^ и А2 (рис. 2, в), контурная площадь пятна контакта будет равна площади эллипса с осями 1кх и 1к2 > т-е:
Фс=0,25к1К1-1К2 (18)
Протяжённость пятна контакта в продольном и поперечном направлениях: / и определяется с учётом выпуклости и длины поверхности
в соответствующем направлении по формуле (12), т.е:
(19)
1к2 =’2.
Ък
к (20)
1Л2
После подстановки значений 1К и 1К из формул (19) и (20) в формулу (18) получим выражение для контурной площади пятна контакта
Ф.
с
0,25кЪк -12 д/Л1 * А2
(21)
Относительная контурная площадь пятна контакта для рассматриваемого случая сопряжения поверхностей равна:
ф*=° (22)
Аналогичным образом определяется площадь пятна контакта для
136
других случаев сопряжения поверхностей взаимодействующих деталей.
Рассмотренные примеры иллюстрируют постановку проверочной задачи, когда по известным погрешностям положения и формы контактирующих поверхностей определяются параметры пятна контакта.
В ходе проектирования вероятна задача и в другой постановке, когда для заданного размера пятна контакта требуется определить погрешности положения и формы взаимодействующих поверхностей. Решение такой задачи представлено далее.
Данная задача является обратной по отношению к рассмотренной ранее, и методика её решения основывается на использовании ранее установленных зависимостей вида (14), (15), (16), (20). Эти зависимости применительно к данной постановке задачи могут быть приведены к общей форме вида
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
¿1 ‘А2 = I(ьк • Фо ), (23)
где значение / определяется по конкретной связи погрешностей ¿1 и А 2 контактирующих поверхностей с относительной площадью пятна контакта Фо.
Каждый ряд требуемых значений Фо1, Фо2,… при сочетании конкретных видов контактирующих поверхностей может быть представлен семейством гипербол вида (23), (рис. 3). По этим зависимостям гиперболического вида могут быть построены номограммы или составлены программы для работы в режиме диалога с ЭВМ. Номограммы следует рассматривать как средство малой механизации вычислительных работ при проектировании, а программы – как прикладные решения.
Рис. 3. Семейство гипербол
Поскольку величины раскрытия стыков А^ и А2 представляют собой допуски замыкающих звеньев размерных цепей, составленных в свою очередь, из раскрытий стыков контактирующих поверхностей, то
г -, т+п
А1 = Ы = Т.Ы Тг
1—1 т+п
г -I ///Т/7
^2 = [Та2= Т
7=1
Т7
(24)
где Гд^ – допуск исходного звена в первом направлении; £,7- – передаточное
отношение (в общем случае ^ = ^^ ) составляющих звеньев первого на-
правления; Г, – допуск /-го составляющего звена первого направления; Гд2 – допуск исходного звена второго направления; – передаточное
отношение составляющих звеньев второго направления; 2}’ – допуск у-го составляющего звена второго направления.
Допуски составляющих звеньев для каждого из направлений можно определить, используя способ равных допусков [5, 6]. Тогда:
Г. =м
гс т+п 5
1=1
Т К]
¡с – т+п. . (26)
дЫ
Для расчёта по вероятностному методу необходимо воспользоваться следующими формулами:
7/1+7? 0 А- 7 >
/777+77 0 № 4 •Г7?>
(27)
где / – коэффициент риска; – коэффициенты относительного рас-
сеяния соответственно для первого и второго направлений (результирующих раскрытий стыков А| и А2).
Допуски составляющих звеньев соответственно для раскрытий стыков А| и Д2) определяются по формулам:
1 K
h i 2 2 I KiA =1 у
Irn+n n, n, ‘J
Проверку равенств (26) и (27) и корректировку составляющих 7 и Tj■ целесообразно производить в режиме диалога с ЭВМ.
Список литературы
1. Грязев В.М., Ямников А.С. Размерные цепи с нормированным контактом поверхностей / «Фундаментальные и прикладные проблемы техники и технологии». Орел, ФГБОУ ВПО «Госуниверситет – УНПК», №6-3 (290) 2011, С. 12-17.
2. Васильев А.С., Грязев В.М., Ямников А.С. Функционально связанные сборочные размерные цепи, обеспечивающие нормированный контакт поверхностей / Сборка в машиностроении, приборостроении. Издательство «Машиностроение», № 5, 2012. С. 36-40.
3. Грязев В.М. Аналитическое определение величины контактного сближения плоских стыковых поверхностей / Известия ТулГУ. Технические науки. 2012. №8. С. 3-10.
4. Васильев А.С., Грязев В.М. Определение характеристик поверхностного слоя деталей, обработанных различными способами /«Фундаментальные и прикладные проблемы техники и технологии». Орел, ФГБОУ ВПО «Госуниверситет – УНПК», №2-5 (292), 2012. С. 3-6.
5. Детали и механизмы металлорежущих станков, Т.1 / Под редакцией Д.Н. Решетова. М.: Машиностроение, 1972. 664 с.
6. Решетов Д.Н., Портман В.Т. Точность металлорежущих станков. М.; Машиностроение, 1986. 336 с.
V.M. Griazev
THE METHODOLOGY OF DETERMINING THE CONTACT SPOT AREA FOR THE ERROR OF THE POSITION AND FORM OF THE CONTACT SURFACES
Given the analytical description of the dependences of the impact of the errors of the position and shape of the contact surfaces on the contour and the relative area of the contact spot of mating surfaces, as well as on security soot. The solution of the inverse problem definition of permissible errors of position and shape of the contacting surfaces with a given contact patch.
Key words: soot, the spot of contact, errors of form, position error.
Получено 20.11.12
Как найти площадь “пятна контакта” ролика (цилиндра) с плоскостью (касательной плоскостью)?
.
Ученик
(143),
на голосовании
4 года назад
Допустим у нас есть металлический вал (ролик, цилиндр), его ширина = 12 см, а внешний диаметр = 4 см. Данный идеально гладкий ролик горизонтально положили на идеально гладкую и ровную поверхность. Как найти площадь “пятна контакта” ролика с поверхностью?
Голосование за лучший ответ
Федор Новиков
Искусственный Интеллект
(313899)
4 года назад
Есть усилие, прижимающее этот ролик, есть упругость материала (давление, возникающее при продавливании на определенную глубину). Нужно найти равновесие между силой прижима и силой упругости.
AlexandEr Alex
Искусственный Интеллект
(126307)
4 года назад
Линия длиной 120 мм. Коль скоро все идеально гладкое и ровное.
&Ъ
Искусственный Интеллект
(148603)
4 года назад
–>0
.Ученик (143)
4 года назад
Ясно, что больше ноля)))) Но нужна конкретная формула площади))
&Ъ
Искусственный Интеллект
(148603)
ноль — в идеале и без сопромата
Pavel Rod
Гуру
(2632)
4 года назад
S=пиD^2/4
.Ученик (143)
4 года назад
Может S=π*D²/4*L?
Pavel Rod
Гуру
(2632)
ты же ищешь площадь, а не объем????
J3QQ4-H7H2V-2HCH4-M3HK8-6M8VW
Мудрец
(19476)
4 года назад
Начни с этого, а там будет видно…
https://ru.wikipedia.org/wiki/Механика_контактного_взаимодействия
.Ученик (143)
4 года назад
Благодарю

