Определение площади сложной фигуры с помощью теории вероятностей
Время на прочтение
3 мин
Количество просмотров 22K
Зачем определять площадь сложной фигуры?
Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте. Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника. Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.
В чём сложность нахождения площади?
Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?
Теория вероятностей, Ваш выход!
Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.
Суть метода
Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик. А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист. Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон.
Возвращаемся к нашей фигуре
Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.
Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования. Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что:
Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел. Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить. Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):
| 0 | 4 | 8 | 4 | 0 | 0 |
| 0 | 7 | 5 | 6 | 0 | 4 |
| 3 | 6 | 13 | 7 | 8 | 5 |
| 1 | 10 | 10 | 13 | 7 | 2 |
| 0 | 2 | 3 | 7 | 10 | 2 |
| 0 | 0 | 2 | 5 | 3 | 0 |
Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 157;
площадь фигуры – 209,33 кв. см.
И насколько это точно?
Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см. Для этого возьмём фигуру, площадь которой нам известна заранее. Например, такую:
Проставляем точки:
Результаты заносим в таблицу:
| 0 | 6 | 11 | 8 | 5 | 0 |
| 9 | 15 | 8 | 5 | 13 | 2 |
| 11 | 8 | 5 | 14 | 13 | 5 |
| 10 | 11 | 8 | 8 | 4 | 4 |
| 2 | 14 | 9 | 10 | 4 | 1 |
| 0 | 3 | 5 | 6 | 0 | 0 |
Рассчитываем площадь фигуры:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 237;
площадь фигуры – 316 кв. см.
Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.
|
Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы? Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так: И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм: Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример: S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим Ксарфакс 6 лет назад Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле: N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах. N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество. N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество. N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см². Марина Вологда 3 года назад Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач: Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника: Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика: Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник: Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2. Enot-Nina 3 года назад Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам: Бархатные лапки 3 года назад Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах. Ann Luka 6 лет назад Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток. Outline 3 года назад Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника: Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников: S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13. KritikSPb 3 года назад Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ. 127771 3 года назад Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где:
Теперь разберемся на примере, у нас есть такой пример: Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см. Бекки Шарп 3 года назад Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где
Вот такая фигура у нас – Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ? |
Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным
(Паскаль)
Добрый день, уважаемые гости и подписчики моего канала!
Вспомнил забавный случай, как около года назад я поспорил с дочкой, что найду площадь любого из представленных выше многоугольников за 30 секунд в одно действие, пока она будет вычислять её множеством действий, как учили в школе.
Выиграл. Дочь проспорила мороженое.
А раз вспомнил об этом, хочу рассказать и Вам, как просто в одно действие используя одну единственную формулу можно точно вычислить площадь многоугольника любой конфигурации и нет необходимости раскладывать фигуру на несколько простейших.
Но, для таких многоугольников есть одно важное условие: каждая вершина должна быть целочисленная, т.е. находиться именно в узле сетки.
Сетка – клеточная поверхность, на которой изображена фигура.
Узел – пересечение линий сетки.
Сетка может быть выполнена с любой единицей измерения, ведь площадь измеряется в квадратах выбранной единицы. Если ячейка 1х1 см., то это 1 кв.см., 1х1 м. – это 1 кв.м. и т.д.
Так вот, существует очень простая формула, которая связывает площадь любого многоугольника с количеством узлов сетки, находящихся на границах отрезков фигуры и внутри самой фигуры. Формулу вывел австрийский математик Георг Александр Пик в 1899 г., в честь которого и называется она формулой (теоремой) Пика:
где:
S – площадь многоугольника;
В – количество узлов внутри фигуры (шт.);
Г – количество узлов, расположенных в вершинах и на отрезках фигуры (шт).
Чтобы стало всё понятно, приведу пример со сложным многоугольником. Нам требуется найти площадь фигуры, представленной ниже:
Теперь, считаем узлы, расположенные внутри, на вершинах и на отрезках фигуры. Это будут значения В и Г, соответственно:
Получаем, что В=16, Г=7, теперь достаточно подставить значения в формулу и получаем: S=Г/2 + В – 1 = 7/2 + 16 -1 = 18,5 кв.ед.
Готово. Площадь равна 18,5 клеток. Вы можете всё перепроверить и будете приятно удивлены!
Плюсы в том, что такая формула легко запоминается и проста в применении! Минус конечно тоже есть, как я упоминал выше – формула не дает точного результата, если хотя бы одна из вершин многоугольника находится вне узла сетки (не целочисленная).
Моя дочь уже с успехом применяет эту формулу на занятиях в школе и быстро находит ответы, хотя некоторые учителя не одобряют такой подход и всё же склоняют к классической схеме: разделить многоугольник на элементарные фигуры, вычислить их площади, пользуясь стандартными формулами и сложив их, получить результат.
Но, всё же думаю, для скорости расчетов – формула полезна. Обязательно расскажите детям!
Очень надеюсь, что статья Вам понравилась! Удачи Вам и добра!
Предлагаю несколько публикаций, которые будут Вам интересны:
Метод быстрого счета. Как в старину перемножали многозначные числа без таблиц умножения? (крестьянский метод)
Какую площадь займет все население планеты, собравшись плечом к плечу? Удивитесь, но этот участок можно объехать за 1 час
Секрет строительного угольника Свенсона. Тригонометрическая зависимость шкал и какие 4 инструмента он объединяет?
Формулы площади
Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:
Что такое четырех угольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.
Четырехугольник – это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.
Формулы площади квадрата
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY .

Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле:
Найдем одну из сторон, к примеру, AB :
Подставим значения в формулу:
Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:
Формула вычисления площади
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними:
S = 1/2 * d1 * d2 * sin α
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Особые виды четырехугольников
Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:
- Параллелограмм
- Ромб
- Прямоугольник
- Квадрат
- Трапеция
- Дельтоид
- Контрпараллелограмм
Квадрат, прямоугольник и другие параллелограммы
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
- Площадь = сторона х сторона, или S = a 2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a 2 = 4 х 4 = 16 квадратных сантиметров.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .
Свойство диагоналей выпуклого четырехугольника
Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:
На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.
Свойства длин сторон четырехугольника
Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.
Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.
В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.
Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (<). Равенство достигается только в случае, если четырехугольник является “вырожденным”, то есть три его точки лежат на одной прямой. То есть эта ситуация не попадает под классическое определение четырехугольника.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

используем найденное значение для расчета площади:
Четырехугольник и окружность
Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).
Главное свойство описанного четырехугольника:
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.
Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)
Главное свойство вписанного четырехугольника:
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника , а φ – любой из четырёх углов между ними (рис. 1).
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
КГУ ЧЕРНОРЕЦКАЯ СОШ № 1
ПАВЛОДАРСКАЯ ОБЛАСТЬ
ПАВЛОДАРСКИЙ РАЙОН
СЕЛО ЧЕРНОРЕЦК
ТЕМІРБУЛАТ НАЗЕРКЕ
8 КЛАСС
НАХОЖДЕНИЕ ПЛОЩАДЕЙ НЕСТАНДАРТНЫХ ФИГУР
НАПРАВЛЕНИЕ: Математическое моделирование экономических и социальных процессов
СЕКЦИЯ: Прикладная математика
Руководитель проекта: учитель математики, педагог-мастер
Середкин В. П.
Научный консультант: к.п.н. ассоциированный профессор (доцент) факультета Computer Science Торайгыров университета
Даниярова Ж.К.
Павлодар, 2022 г.
ОГЛАВЛЕНИЕ
ЭССЕ
АННОТАЦИЯ
РЕЦЕНЗИЯ
ВВЕДЕНИЕ
ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУРЫ НА КЛЕТЧАТОЙ БУМАГЕ.
ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ ВЫПУКЛОГО МНОГОУГОЛЬНИКА.
РАЗБИЕНИЕ.
ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.
ФОРМУЛА ПИКА.
ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕВЫПУКЛОГО МНОГОУГОЛЬНИКА.
ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.
ФОРМУЛА ПИКА.
МЕТОД МОНТЕ-КАРЛО И ПЛОЩАДИ ФИГУР
СРАВНИТЕЛЬНЫЙ АНАЛИЗ СПОСОБОВ НАХОЖДЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ.
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ЭССЕ
В своей работе я рассматриваю вопрос нахождения площадей нестандартных фигур. Все мы знаем определение площади. Площадь указывает размер плоскости, которую занимает фигура. Как мы можем ее найти? Для этого нам нужно знать линейные размеры фигуры и использование геометрические формулы для нахождения площадей. Как определить площадь фигуры неопределенной формы? Для этого можно использовать метод дополнения и разбиения, а можно воспользоваться основной формулой теории вероятности.
Способ разбиение заключается в том, что многоугольник разбивается на прямоугольники и прямоугольные прямоугольники. После нахождения площадей полученных прямоугольников и треугольников, площадь искомого многоугольника находиться путем сложения всех полученных площадей. Способ дополнения основывается на дополнении многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Формула Пика позволяет найти площадь фигуры на клетчатой бумаге. Любая фигура изображенная на с листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника.
Так же площадь многоугольника можно найти, используя основную формулу теории вероятности: вероятность равновероятностного события равна отношению положительных исходов к общему числу исходов

Эта формула легла в основу метода Монте-Карло.
Суть метода Монте-Карло в том, что выбирается некоторая плоскость с известной площадью и на нее переноситься фигура нестандартной формы. Далее на эту плоскость вбрасывается некоторое количество точек и выясняется, сколько точек попало на искомую площадь. Эти данные позволяют воспользоваться формулой вероятности для вычисления искомой площади.
Я думаю что метод Монте-Карло более легкий и удобный ,он находит приближенную площадь. В школьном курсе математики я использую метод Монте-Карло , он позволяет более точно вычислять площадь фигур , только в тех случаях , когда будет задействовано больше количество точек.
АННОТАЦИЯ
В школьном курсе математики мы в основном имеем дело с многоугольниками. С проблемой вычисления площади фигур я столкнулась при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которые мы не рассматривали на уроках математики. При изучении математик до 6 класса мы знакомимся только с формулами для вычисления площади квадрата и прямоугольника. Между тем, на практике часто возникает необходимость найти площадь фигуры неправильной формы. Например, необходимость определить площадь территории по плану или карте. Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников.
Гипотеза: площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.
Цель работы: исследовать различные способы вычисления площадей фигур.
Задачи исследования:
1. Изучить литературу по исследуемой теме;
2. Отобрать интересную и понятную информацию для исследования;
3. Найти способы вычисления площади не стандартных фигур.
Объектом исследования являются методы измерения площади фигур
произвольной формы:
1) способы нахождения площадей;
2) Метод Монте-Карло;
Предметом исследования является площадь фигур произвольной формы.
РЕЦЕНЗИЯ

ВВЕДЕНИЕ
В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д. Необходимость в понятии «площадь» возникла из жизненных потребностей.
В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе. Позже возникла потребность в измерении и сравнении разнообразных «фигур», например земельных участков. Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.
Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади. Вавилоняне, так же, как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.п. Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.
Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.
СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУРЫ НА КЛЕТЧАТОЙ БУМАГЕ.
При изучении вычисления площадей многоугольников на клетчатой бумаге я заметила, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.

Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления. [1, с.36]
ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ ВЫПУКЛОГО МНОГОУГОЛЬНИКА.
РАЗБИЕНИЕ.
Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. Тогда площадь фигуры можно сосчитать по формуле:
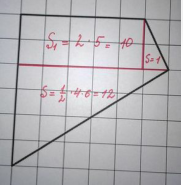

ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.
Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:
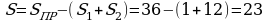
ФОРМУЛА ПИКА.
Любая фигура, изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так
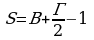
где В – количество внутренних узлов, а Г – количество узлов на границе многоугольника. Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге. Используя рисунок В= 17, Г = 14, получаем


Вычисляя площадь выпуклого многоугольника тремя способами, я получила один и тот же результат.
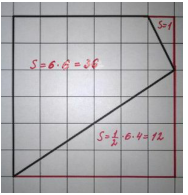
ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕВЫПУКЛОГО МНОГОУГОЛЬНИКА.
Способ разбиения не подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.
Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры
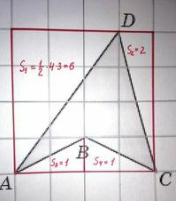
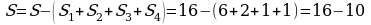
ФОРМУЛА ПИКА.
При подсчете внутренних узлов многоугольника и узлов, лежащих на границе, получим, что В = 5; Г = 4;
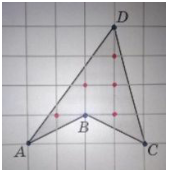
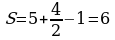
И опять я получила один и тот же результат.
Вычисление площади кольца по формуле Пика.
А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.
Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.

Вычислим площадь кольца с помощью формулы Пика: В=32, Г=8,
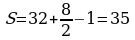
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.
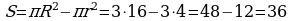
Округлим теперь π до десятых:
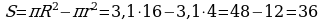
А если округлить число π до сотых, то получим:

Сравнив результаты, можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников. [2, с.17], [4]
МЕТОД МОНТЕ-КАРЛО И ПЛОЩАДИ ФИГУР
Рассмотрим достаточно интересный метод, который применятся в программировании, алгоритмизации и математике.
Метод основан на применении теории вероятности к алгоритмическим процессам нахождения приближенных значений. Значение отыскиваются путем сравнения результатов равновероятностных событий на два множества, одно из которых полностью включает другое. Полностью включенное множество как раз объявляется как требуемое к отысканию. Более крупное множество, должно быть заведомо с известным значением.
Основная формула теории вероятности: вероятность равновероятного события равна отношению положительных исходов к общему числу исходов
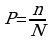
М
Возьмем множество А и множество В которое полностью принадлежит множеству А графически это можно представить в следующем виде рисунок 3.
Исходами в методе Монте-Карло являются выпадения точек в случайных координатах в общее множество часть из которых попадет и во включенное подмножество в формуле вероятности для метода Монте-Карло 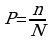

Как это может помочь при решении задач с площадями? Нам будет необходим следующий постулат – Отношение числа исходов с внутренним множеством которое требуется найти на число исходом с общим множеством приблизительно равно отношению сравниваемых параметром этих множеств в нашем примере отношение числа точек в указанных множествах будет примерно таким же, как и отношение площадей.
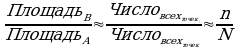
Далее по этой пропорции выражаем площадь В
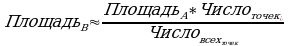
В эту формулу можно будет подставлять числа для расчета.
Р
Форма листа клена очень сложная рисунок 5. Вычислить площадь трудно. Но используя метод Монте-Карло данную площадь найти легко.
С
Так как мы ищем площадь кленового листа то это будет искомая площадь В, а общую область нужно выбрать больше с известной площадью например лист А4 рисунок 6. Теперь сформируем общее множество и получим объединенное выражение.

Используя метод Монте-Карло для нашего изображения. Прокинем на изображение 1000 точек. Из этого числа на лист клена выпало 480 точек. Площадь листа А4 равна 623,7 см2. Тогда площадь листа мы сможем вычислить по формуле
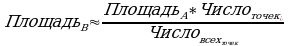

Ниже приводится сравнительная таблица эксперементальных опытов представленной задачи. На основании результатов исследования можно сделать вывод: чем большее количество точек мы будем вбрасывать на плоскость тем точнее будет получаться результат нахождения площади.
|
СРАВНИТЕЛЬНАЯ ТАБЛИЦА РАСЧЕТОВ |
||||
|
№ опыта |
N |
n |
S(A), кв. см. |
S(B), кв. см. |
|
1 |
1000 |
480 |
623,7 |
299,38 |
|
2 |
1500 |
700 |
623,7 |
291,06 |
|
3 |
2000 |
950 |
623,7 |
296,26 |
|
4 |
2500 |
1200 |
623,7 |
299,38 |
|
5 |
3000 |
1400 |
623,7 |
291,06 |
|
6 |
3500 |
1650 |
623,7 |
294,03 |
|
7 |
4000 |
1900 |
623,7 |
296,26 |
|
8 |
4500 |
2150 |
623,7 |
297,99 |
|
9 |
5000 |
2400 |
623,7 |
299,38 |
|
10 |
5500 |
2650 |
623,7 |
300,51 |
Р
Задача: По аэрофотосъемки некоторой области океана с известной площадью найти приблизительно площадь острова на фото. Известно, что территория на снимке занимает площадь 27 кв.км рисунок 8.
Площадь острова из-за неровных краев и сложной не прямоугольной формы нам неизвестна как же можно, найти, площадь острова не зная функции кривых периметров. В данном случае найти площадь острова нам поможет метод Монте-Карло.
П
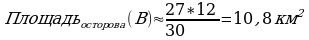
В сравнительной таблице расчетов приводятся результаты экспериментальных опытов. И как в предыдущей задаче с кленовым листом мы приходим к выводу, что при увеличении количества вбрасываемых точек результаты становятся более точными
|
СРАВНИТЕЛЬНАЯ ТАБЛИЦА РАСЧЕТОВ |
||||
|
№ опыта |
N |
n |
S(A) кв.км. |
S(B)кв. км. |
|
1 |
30 |
12 |
27 |
10,8 |
|
2 |
40 |
17 |
27 |
11,475 |
|
3 |
50 |
27 |
27 |
14,58 |
|
4 |
60 |
32 |
27 |
14,4 |
|
5 |
70 |
40 |
27 |
15,428571 |
|
6 |
80 |
51 |
27 |
17,2125 |
|
7 |
90 |
64 |
27 |
19,2 |
|
8 |
100 |
72 |
27 |
19,44 |
|
9 |
110 |
81 |
27 |
19,881818 |
|
10 |
120 |
91 |
27 |
20,475 |
СРАВНИТЕЛЬНЫЙ АНАЛИЗ СПОСОБОВ НАХОЖДЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ.
Разбиение. Этот способ прост в подсчёте площадей фигур, которые разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. К ним относятся выпуклые многоугольники. К минусам можно отнести то, что в использовании этого способа приходится производить множество действий, а так же невозможность подсчёта площади фигур, которые не разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.
Дополнение до прямоугольника. Этот способ так же прост в подсчёте при вычислении площади при небольшом количестве фигур, площадь которых необходимо отнять. Минусы этого способа – сложность подсчёта площади многоугольников необычной формы, большое количество фигур, площадь которых необходимо отнять, а также невозможность подсчёта площади фигур, не относящихся к многоугольникам.
Формула Пика. К плюсам я отнесла то, что легко вычисляется площадь многоугольника с необычной формой, в отличие от предыдущих способов, краткость формулы, а также возможность вычисления приближенного значения площади местности по карте, представив ее в виде многоугольника, перенеся ее на клетку. Минусами этого способа считаю сложность вычисления площади фигуры с большим количеством узлов, а так же, если в фигуре есть «спорные» узлы (узлы, лежащие близко к стороне многоугольника). Вычисляя площадь фигур, не относящихся к многоугольникам, результат получается не точным.
Метод Монте-Карло. Позволяет более точно вычислять площадь фигур, только в тех случаях, когда будет задействовано большое количество точек.
ЗАКЛЮЧЕНИЕ
Изучив различные источники, выяснилось, что существует различные способы вычисления фигур по клеткам, но для меня были интересны и понятны три: разбиение, дополнение до прямоугольника и вычисления по формуле Пика. Также интересным способом нахождения площади произвольной фигуры является метод Монте-Карло.
Моя гипотеза – о том, что если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми, частично подтвердилась. Рассмотрев все три способа, я пришла к выводу, что не для всякой фигуры можно приметить каждый из них. У каждого из них есть свои плюсы и минусы.
Все три способа можно применить только для выпуклых многоугольников, перенеся их на клетчатую поверхность.
Формула Пика интересна своей простотой. И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.
Как оказалось метод Монте-Карло является пригодным для приближенного нахождения площадей фигур сложной формы.
СПИСОК ЛИТЕРАТУРЫ
1. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
2. История математики с древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича., издательство Наука., М., 1970г
3. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.:
Чистые пруды, 2009.



























 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.





























