Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
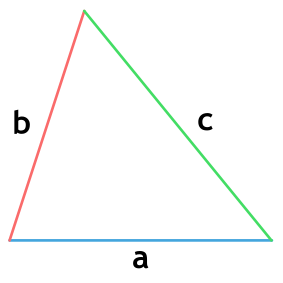
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

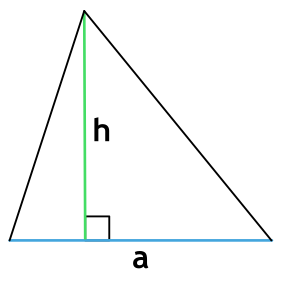
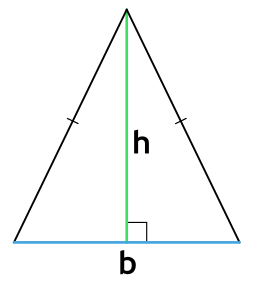
Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

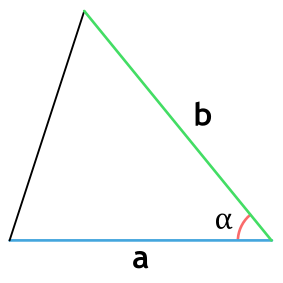
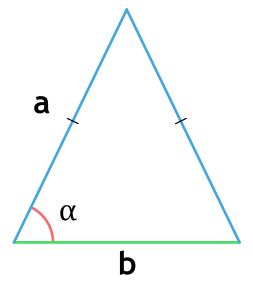
Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

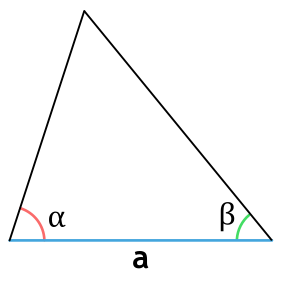
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

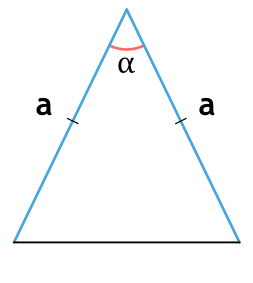
Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

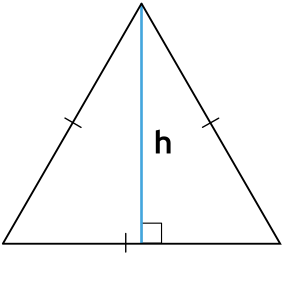
Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
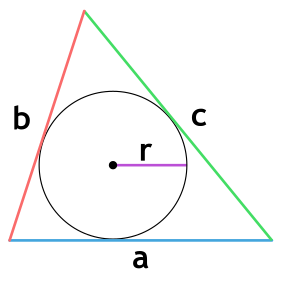
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

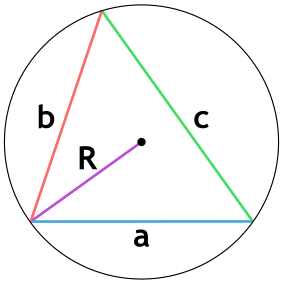
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
32 434
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
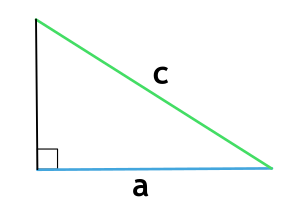
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
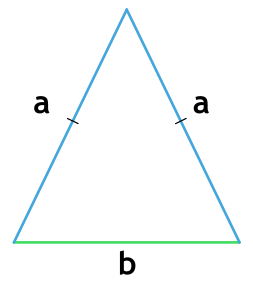
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
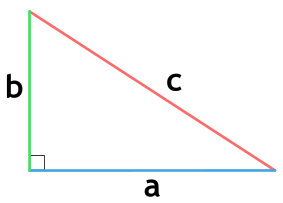
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
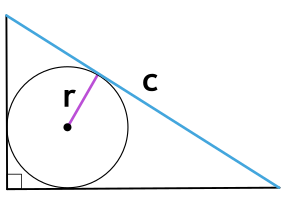
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
( 32 оценки, среднее 4.44 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
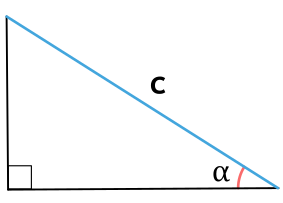
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
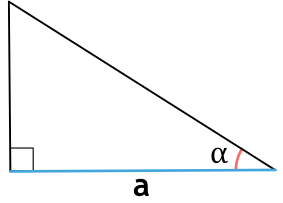
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Содержание:
- Формула
- Примеры вычисления площади равнобедренного треугольника
Формула
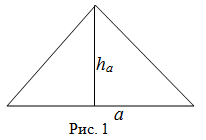
Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:
$$mathrm{S}_{Delta}=frac{1}{2} a h_{a}$$
Напомним, что треугольник называется равнобедренным, если его две стороны равны. Равные стороны
называются боковыми сторонами рассматриваемого треугольника, а третья сторона – основанием.
Примеры вычисления площади равнобедренного треугольника
Пример
Задание. Найти площадь равнобедренного треугольника
$ABC$, если известно, что его основание равно
4 м, а высота, проведенная к этому основанию – 6 м.
Решение. Искомая площадь равна произведению высоты на основание, деленному на два:
$mathrm{S}_{Delta A B C}=frac{4 cdot 6}{2}=frac{24}{2}=12$ (м2)
Ответ. $mathrm{S}_{Delta A B C}=12$ (м2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
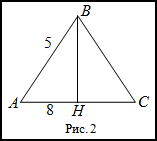
Задание. Найти площадь равнобедренного треугольника, боковая сторона которого равна 5 см, а основание 8 см.
Решение. Сделаем чертеж (рис. 2).
Проведем высоту $BH$. По свойству равнобедренного
треугольника она является и медианой. Поэтому
$A H=H C=frac{8}{2}=4$ (см)
Рассмотрим прямоугольный треугольник $ABH$. По теореме
Пифагора найдем его катет $BH$ :
$B H=sqrt{A B^{2}-A H^{2}}=sqrt{5^{2}-4^{2}}=sqrt{25-16}=sqrt{9}=3$ (cм)
А тогда искомая площадь
$mathrm{S}_{Delta A B C}=frac{1}{2} A C cdot B H=frac{8 cdot 3}{2}=4 cdot 3=12$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=12$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Площадь равнобедренного треугольника с прямым углом составляет 16 см кв.
Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего
прямой угол. В этом случае его площадь будет представлять собой ½ длины
его катета, возведенную в квадратную степень. Это значит, что квадрат
катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.
Для того чтобы найти длину катета, нужно извлечь корень квадратный из
числа 32:
х = 4*√2 см.
Теперь можно высчитать длину гипотенузы, которая будет равна:
х / sin45 = 8 см.
Ответ: Длина гипотенузы равна 8 см.
Имеется равнобедренный треугольник площадью 192 см кв. Его основание
составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на
высоту:
S=АС*ВН/2
Из этой формулы можно выразить ВН:
ВН=2S/АС=2*192/32=12 см.
Известно, что в равнобедренном треугольнике две стороны равны:
АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен
сумме длин его сторон:
Р=2АВ+АС=40+32=72 см.
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Длина гипотенузы равнобедренного треугольника, имеющего прямой угол,
составляет 12 см. Как найти площадь данного треугольника?
Обозначим буквой х катет имеющегося треугольника. Тогда по теореме
Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
x²=72, x=√72
Зная длину катета равнобедренного треугольника, можно найти его площадь
(S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Дан равнобедренный треугольник, угол в основании которого составляет 25
градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный
треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно
отношение оснований этих двух треугольных фигур?
Разберемся с первым из треугольников. Так как он является равнобедренным,
то оба угла при его основании будут равны. Зная о том, что сумма всех
углов треугольника равна 180 градусом, мы можем найти третий угол
треугольника, находящийся при его вершине:
180-25-25=130 градусов.
Переходим ко второму треугольнику. Известно, что угол при его вершине
равен 230 градусом. Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
(180-130)/2=25 градусов.
Очевидно, что треугольники являются подобными на основании равенства
углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат
коэффициента подобия будет равен отношению площадей треугольников:
49/16=kˆ2
Отсюда выражаем k:
k=7/4
Коэффициент подобия представляет собой отношение основания первой подобной
треугольной фигуры ко второй. Это значит, что:
С/c=k = 7/4
Ответ: Отношение оснований двух треугольников равно 7/4.
Чему равна площадь равнобедренного треугольника с прямым углом при условии,
что длина его гипотенузы составляет с?
Площадь (S) треугольника с прямым углом составляет ½ часть произведения
его катетов. Принимая во внимание тот факт, что треугольник является
равнобедренным, можно утверждать, что длины его катетов равны. Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
S=½x*x=½x²
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
с²=х²+х²=2x²
x²=½c²
Подставим в формулу площади получившееся равенство:
S=½*½с²=¼с² см.кв.
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Как можно рассчитать площадь равнобедренного треугольника, если длина его
высоты и основания – величины известные?
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам
произведения длины его основания (с) и высоты (h):
S = ½ c*h
Как найти площадь равнобедренного треугольника?
Площадь каждого треугольника, в том числе и равнобедренного,
рассчитывается как половина, взятая от произведения длины высоты
треугольника и его основания. Формула имеет следующий вид:
S=1/2 *a*h
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой
по той причине, что треугольник равнобедренный. В результате образовался
треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один
из катетов треугольника равен h, а второй рассчитывается как а/2:
150/2=75 см.
Теперь можно рассчитать длину второго катета (на основании теоремы
Пифагора):
h=√85²-75²=√7225-5625=√1600=40 см.
Когда все необходимые для расчета площади треугольника величины известны,
можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Как можно найти площадь треугольника при условии, что он является
равнобедренным, и его периметр равен 100 см, а основание – 48 см?
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его
периметра длину основания и разделив полученное число на 2:
(100-48):2=26 см.
Тогда площадь равнобедренного треугольника с заданными параметрами будет
равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.
Чему равна площадь равнобедренного треугольника, длины сторон которого
составляют 10 см и 12 см (сумма длин его катетов)?
К основанию равнобедренного треугольника проведем высоту, делящую его на
две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и
катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10
см.
В случае с прямоугольным треугольником может быть применима теорема
Пифагора, которая поможет найти катет, являющийся высотой треугольника:
h² = 10² – 6² = 64 см
Избавимся от квадратов:
h = 8 см.
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Как рассчитать площадь равнобедренного треугольника, если известно о том,
что длина его гипотенузы составляет 44 см?
Введем условные обозначения, согласно которым х – это длина одного из
катетов равнобедренного треугольника. В этом случае длина второго катета
тоже будет равна х. Зная длину гипотенузы, можно записать формулу теоремы
Пифагора для имеющегося треугольника:
х²+ х² = 44²
2х² = 1936
Отсюда можем найти значение х:
x=√968
Найдя длину катета равнобедренного треугольника, можно вычислить его
площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Каким образом возможно высчитать площадь равнобедренного треугольника через
стороны и длину его основания?
Располагая сведениями о длине основания (b) и стороны (a) треугольной
фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С
этой целью следует пользоваться приведенной ниже формулой:
S = b/4×√ 4× a²-b².
Возможно ли определить площадь равнобедренного треугольника через его
боковые стороны и образованный ими угол?
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной
длины и размере угла (α), который образован этими катетами, позволит
определить площадь этой фигуры. В этом поможет следующая формула:
S = 1/2a2 * sin(α).
Как можно высчитать площадь равнобедренного треугольника при условии, что
известна длина его основания и угол?
Для расчета площади треугольной фигуры с катетами равной длины, при
условии, что известна их длина (а), основание (b) и угол, который
образован основанием и одним из катетов(α), используется следующая
формула:
S = ½ * a * b * sin(α)
Длина основания равнобедренного треугольника превышает длину его боковой
стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно
высчитать длину основания данного равнобедренного треугольника?
Примем неизвестную длину основания равнобедренного треугольника за х. В
данном случае длина каждой из боковых сторон, которые в равнобедренном
треугольнике равны, будет составлять (х-3). Известно, что периметр (Р)
треугольника равен 30 см. Тогда:
Р = 3х-6 = 30 см.
Отсюда можно вывести х:
х = (30+6)/3 = 12 см.
Ответ: Длина основания равна 12 см.
Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина
основания данной фигуры превышает длину его боковой стороны на 15 см. Как
найти основание равнобедренного треугольника в этом случае?
Примем х за длину основания равнобедренного треугольника. Тогда длина его
боковой стороны будет составлять (х-15). Высота, проведенная в
треугольнике с прямым углом, также представляет собой его медиану, которая
делит его на две равных треугольных фигуры. Следует рассмотреть одну из
образовавшихся треугольных фигур. Для начала вычислим ее основания,
используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
225-x²-30x+225-0,25x²
0=0,75x²-30x
x(0,75x-30)=0
x¹=0 см.
x=40 см.
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см.
Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
По какой формуле можно высчитать площадь равнобедренного треугольника?
Для ответа на поставленный вопрос следует провести высоту из вершины того
угла равнобедренного треугольника, который является противоположным его
основанию. После этого длину проведенной высоты (а) нужно умножить на
длину основания фигуры (b), а затем разделить полученное значение на два.
Формула расчета площади треугольной фигуры, которая является
равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
В равнобедренном треугольнике к его основанию проведена высота, длина
которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как
рассчитать длину боковой стороны этого равнобедренного треугольника?
Вычислим половину длины основания данного равнобедренного треугольника:
3,2/2 = 1,6 см.
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см
и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить,
используя теорему Пифагора:
с²=а²+в²
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
с=√4=2 см.
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Один из углов равнобедренного треугольника является тупым. Одна сторона
данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание
треугольника с двумя равными сторонами?
Известно, что углы, расположенные у основания равнобедренного
треугольника, всегда являются острыми, иначе сумма всех трех углов
превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что
тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена
напротив тупого угла, имеет большую длину, чем сторона, лежащая против
острого угла треугольника. Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны. По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в
нем, составляет 21 см. Чему равно основание треугольника с указанными
параметрами?
Для решения данной задачи следует воспользоваться теоремой Пифагора:
с²=а²+в²
Отсюда можно выразить квадрат длины неизвестной стороны, который будет
равен разности квадратов известной стороны и высоты:
29²-21² = 400.
Для того чтобы узнать длину основания равнобедренного треугольника, нужно
извлечь корень квадратный из числа 400, а затем умножить полученное число
на 2:
√400*2 = 20*2 = 40 см.
Ответ: Длина основания равнобедренного треугольника равна 40 см.
Читать дальше: как найти площадь равностороннего треугольника.
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?