Площадь квадрата можно найти с помощью двух основных формул:
1) Через сторону.
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат – это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b – стороны прямоугольника.
В случае с квадратом a = b.
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата – катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b – катеты, c – гипотенуза.
В нашем случае a = b, а гипотенуза – это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².
Квадрат – это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).
- Формула вычисления площади
-
Примеры задач
Формула вычисления площади
1. По длине стороны:
Площадь квадрата (S) равняется квадрату длины его стороны:
S = a2
Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:
S = a*b
А т.к. все стороны квадрата равны, то вместо стороны b мы снова подставляем в формулу сторону a, т.е. S = a*a = a2.
2. По по длине диагонали
Площадь квадрата равняется половине квадрата длины его диагонали:
S = d2/2
Соотношение стороны и диагонали квадрата: d=a√2.
Примеры задач
Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.
Решение:
Используем формулу по длине стороны, т.е. S = 72 = 49 см2.
Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.
Решение 1:
Воспользуемся второй формулой (по длине диагонали): S = 42/2 = 8 см2.
Решение 2:
Мы можем выразить длину стороны через диагональ: a = 4/√2. И тогда, используя первую формулу, S = (4/√2)2 = 8 см2.
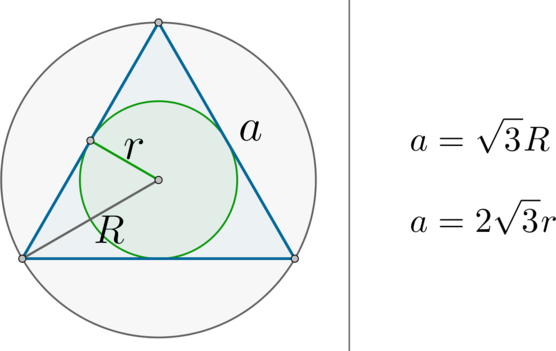
Факт 1.
(bullet) Площадь правильного треугольника равна [{large{S=dfrac{sqrt3a^2}4qquad qquad S=dfrac{3sqrt3R^2}4qquadqquad
S=3sqrt3r^2}}] где (a) – его сторона, (R) и (r) – радиусы описанной и вписанной окружностей соответственно.
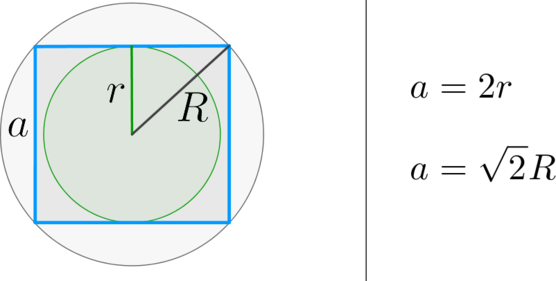
Факт 2.
(bullet) Площадь правильного четырехугольника (квадрата) равна [{large{S=a^2qquad qquad S=2R^2qquadqquad
S=4r^2}}] где (a) – его сторона, (R) и (r) – радиусы описанной и вписанной окружностей соответственно.
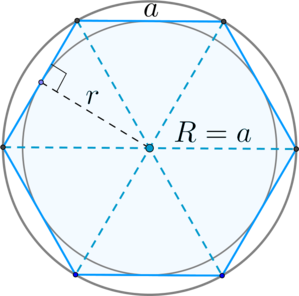
Факт 3.
(bullet) Правильный шестиугольник – шестиугольник, у которого все стороны равны и все углы равны.
(bullet) Свойства:
1. Все углы равны по (120^circ).
2. Сторона (a) равна радиусу (R) описанной окружности: [a=R] 3. Радиус (r) вписанной окружности равен [r=dfrac{sqrt3}2a] 4. Большие диагонали делят его на 6 равносторонних треугольников.
5. Большая диагональ равна (2a).
6. Центры вписанной и описанной окружностей совпадают.
(bullet) Площадь правильного шестиугольника равна [{large{S=dfrac{3sqrt3a^2}2qquadqquad
S=2sqrt3r^2}}] где (a) – его сторона, (R) и (r) – радиусы описанной и вписанной окружностей соответственно.

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Квадрат, свойства и формулы, площадь и периметр.
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат (понятие, определение), диагональ квадрата
Свойства квадрата
Формулы квадрата. Площадь квадрата. Периметр квадрата
Квадрат (понятие, определение), диагональ квадрата:
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат – это четырехугольник, имеющий равные стороны и углы.
Рис. 1. Квадрат
Все углы квадрата прямые. Каждый из них прямой и равен 90°.
Таким образом, все квадраты отличаются друг от друга только длиной стороны.
Рис. 2. Квадрат и диагонали квадрата
Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.
Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника.
Квадрат – это равносторонний прямоугольник.
Квадрат – это ромб с прямыми углами.
Свойства квадрата:
1. Длины всех сторон равны.
Рис. 3. Квадрат
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны.
Рис. 4. Квадрат
AB||CD, BC||AD
3. Все углы квадрата прямые. Каждый из них равен 90°.
Рис. 5. Квадрат
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусам.
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
5. Диагонали квадрата равны между собой.
Рис. 6. Квадрат
AC = BD
6. Диагонали квадрата взаимно перпендикулярны.
Рис. 7. Квадрат
AC ┴ BD
7. Диагонали квадрата точкой пересечения делятся пополам.
Рис. 8. Квадрат
BO = OD = AO = OC
8. Угол между диагональю и стороной квадрата равен 45 градусам.
Рис. 9. Квадрат
∠BCA = ∠ACD = ∠DAC = ∠CAB = 45°
9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.
Рис. 10. Квадрат
∠ABD = ∠DBC = ∠BCA = ∠ACD = ∠CDB = ∠BDA = ∠DAC = ∠CAB = 45°
10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.
Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника.
Рис. 11. Квадрат
△ABD = △CBD = △ABC = △ACD,
△AOB = △BOC = △COD = △AOD
11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.
Рис. 12. Квадрат
Формулы квадрата. Площадь квадрата. Периметр квадрата:
Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.
Формула диагонали квадрата:
,
,

,
.
Формула радиуса вписанной окружности квадрата:
Радиус вписанной окружности квадрата равен половине его стороны.

Формула радиуса описанной окружности квадрата:

Формула периметра квадрата:
,
,
.
Формула площади квадрата:
,


,
.
Квадрат
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
3 893