Как найти площадь равностороннего многоугольника - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Правильный многоугольник представляет собой двумерную выпуклую фигуру, у которой все стороны и углы равны. Площадь некоторых многоугольников, таких как треугольников или четырехугольников, можно найти по простым формулам, но если у многоугольника больше четырех сторон, воспользуйтесь формулой, в которую входит апофема и периметр фигуры.

1

Вычислите периметр. Периметр равен сумме всех сторон многоугольника. Если многоугольник правильный, периметр равен произведению одной стороны на число сторон «n».^[1]
2
Найдите апофему. Апофема — это перпендикуляр, опущенный из центра многоугольника на любую из его сторон. Найти апофему немного сложнее, чем периметр.
- Формула для вычисления апофемы: а = s/(2tg(180/n)), где «s» — сторона, «n» — число сторон.
3

Запишите формулу для вычисления площади. Площадь любого правильного многоугольника вычисляется по формуле: S = (a * p)/2, где «a» — апофема, «p» — периметр.
4
Подставьте значения «а» и «р» в формулу, чтобы вычислить площадь. Для примера рассмотрим шестиугольник (n = 6), сторона которого равна 10 см (s = 10).
- Периметр: р = n * s = 6 * 10 = 60.
- Вычислите апофему. а = s/(2tg(180/n)) = 10/(2tg(180/6)) = 10/1,1547 = 8,66.
- Площадь многоугольника: S = (a * p)/2 = (8,66 * 60)/2 = 259,8 см².
- Обратите внимание, что (8,66 * 60)/2 = (8,66/2) * 60 = 8,66 * (60/2), то есть на 2 можно сначала разделить апофему или периметр, а не произведение апофемы и периметра. При этом вы получите один и тот же результат.
Реклама

1

Представьте правильный многоугольник как совокупность нескольких треугольников. Каждая сторона многоугольника представляет собой основание треугольника; таким образом, число треугольников равно числу сторон многоугольников. Все треугольники равны, то есть равны их стороны и высоты.^[2]
2

Вспомните формулу для вычисления площади треугольника. S = 1/2bh, где «b» — основание треугольника (которое совпадает со стороной многоугольника), «h» — высота треугольника (которая совпадает с апофемой правильного многоугольника).^[3]
3

Обратите внимание на сходство формул. Формула для вычисления площади правильного многоугольника S = 1/2аp, где «а» — сторона многоугольника, «р» — периметр многоугольника. Периметр равен стороне, умноженной на число сторон («n»); в правильном многоугольнике «n» равно числу треугольников, составляющих многоугольник. Таким образом, формула для вычисления площади многоугольника представляет собой формулу для вычисления площади треугольника, умноженную на количество треугольников в многоугольнике.^[4]

Реклама

Советы

Если правильный многоугольник разделен на треугольники, а площадь одного треугольника дана, вычислять апофему не нужно. Просто умножьте площадь одного треугольника на количество сторон многоугольника.

Об этой статье

Эту страницу просматривали 27 450 раз.

Была ли эта статья полезной?

Источник

Каким способом считать:

Через тангенс

Через радиус вписанной окружности

Укажите размеры:

Количество сторон

Длина одной стороны

Площадь:

Решение:

Ссылка на страницу с результатом:

# Теория

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Правильный многоугольник так же называют правильным n-угольником, где n – это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.

Около любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

Формулы площади правильного многоугольника

S = dfrac {n cdot a^2}{4 cdot tg lparen dfrac{360degree}{2n} rparen}

S = dfrac {n cdot a^2}{4 cdot tg lparen dfrac{180degree}{n} rparen}

S – площадь правильного многоугольника
n – количество сторон
a – длина стороны
tg – тангенс

Площадь правильного многоугольника через радиус вписанной окружности

S = p cdot r

S = dfrac{1}{2} cdot n cdot a cdot r

S – площадь правильного многоугольника
p – полупериметр правильного многоугольника
r – радиус вписанной окружности правильного многоугольника
n – количество сторон
a – сторона правильного многоугольника

p = dfrac{n cdot a}{2}

Войдите чтобы писать комментарии

Источник

Правильный многоугольник
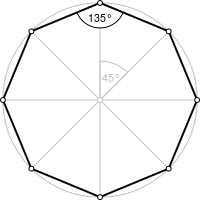Правильный восьмиугольник
Тип	Многоугольник
Символ Шлефли
Вид симметрии	Диэдрическая группа ${displaystyle (mathrm {D} _{5})}$
Площадь	${displaystyle S={frac {n}{4}} a^{2}operatorname {ctg} {frac {pi }{n}}}$
Внутренний угол	${displaystyle (n-2)*180^{circ }}$
Свойства
выпуклый, вписанный, равносторонний, равноугольный^[en], изотоксальный
Медиафайлы на Викискладе

Пра́вильный многоуго́льник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Связанные определения[править | править код]

Центром правильного многоугольника называется его центр масс, совпадающий с центрами его вписанной и описанной окружностей.

Свойства[править | править код]

Координаты[править | править код]

Пусть $x_{C}$ и $y_{C}$ — координаты центра, а — радиус описанной вокруг правильного многоугольника окружности, ${phi }_{0}$ — угловая координата первой вершины относительно центра, тогда декартовы координаты вершин правильного n-угольника определяются формулами:

$x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)$

$y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)$

где принимает значения от до n-1 .

Размеры[править | править код]

Правильный многоугольник, вписанный и описанный около окружности

Пусть — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен

$r=Rcos {frac {pi }{n}}$

а длина стороны многоугольника равна

$a=2Rsin {frac {pi }{n}}=2r{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь[править | править код]

Площадь правильного многоугольника с числом сторон и длиной стороны составляет:

$S={frac {n}{4}} a^{2}{mathop {{mathrm {}}}},operatorname {ctg}{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон , вписанного в окружность радиуса , составляет:

$S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}$

Площадь правильного многоугольника с числом сторон , описанного вокруг окружности радиуса , составляет:

$S=nr^{2}{mathop {{mathrm {tg}}}},{frac {pi }{n}}$

Площадь правильного многоугольника с числом сторон равна

${displaystyle S={frac {nra}{2}}={frac {1}{2}}Pr}$

где — радиус вписанной окружности многоугольника, — длина его стороны, а – его периметр.

Периметр[править | править код]

Если нужно вычислить длину стороны a_n правильного n-угольника, вписанного в окружность, зная длину окружности можно вычислить длину одной стороны многоугольника:

— длина стороны правильного n-угольника.

${displaystyle a_{n}=sin {Big (}{frac {pi }{n}}{Big )}cdot {frac {L}{pi }}}$

Периметр $P_{n}$ равен

$P_{n}=a_{n}cdot n$

где — число сторон многоугольника.

Свойства диагоналей правильных многоугольников[править | править код]

Максимальное количество диагоналей правильного -угольника, пересекающихся в одной точке, не являющейся его вершиной или центром, равно:

Существуют лишь три исключения: данное число равно

в треугольнике,

в шестиугольнике и

в двенадцатиугольнике.^[3].

При чётном

в центре многоугольника пересекается n/2

диагонали.

Введём функцию ${displaystyle delta _{m}(n)}$ , равную в случае, если делится на , и равную в противном случае. Тогда:

Количество точек пересечения диагоналей правильного -угольника равно

${displaystyle {begin{array}{l}C_{n}^{4}+left(-5n^{3}+45n^{2}-70n+24right)/24cdot delta _{2}(n)-(3n/2)cdot delta _{4}(n)+\+left(-45n^{2}+262nright)/6cdot delta _{6}(n)+42ncdot delta _{12}(n)+60ncdot delta _{18}(n)+\+35ncdot delta _{24}(n)-38ncdot delta _{30}(n)-82ncdot delta _{42}(n)-330ncdot delta _{60}(n)-\-144ncdot delta _{84}(n)-96ncdot delta _{90}(n)-144ncdot delta _{120}(n)-96ncdot delta _{210}(n)end{array}}}$

Где ${displaystyle C_{n}^{4}}$

– число сочетаний из

по

^[3].

Количество частей, на которые правильный -угольник делят его диагонали, равно

${displaystyle {begin{array}{l}left(n^{4}-6n^{3}+23n^{2}-42n+24right)/24+\+left(-5n^{3}+42n^{2}-40n-48right)/48cdot delta _{2}(n)-(3n/4)cdot delta _{4}(n)+\+left(-53n^{2}+310nright)/12cdot delta _{6}(n)+(49n/2)cdot delta _{12}(n)+32ncdot delta _{18}(n)+\+19ncdot delta _{24}(n)-36ncdot delta _{30}(n)-50ncdot delta _{42}(n)-190ncdot delta _{60}(n)-\-78ncdot delta _{84}(n)-48ncdot delta _{90}(n)-78ncdot delta _{120}(n)-48ncdot delta _{210}(n)end{array}}}$

^[3].

Применение[править | править код]

Правильными многоугольниками по определению являются грани правильных многогранников.

Древнегреческие математики (Антифонт, Брисон Гераклейский, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.^[4]

История[править | править код]

Построение циркулем и линейкой правильного многоугольника с сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на равных частей, так как, соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.

Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для . Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с $2^{m}$ сторонами (при целом m>1 ), имея уже построенный многоугольник с числом сторон ${displaystyle 2^{m-1}}$ : пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат, потом правильный восьмиугольник, правильный шестнадцатиугольник и так далее. Кроме этого, в той же книге Евклид указывает и второй критерий построимости: если известно, как строить многоугольники с и сторонами, и и взаимно простые, то можно построить и многоугольник с сторонами. Это достигается построением многоугольника с сторонами и многоугольника с сторонами так, чтобы они были вписаны в одну окружность и чтобы одна вершина у них была общей – в таком случае некоторые две вершины этих многоугольников будут являться соседними вершинами -угольника. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с ${displaystyle 2^{m}cdot 3}$ , ${displaystyle 2^{m}cdot 5}$ и ${displaystyle 2^{m}cdot 3cdot 5}$ сторонами при любом целом неотрицательном .

Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: . Вопрос о наличии или отсутствии других таких чисел остаётся открытым. Гаусс, в частности, первым смог доказать возможность построения правильного -угольника, а под конец жизни завещал выбить его на своём надгробии, однако скульптор отказался выполнять столь сложную работу.^[5]

Из результата Гаусса мгновенно следовало, что правильный многоугольник возможно построить, если число его сторон равно ${displaystyle 2^{k}{p_{1}}{p_{2}}cdots {p_{s}}}$ , где {k} — целое неотрицательное число, а ${p_{j}}$ — попарно различные простые числа Ферма. Гаусс подозревал, что это условие является не только достаточным, но и необходимым, но впервые это было доказано Пьером-Лораном Ванцелем в 1836 году. Итоговая теорема, совмещающая оба результата, называется Теоремой Гаусса-Ванцеля.

Последними результатами в области построения правильных многоугольников являются явные построения 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.

См. также[править | править код]

Правильный многогранник

Примечания[править | править код]

↑ МАТВОКС
↑ treugolniki.ru. Дата обращения: 12 мая 2020. Архивировано 2 июля 2020 года.
↑ ¹ ² ³ Bjorn Poonen and Michael Rubinstein “The number of intersection points made by thediagonals of a regular polygon”. Дата обращения: 16 июля 2020. Архивировано 17 июля 2020 года.
↑ А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5.
↑ Лабуда

Источник

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

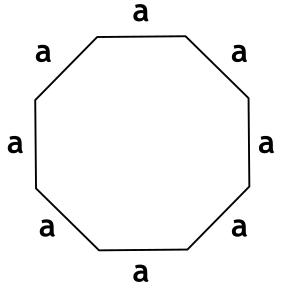
S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a – длина стороны многоугольника

n – число сторон многоугольника

Формула площади правильного многоугольника через радиус вписанной окружности

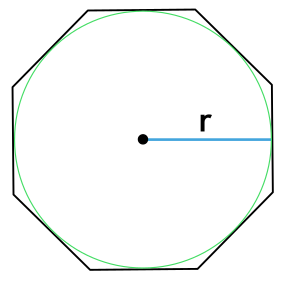
S = nr^2 tg dfrac{180°}{n}

r – радиус вписанной в многоугольник окружности

n – число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R – радиус описанной в многоугольник окружности

n – число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r – радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Площадь правильного многоугольника, формула

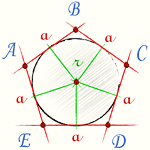
Для того чтобы вычислить площадь правильного многоугольника его разбивают на равные треугольники с общей вершиной в центре вписанной окружности. А площадь правильного многоугольника равна произведению его полупериметра на радиус вписанной окружности правильного многоугольника

[ S = r p = frac{1}{2} r n a ]

n — число сторон правильного многоугольника
p — полупериметр правильного многоугольника
a — сторона правильного многоугольника

r — радиус вписанной окружности правильного многоугольника

[ S = frac{n a^2}{4 tg(frac{360°}{2n})} ]

Вычислить, найти площадь правильного многоугольника по формуле (2)

Площадь правильного многоугольника	стр. 320

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Формулы площади правильного многоугольника

Площадь правильного многоугольника через радиус вписанной окружности

Связанные определения[править | править код]

Свойства[править | править код]

Координаты[править | править код]

Размеры[править | править код]

Площадь[править | править код]

Периметр[править | править код]

Свойства диагоналей правильных многоугольников[править | править код]

Применение[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

Содержание:

Формула площади правильного многоугольника через длину стороны и число сторон

Формула площади правильного многоугольника через радиус вписанной окружности

Формула площади правильного многоугольника через радиус описанной окружности

Пример задачи на нахождение площади правильного многоугольника

Площадь правильного многоугольника, формула

Вычислить, найти площадь правильного многоугольника по формуле (2)

Площадь правильного многоугольника

Вам также может понравиться

Как составить акт если не принимают претензию

Как найти географическое положение гор

Как правильно составить таблицу к тексту

Добавить комментарий Отменить ответ