Как найти площадь равностороннего треугольника по клеткам – Сайт, где вы сможете решить свои вопросы

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

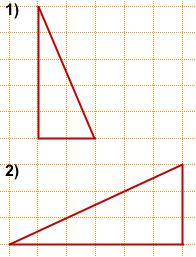На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

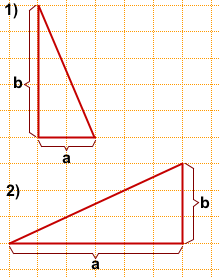ploshchad-pryamougolnogo-treugolnika-po-risunku 1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

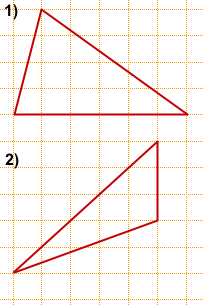На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

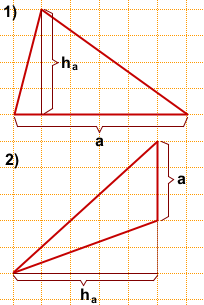ploshchad-treugolnika-na-kletchatoj-bumage a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

Задача 3

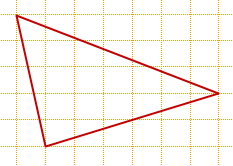
najti-ploshchad-treugolnika-po-risunku

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

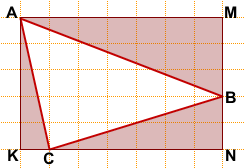
najti-ploshchad-treugolnika-na-bumage

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см

изображен треугольник (см. рис.). Найдите его площадь в квадратных

сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см

изображен треугольник (см. рис.). Найдите его площадь в квадратных

сантиметрах.

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см  times  1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

На клетчатой бумаге с клетками размером 1 см times 1 см изображена трапеция (см. рис.). Найдите ее площадь в квадратных сантиметрах.

На клетчатой бумаге с размером клетки дробь: числитель: 1, знаменатель: корень из: начало аргумента: Пи конец аргумента конец дроби см times дробь: числитель: 1, знаменатель: корень из: начало аргумента: Пи конец аргумента конец дроби см изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Площадь прямоугольного треугольника будем искать с помощью формулы

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

Иногда площадь треугольника можно найти как разность площадей других фигур.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

Площади прямоугольных треугольников найдём по формуле

Как найти треугольник по клеткам

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому

см 2 .

Приведём другое решение:

Воспользуемся формулой для нахождения площади треугольника

Одна из сторон данного треугольника является диагональю квадрата со стороной 6, а высота, проведённая к этой стороне, является диагональю квадрата со стороной 2. Тогда

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

[spoiler title=”источники:”]

http://ege.sdamgia.ru/search?search=%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D0%BF%D0%BB%D0%BE%D1%89%D0%B0%D0%B4%D1%8C%20%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BA%D0%BB%D0%B5%D1%82%D1%87%D0%B0%D1%82%D0%BE%D0%B9

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

[/spoiler]

Источник

Как найти площадь треугольника по клеткам?

2 ответа:

2

0

Будем предполагать, что все вершины треугольника находятся на пересечении линий сетки (в вершинах клеток. Проведите горизонтальные линии через “самую верхнюю” и “самую нижнюю” точки треугольника (это будут две из трех вершин). Аналогично, проведите вертикальные линии через “самую левую” и “самую правую” точки треугольника (это будут третья вершина и одна из первых двух вершин). Получился прямоугольник, в который “вписан” заданный треугольник. Заштрихуйте (закрасьте) его. Площадь прямоугольника и трех (в некоторых случаях, если одна из сторон треугольника лежит на одной из сторон прямоугольника, то двух) не закрашенных треугольников легко, а площадь заданного треугольника – это разность этих площадей.

2

0

Для решения таких задач существует теорема Пика.

Вы не уточнили, какой именно треугольник имеется в виду. Решения разнятся и дополнительные построения не для всех видов треугольников нужны. Поэтому посмотрите решения для всех видов.

Только учтите, что там в первой задаче опечатка: в произведении нет второго множителя -3.

И во второй тоже: в формуле ошибка.

Читайте также

Площадь любого треугольника равна 1/2 произведения основания на высоту. Пусть основание 8, а высота – x. Высота делит основание на 2 отрезка: y и (8 – y). Соответственно, образуются 2 прямоугольных треугольника со сторонами:

4, y, x и

6, (8 – y), x.

Для прямоугольных треугольников справедлива теорема Пифагора:

(1) 4^2 = x^2 + y^2 (значок “^” – возведение в степень),

(2) 6^2 = x^2 + (8 – y)^2 = x^2 + 8^2 – 2*8*y + y^2

Не мудрствуя лукаво, вычтем из уравнения (2) уравнение (1). Получаем:

36 – 16 = 64 – 16*y

откуда: y = 44/16 = 11/4 = 2,75

Из (1) определим x:

x = SQRT(16 – 2,75^2) = SQRT(8,4375) ~= 2,90473751

Откуда площадь: 1/2*8*x = 4*x ~= 11,61895004

<hr />

Тот же результат получается по формуле Герона:

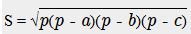
где p – полупериметр – (a + b + c)/2.

<hr />

Посчитать он-лайн площадь любого треугольника по 3-м сторонам можно тут или тут.

Вывод формулы Герона можно посмотреть тут или тут.

<hr />

P.S. Мне представляется, что для 4-го класса такие задачки решать рановато. Но измерять площадь любого треугольника уже можно с помощью палетки (сетки, накладываемой на фигуру)! Как определять площадь фигуры по формуле Пика (приблизительно) см. тут.

Первый вариант.

Можно использовать формулу Герона, которая позволяет вычислить площадь треугольника, если известны его стороны.

S=кв.корень[(p(p-a)(p-b)(p-c))], где p=(a+b+c)/2 – полупериметр треугольника со сторонами: a,b,c;

S – площадь треугольника.

Вычисляем:

p=(a+b+c)/2=(6+6+6)/2=9

S=к.кв[9(9-6)(9-6)(9-6)]=к.кв[9*3*3*3]=к.кв[243]=15,6 см кв.(приблизительно)

Второй вариант.

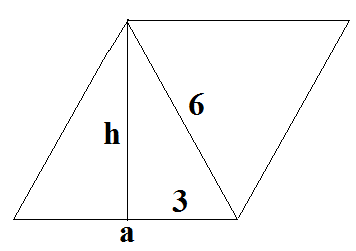
Имеем равносторонний треугольник со стороной a и высотой h, достраиваем его до параллелограмма.

Площадь параллелограмма=a*h, а площадь треугольника=a*h/2

Высота треугольника h по теореме Пифагора

h=кор.кв[a в кв.-(a/2)в кв.]=кор.кв[6 в кв.-3 в кв.]=кор. кв (36-9)=кор. кв 27=5,2 (приблизительно)

Тогда

Sтреугольника=a*h/2=6*5,2/2=15,6 приблизительно.

Самая простая задача.Равносторонний треугольник имеет стороны длиной в 1 метр.Найти периметр и площадь данного треугольника.Или другая простая задача.Найти периметр и площадь прямоугольного треугольника с катетами 3 и 4 метра.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки не лежащие на одной прямой. три точки – это вершины треугольника, три отрезка – стороны. Формул для вычисления площади существует много. Первая, которую изучают в школе – вычисление площади через основание и высоту S = 12ah.

Проще посмотреть здесь http://100formul.ru/55 – сайт дает возможность высчитать площадь онлайн. Кроме этого, формулы представлены на этом сайте http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA

Здесь можно посмотреть полную информацию, касающуюся треугольника.

С чертежом не могу, начертите сами.

Начертите прямоугольный треугольник с неравными катетами. Прямой угол обозначьте С. Катет Ас больше катета ВС. Впишите в треугольник окружность (центр О). Проведите радиусы к точкам касания, точки касания на катете АС обозначьте А1, на катете ВС – В1 на гипотенузе АВ обозначьте М.

Очевидно, что СА1ОВ1 – квадрат со стороной 2 см. ВМ и ВВ1 равны как касательные проведенные к окружности из одной точки. Аналогично АМ=АА1.

Тогда АВ=АМ+МВ=АА1+ВВ1=(АС-2)+(ВС-2)=(АС+ВС)-4=17-4=13 см.

Тогда периметр Р=17+13=30 см, полупериметр p=15 см, а площадь треугольника S=p*r=15*2=30 см^2.

Источник

Ира ЛДВО для БВ.

Для этого есть формула точек Пика.

Чем мельче сетка, тем больше точек и ответ более точен. В чём суть формулы Пика? Суть весьма проста. Надо расставить точки внутри любой фигуры, любой формы в перекрестьях клеток, затем расставить точки в самой линии периметра фигуры, также в перекрестьях клеток сетки. Вычислить все точки внутри прибавить половину количества точек периметра и отнять единицу от суммы.

В моём случае я их окрасила в 2 цвета внутренние точки синим, а внешние точки красным для удобства восприятия.

У меня вышло 18 синих и 3 красных. Беру формулу Пика и вычисляю:

S = В + Г/2 – 1. Вставляю значения чисел и вычисляю:

S = 18 + 3/2 – 1 = 18,5 кл^2.

Ира ЛДВО для БВ.

Проверка:

Я достроила до прямоугольника с площадью 10*5 = 50 кл^2.

Наименьшая сторона данного треугольника имеет диагональ в прямоугольнике 1*4 кл^2.

Средняя сторона данного треугольника имеет диагональ в прямоугольнике 1*9 кл^2. Но их по две, а диагональ делит прямоугольники надвое. Значит лишние как раз 2 прямоугольника. Их я и вычту из большого прямоугольника, и результат поделю пополам, чтобы узнать площадь данного треугольника. Вычисляю:

(50 – 4 – 9)/2 = 18,5 кл^2. Сходится с вычислениями по формуле Пика.

Проверка завершилась успешно!

Мой ответ: Площадь треугольника на клетчатой бумаге с размером клетки 1×1 равна 18,5 клеток.

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Как найти треугольник по клеткам

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Как найти площадь треугольника по клеткам?

Вам также может понравиться

Как найти иллюстраторов книги

Как составить организационный план предприятия

Как найти вес металла по размерам

Добавить комментарий Отменить ответ