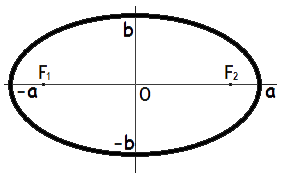Как найти площадь различными способами - Сайт, где вы сможете решить свои вопросы

Формулы площади геометрических фигур

Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p – a)(p – b)(p – c)
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,

p = a + b + c – полупериметр треугольника.

2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d₁, d₂ – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d₁, d₂ – длины диагоналей.

Формулы площади трапеции

Формула Герона для трапеции

S = a + b √(p-a)(p-b)(p-a-c)(p-a-d)

|a – b|
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,

p = a + b + c + d – полупериметр трапеции.

2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними

Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S – площадь четырехугольника,
d₁, d₂ – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r
Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p – a)(p – b)(p – c)(p – d) – abcd cos²θ

где S – площадь четырехугольника,

a, b, c, d – длины сторон четырехугольника,

p = a + b + c + d2 – полупериметр четырехугольника,

θ = α + β2 – полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность

S = √(p – a)(p – b)(p – c)(p – d)

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

S = π r²
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.

Формулы площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S – Площадь эллипса,

a – длина большей полуоси эллипса,

b – длина меньшей полуоси эллипса.

Источник

Содержание

Площадь фигур
Площадь квадрата
Площадь прямоугольника
Площадь сложных фигур
Различные способы вычисления площадей многоугольников
Скачать:
Предварительный просмотр:
Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью . Так при изучении темы «Площади многоугольников» встаёт вопрос: есть ли задачи, отличные от задач рассмотренных в учебнике геометрии. Есть ли другие способы вычисления площадей многоугольников? Можно ли вместо многочисленных формул для вычисления площадей различных многоугольников использовать одну универсальную формулу? Особенно остро этот вопрос встал в период подготовки к ОГЭ и ЕГЭ по математике. В контрольно- измерительных материалах ЕГЭ по математике присутствуют задания на вычисление площадей многоугольников. Мы провели опрос у старшеклассников, и из 25 учеников у 18 задание на нахождение площадей многоугольников вызывало затруднения, поэтому мы решили исследовать задачи на клетчатой бумаге, связанные с нахождением площади изображённой фигуры.

Площадь фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см 2

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

Площадь прямоугольника

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см 2

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м 2
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

АС — диагональ прямоугольника ABCD . Найдём площадь треугольников ABC и ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см 2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см 2

S_ABC = S_ACD = 10 см 2

Источник

Различные способы вычисления площадей многоугольников

Скачать:

Вложение	Размер
razlichnye_sposoby_vychisleniya_ploshchadey_mnogougolnikov_11i.zip	2.3 МБ

Предварительный просмотр:

Муниципальное автономное образовательное учреждение

«Средняя общеобразовательная школа № 7»

Научно-практическая конференция «Шаг в будущее»

«РАЗЛИЧНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ

Авторы : ученики 11 «И» класса

Дубица Ольга Сергеевна

Кондрашкина Алина Андреевна

Руководитель : учитель математики

Новолодская Лариса Владимировна

Великие математики о вычислении площадей ………………………….6

Георг Пик и его теорема ……………………………………………………7

Способы вычисления площадей многоугольников …………………….8

Первое условие, которое надлежит выполнять в математике, —

это быть точным, второе –

быть ясным и, насколько можно, простым.
Лазар Карно

Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью . Так при изучении темы «Площади многоугольников» встаёт вопрос: есть ли задачи, отличные от задач рассмотренных в учебнике геометрии. Есть ли другие способы вычисления площадей многоугольников? Можно ли вместо многочисленных формул для вычисления площадей различных многоугольников использовать одну универсальную формулу? Особенно остро этот вопрос встал в период подготовки к ОГЭ и ЕГЭ по математике. В контрольно- измерительных материалах ЕГЭ по математике присутствуют задания на вычисление площадей многоугольников. Мы провели опрос у старшеклассников, и из 25 учеников у 18 задание на нахождение площадей многоугольников вызывало затруднения, поэтому мы решили исследовать задачи на клетчатой бумаге, связанные с нахождением площади изображённой фигуры.

Мы изучили литературу, Интернет-ресурсы по данной теме. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Не судите поспешно. Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Мы научились вычислять площади многоугольников, нарисованных на клетчатом листке.

Объект исследования : задачи на клетчатой бумаге.

Предмет исследования : задачи на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Методы исследования : моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.

Цель исследования : Вывести и проверить формулы вычисления площадей геометрических фигур с помощью формулы Пика.

Для достижения поставленной цели необходимо решение следующих задач :

Изучить литературу по исследуемой теме.
Отобрать материал для исследования, выбрать главную, интересную, понятную информацию.
Проанализировать и систематизировать полученную информацию
Расширить кругозор, изучив дополнительный материал по истории вычисления площадей.
Создать электронную презентацию работы для представления собранного материала.

Гипотеза : Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле планиметрии.

Актуальность : Задачи на нахождение площадей решетчатых многоугольников часто встречаются на ЕГЭ по математике.

В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычислять их площади. По-видимому, в древности приходилось рассматривать лишь участки, мало отличающиеся от прямоугольника по форме, а для таких участков погрешность невелика. Лишь в последствие было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника, трапеции и других многоугольников. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников.

Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий. Еще 4 — 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служит эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, ими можно заполнить плоскость без пробелов.

В древнем Китае мерой площади был прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалась на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту и т.п. Для вычисления площади четырехугольника умножались полусуммы противоположных сторон.

ВЕЛИКИЕ МАТЕМАТИКИ О ВЫЧИСЛЕНИИ ПЛОЩАДЕЙ

Тема нахождения площадей многоугольников всегда волновала умы многих великих математиков. В своих «Началах» Евклид не употреблял слова «площадь», так как он под самим словом «фигура» понимал часть плоскости, ограниченную той или иной замкнутой линией. Евклид сравнивал площади разных фигур между собой. Как и другие ученые древности, Евклид занимался вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур.

Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. Имя Герона навсегда связано с известной формулой нахождения площади треугольника, если даны три его стороны a, b, c:

Великому Архимеду принадлежат формулировки многих теорем о площадях и объемах сложных фигур и тел, вполне строго доказанные им методом исчерпывания.

Гиппократ Хиосский, живший во второй половине V века до н. э исследовал площади плоских фигур, ограниченных как прямыми линиями, так и дугами окружности. Не остался в стороне и всем известный Пифагор. С помощью его знаменитой теоремы доказаны и выведены многие формулы для вычисления некоторых многоугольников.

ГЕОРГ ПИК И ЕГО ТЕОРЕМА

Настоящая жемчужина нашего исследования задач на нахождение площадей – это формула Пика. Сто лет назад немецкий математик Георг Пик открыл и доказал замечательную формулу для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги. У формулы Пика есть связь со знаменитой формулой Эйлера, связывающей количества вершин, рёбер и граней выпуклого многогранника.

Георг Алекса́ндр Пик ( 10 августа 1859 — 13 июля 1942 ) — австрийский математик , родился в еврейской семье (Приложение 1).

Круг математических интересов Пика был чрезвычайно широк. Им написаны работы в области математического анализа, дифференциальной геометрии, в теории дифференциальных уравнений и т. д., всего более 50 тем. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.

Для начала рассмотрим, как можно вычислить площадь прямоугольника, применив теорему Пика.

Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки ( Приложение 2). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
S = В + + 4 · = В + — 1 .

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + — 1 . Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ.

Мы провели исследование с целью выявления и сравнения различных способов вычисления многоугольников.

Сюжет будет разворачиваться на обычном листке клетчатой бумаги (Приложение 3) . Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить. Но тут нас ждёт много хлопот (попробуйте!).

Давайте «схитрим»: вычислим площадь заштрихованной фигуры, которая «дополняет» наш многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.

Если даны более простые многоугольники, например, треугольник, параллелограмм или трапеция, то достаточно применить известные в общеобразовательной программе формулы для вычисления площадей.

Итак, рассмотрим способы вычисления площади на самом простом примере многоугольника: на треугольнике (Приложение 4) .

Задача : на клетчатой бумаге 1 см × 1 см изображён треугольник. Найти его площадь.

1 способ . «Считаем по клеточкам» (Приложение 5) .

1.Посчитаем количество полных клеток внутри данного треугольника. (10 )

2.Дополним неполные клетки друг другом до полных клеток. (5 )

3. Сложим полученные количества полных клеток: ( 10+5 = 15 )

2 способ . «Формула площади фигуры» (Приложение 6).

1.Площадь искомого треугольника найдем по формуле:

S тр =(а•h)/2, где а – основание треугольника, h – его высота, проведенная к этому основанию. а=6, h=5

3 способ . «Сложение площадей фигур» (Приложение 7).

1.Разобьем данный треугольник на два прямоугольных треугольника, для этого проведем высоту.

2.Найдем площадь прямоугольного треугольника S 1 : S 1 = (5Х5)/2=12,5

3.Найдем площадь прямоугольного треугольника S 2 : S 2 = (5х1)/2=2,5

4.Площадь искомого треугольника найдем по формуле:

4 способ . «Вычитание площадей фигур» (Приложение 8).

1.Достроим до прямоугольника со сторонами 5 и 6.

2.Найдем площадь прямоугольника: S пр =5Х6=30

3.Найдем площадь прямоугольного треугольника S 1 : S 1 = (5Х5)/2=12,5

4.Найдем площадь прямоугольного треугольника S 2 : S 2 = (5х1)/2=2,5

5.Площадь искомого треугольника найдем по формуле:

S тр =S пр -(S1+S2) S тр =30-(12,5+2,5)= 15

Но если треугольник будет иметь другое расположение, то основание и высоту в таком треугольнике определить точно невозможно, а, следовательно, невозможно применить формулу для вычисления его площади (Приложение 9).

Поэтому здесь можно только применить способ вычитания прямоугольных треугольников из площади прямоугольника.

S прямоугольника = 6*5 = 30 см 2 , S 1 = ½ *5*2 = 5 см 2 , S 2 = ½ *4*2=4 см 2 ., S 3 =½*6*3 = 9 см 2 Тогда S треугольника = S прямоугольника — S 1 — S 2 — S 3 = 30 – 5 – 4 – 9 = 12 см 2

Все другие способы, рассмотренные здесь тоже достаточно трудоёмки.

Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади нам пришлось потрудиться. И вот тут на первый план выходит ещё один способ.

5 способ . «Формула Пика» (Приложение 10).

Площадь искомого треугольника найдем по формуле Пика: S=Г/2+В-1,

где Г –количество узлов на границе треугольника(на сторонах и вершинах),

В – количество узлов внутри треугольника. Г = 12, В = 10,

Как видите, формула Пика очень удобна и проста в применении.

А теперь давайте попробуем вычислить площадь этого треугольника с помощью формулы Пика (Приложение 11).

S = 10 + 6/2 – 1 = 12. Оказывается, это намного быстрее, чем в предыдущем случае!
А если бы многоугольник выглядел более причудливо?

Можно убедиться в том, что формула Пика верна для всех рассмотренных примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика (Приложение 12).

Рассмотрим ещё некоторые задачи на клетчатой бумаге с клетками размером 1 см 1 см

Задача 1. Найдите площадь прямоугольника АВСD (Приложение 13).
Решение. По формуле Пика: S = В + — 1 .

В = 8, Г = 6
S = 8 + 6/2 – 1 = 10 (см²)
Ответ: 10 см².

Задача 2. Найдите площадь параллелограмма АВСD (Приложение 14).
Решение. По формуле Пика: S = В + — 1 .

S = 6 + 6/2 – 1 = 8 (см²)
Ответ: 8 см².

Задача 3 . Найдите площадь треугольника АВС (Приложение 15).
Решение. По формуле Пика: S = В + — 1 .

S = 6 + 5/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².

Задача 4. Найдите площадь четырёхугольника АВСD (Приложение 16).

Решение. По формуле Пика: S = В + — 1 .

S = 5 + 7/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².

Согласитесь, рассмотренные задания аналогичны заданию В3 из вариантов контрольно-измерительных материалов ЕГЭ по математике. Теперь, зная формулу Пика, мы можем вычислить площадь любого многоугольника, даже самой причудливой формы, если он изображён на клетчатой бумаге.

Мы изучили литературу по исследуемой теме, проанализировали и систематизировали полученную информацию, познакомились со способами вычисления площадей многоугольников, в том числе с помощью формулы Пика.

Задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач. Задача на нахождение площади многоугольника с вершинами в узлах сетки сподвигла австрийского математика Пика в 1899 году доказать замечательную формулу Пика.

В ходе своей исследовательской работы мы нашли и изучили различные способы вычисления площадей многоугольников на клетчатой бумаге, сопоставила их. Любой из этих способов применим для решения задач типа В3 ЕГЭ по математике. Но наиболее удобен, на наш взгляд, способ «Формула Пика», который имеет перед другими способами ряд преимуществ:

Для вычисления площади многоугольника, нужно знать всего одну формулу: S = В + — 1 .
Формула Пика очень проста для запоминания.
Формула Пика очень удобна и проста в применении.
Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.

Даже великие ученые говорили, что геометрия является могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать .
ЛИТЕРАТУРА

2. Григорьева Г. И . Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009.

3. Жарковская Н. М., Рисс Е. А . Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.

4. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа: http://mathege.ru/or/ege/ShowProblems.html?posMask=32

5. Игнатьев Е. И . В царстве смекалки. – М.: Наука, 1982.

6. Прасолов В. В . Задачи по планиметрии. – М.: МЦНМО, 2000.

7. Смирнова И. М., Смирнов В. А . Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.

8. Смирнова И. М., Смирнов В. А . Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.

9. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008.

10. Гарднер М. Математические чудеса и тайны. – М.: Наука

Источник

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см²

S_ABC =
S_ACD = 10 см²

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

3 декабря 2015 в 22:54

Ирина Петренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ирина Петренко
Профиль
Благодарили: 0

Сообщений: 1

как написать правильно площадь треугольника?

0
Спасибо thanks
Ответить

9 декабря 2015 в 19:41
Ответ для Ирина Петренко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8

S(рисуешь мини треугольник) = ,,,,,

0
Спасибо thanks
Ответить

Источник

Разные способы вычисления площадей фигур

Авторы
Руководители
Файлы работы
Наградные документы

Боташева С.М. 1

1Дворец творчества детей и молодежи, г. Нальчик

Суншева З.Н. 1

1Дворец творчества детей и молодежи, г.Нальчик

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Математика – один из моих любимых школьных предметов. А самое сложное и одновременно самое интересное в математике – решение задач. Задачи в учебнике и сборниках попадаются самые разные и способов решения каждой задачи можно придумать несколько. Но один вид задач, как мне кажется, не похож на другие. Это задачи на клетчатой бумаге. Они кажутся необычными, более занимательными.

А встречаются ли такие задачи старшеклассникам? Я решила посмотреть открытый банк заданий ОГЭ и ЕГЭ по математике, посетить сайты по подготовке выпускников 9 и 11 классов к экзаменам. Оказалось, что задачи на нахождение площадей многоугольников на клетчатой бумаге достаются на экзаменах почти каждому выпускнику.

Вывод прост: уметь решать задачи на сетке (в т.ч. на нахождение площадей) разными способами нужно уметь каждому школьнику. В этом я вижу актуальность моей работы, а ее новизну в том, что один из рассматриваемых способов решения не разбирается в школьных учебниках математики.

Цель исследования – изучить способы вычисления площадей фигур на клетчатой бумаге, и выбрать самый эффективный.

Для достижения данной цели необходимо выполнить следующие задачи:

Подобрать литературу по данной теме.
Изучить способы нахождения площадей фигур на клетчатой бумаге.
Провести эксперимент.
Сделать выводы.

Предмет исследования: площади фигур на клетчатой бумаге.

Объект исследования: фигуры на клетчатой бумаге.

Гипотеза: самым эффективным способом вычисления площадей фигур на клетчатой бумаге является – формула Пика.

Глава 1. Способы нахождения площадей фигур на клетчатой бумаге. 1.1Площадь фигуры как сумма площадей ее частей

Задача №1. Найти площадь фигуры на рисунке 1 (клетки размером 1х1 см).

Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.

S=S1+ S2+ S3+S4

S1=2*3= 6 см2; S2= *2*1=1 см2;

S3= *2*1= 1 см2; S4= *3*1= 1,5 см2

S= 6+1+1+1,5= 9,5 см2.

Рис. 1. Ответ: 9,5 см2

Задача №2. Найти площадь фигуры на рисунке 2 (клетки размером 1х1 см).

S=S1+ S2+ S3+S4

S1= *1*5= 2,5 см2; S2=4*2=8 см2;

S3= *1*2= 1 см2; S4= *2*4= 4 см2;

S= 2,5+8+1+4= 15,5 см2.

Ответ: 15,5 см2.

Рис. 2.

Задача №3. Найти площадь фигуры на рисунке 3 (клетки размером 1х1 см).

Разбиваем данную фигуру на три части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.

S=S1+ S2+ S3

S1= *2*5= 5 см2;

S2=5*5=25 см2;

S3= *2*5= 5 см2;

S= 5+25+5= 35 см2

Рис. 3. Ответ: 35 см2.

1.2. Площадь фигуры как часть площади прямоугольника

Задача № 4. Найти площадь фигуры на рисунке 4 (клетки размером 1х1 см).

Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:

S=Sпр – S1 – S2 – S3

Sпр=5*5=25 см2; S1= *5*4=10 см2;

S2= *5*2=5 см2; S3= *1*3=1,5 см2;

S=25-10-5-1,5=8,5 см2

Ответ: 8,5 см2.

Рис.4.

Задача №.5. Найти площадь фигуры на рисунке 5 (клетки размером 1х1см).

S=Sпр – S1 – S2 – S3 – S4

Sпр=7*7= 49 см2; S1= *2*5=5 см2;

S2= *2*5=5 см2; S3= *2*5=5 см2;

S4= *2*5=5 см2;

S= 49-5-5-5-5= 29 см2

Ответ: 29 см2.

Рис.5.

Задача №.6. Найти площадь фигуры на рисунке 6 (клетки размером 1х1см).

S=Sпр – S1 – S2

Sпр=5*5=25 см2;

S1= *3*1=1,5 см2; S2= *4*5=10 см2;

S= 25-1,5-10=13,5 см2.

Ответ: 13,5 см2.

Рис. 6.

1.3. Формула Пика

Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье. Его отец Адольф Йозеф Пик возглавлял частный институт. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

В 1900 – 1901 годах занимал пост декана философского факультета.

После того как Пик вышел в отставку в 1927 году, он получил звание почётного профессора и вернулся в Вену – город, в котором он родился. Однако в 1938 году после аншлюса Австрии 12 марта он вернулся в Прагу. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Круг математических интересов Георга Пика был чрезвычайно широк: 67 его работ посвящены многим темам, таким как линейная алгебра, интегральное исчисление, функциональный анализ, геометрия и др. Но больше всего он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года.

Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 году польский математик Гуго Штейнгауз включил теорему (или как её ещё называют – формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники.

Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, S – его площадь. Тогда справедлива следующая формула:

S = В+ – 1 ,

Это и есть формула Пика.

Задача №7. Вычислить площадь многоугольника на рисунке 7. Воспользуемся формулой Пика.

Отметим узлы:

Г=9 (синие)

В=48 (красные)

Подставив в формулы наши данные, получаем:

Рис.7. S=48 + – 1 = 51,5 см2 .

Задача №8. Вычислить площадь многоугольника на рисунке 8. Воспользуемся формулой Пика.

Отметим узлы:

Г=9 (синие)

В=16 (красные)

Подставив в формулы наши данные, получаем:

S=16 + – 1 = 19,5 см2 .

Рис. 8.

Задача № 9. Вычислить площадь многоугольника на рисунке 9. Воспользуемся формулой Пика.

Отметим узлы:

Г=8 (синие)

В=24 (красные)

Подставив в формулы наши данные, получаем

S=24 + – 1 = 19 см2 .

Рис. 9.

Глава 2. Проведение эксперимента

2.1. Результаты эксперимента

Изучив все способы нахождения площадей фигуры на клетчатой бумаге, мы решили провести эксперимент. Исследование проводилось в объединении «Знаю и считаю» Дворца творчества детей и молодежи, в котором я обучаюсь. Вместе с нашим педагогом, который также является моим научным руководителем, мы объяснили ребятам все способы вычисления площадей фигур. Затем, мы им раздали задания: по три задачи по каждому способу, и предложили решить их на время. Мы с моим научным руководителем засекали время, а ребята решали задачи.

В Таблице 1 представлены результаты каждого обучающегося по трем способам:

№	Ф.И. учащихся	Время, затраченное на решение задач 1-м методом (мин)	Время, затраченное на решение задач 2-м методом (мин)	Время, затраченное на решение задач 3-м методом (Формула Пика) (мин)
1	Алина	3,23	4,33	1,04
2	Дана	4,12	4,54	1,43
3	Дарина	5,07	4,46	2,15
4	Алина	2,32	2,45	1,12
5	Инал	2,17	2,34	0,52
6	Лалина	5,43	6,31	3,23
7	Залина	4,43	4,23	2,38
8	Руслан	2,34	3,43	1,15
9	Алина	3,56	4,52	2,43
10	Даяна	3,15	3,49	1,34
11	Алихан	2,24	2,15	0,54
12	Милена	3,12	4,37	1,32
13	Артур	5,34	5,12	2,33
14	Александр	4,47	5,42	2,46
15	Ислам	5,36	6,13	3,52
	Всего:	3,43	4,22	1,07

Как видно из таблицы, меньше всего времени ребята затратили, решая задачи формулой Пика. В среднем на три задачи ребята потратили 1 минуту, 7 секунд – формулой Пика, а на задача другими способами – 3 минуты 43 секунды и 4 минуты 22 секунды. Но быстро не всегда означает правильно, поэтому мы посчитали количество допущенных ошибок каждого обучающегося по всем способам. Результаты представлены в Таблице 2:

№	Ф.И. учащихся	Количество допущенных ошибок в задачах, решенных 1 методом	Количество допущенных ошибок в задачах, решенных 2 методом	Количество допущенных ошибок в задачах, решенных 3 методом
1	Алина	1	2	0
2	Дана	2	1	1
3	Дарина	2	3	2
4	Алина	0	0	0
5	Инал	0	0	0
6	Лалина	3	3	2
7	Залина	1	2	1
8	Руслан	1	1	0
9	Алина	2	2	1
10	Даяна	1	2	0
11	Алихан	0	0	0
12	Милена	1	1	0
13	Артур	2	3	2
14	Александр	2	2	1
15	Ислам	3	3	1
	Всего ошибок из 45 задач:	21	25	11

Из таблицы видно, что меньше всего ошибок ребята сделали, решая задачи формулой Пика. По первому методу 21неправильных задач из 45, по второму методу 25 неправильных, а по третьему методу всего 11 неправильных задач из 45, причем 7 учеников из 15 сделали все три задачи правильно, пользуясь этим методом. Это означает, что формула Пика не только сокращает время, но и помогает избежать ошибок.

Заключение

В данной работе мы рассмотрели все способы вычисления площадей фигур на клетчатой бумаге. В ходе исследования, наша гипотеза подтвердилась. В результате эксперимента, мы выяснили, что формула Пика является самым эффективным способом решения таких задач. Она проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника. Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

Я уверена, что при сдаче выпускных экзаменов, задачи на вычисление площади фигур не будут вызывать затруднения, если ребята будут использовать формулу Пика.

Список использованной литературы

Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009
Математика? Легко!!! Площади фигур. – [Электронный ресурс].
Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс].

Приложения

Приложение 1

Площадь фигуры равна сумме площадей ее частей.

Площадь фигуры как части площади прямоугольника.

Формулу Пика.

Просмотров работы: 910

Источник

1. Формула площади равнобедренной трапеции через стороны и угол