Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
Основание треугольника:
a =
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
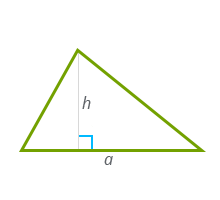
1) через основание и высоту
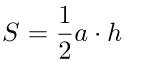
a – основание треугольника,
h – высота треугольника.
2) через две стороны и угол
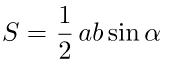
a, b – стороны треугольника,
α – угол между сторонами.
3) По трем сторонам. Формула Герона.
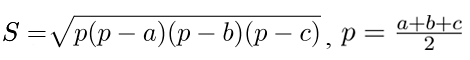
a, b, с – стороны треугольника,
p – полупериметр треугольника.
4) Через радиус вписанной окружности.
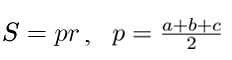
a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
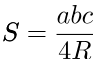
a, b, с – стороны треугольника,
R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Вы здесь
Калькулятор площади треугольника
Версия для печати
Существует множество способов вычисления площади треугольника: по высоте и основанию, по двум сторонам и углу между ними, по трём сторонам. В последнем случае используется, знакомая всем со школы, формула Герона. Данный метод уникален тем, что помогает произвести вычисления вне зависимости от типа фигуры. Если известно, что треугольник прямоугольный, равнобедренный или равносторонний, то для расчётов может понадобиться меньшее количество исходных данных. Площадь треугольника, построенного на векторах, вычисляется через векторное произведение этих величин. Фигура, вершины которой заданы через координаты в пространстве, рассчитывается путём нахождения расстояний между точками, а затем подстановки полученных значений в уже упомянутую формулу Герона. Онлайн-калькулятор позволит найти площадь треугольника удобным для пользователя способом в зависимости от начальных значений.
Калькулятор площади треугольника
Выберите тип треугольника:
Выберите способ расчета площади треугольника:
Округлять результат до знаков после запятой
Как рассчитать площадь
- Сначала необходимо выбрать тип фигуры. Треугольник может быть разносторонним, равнобедренным, прямоугольным или равносторонним. Если тип неизвестен, то оставляйте первый вариант.
- Далее в зависимости от исходных данных требуется выбрать способ расчёта.
- После этого нужно ввести начальные значения и определиться с количеством знаков после запятой.
- Вычисления производятся по нажатию кнопки “Рассчитать”.
Формулы расчёта площади треугольника
Разносторонний треугольник
- По трём сторонам
S = √(p·(p – a)·(p – b)·(p – c)), P = (a+b+c)/2 – формула Герона,
где a, b, c – стороны треугольника, p – полупериметр. - По двум сторонам и углу между ними
S = 0,5·a·b·sin α,
где a и b – стороны, α – угол между ними. - По стороне и двум прилежащим углам
S = a²·sin α·sin β/2sin(α + β),
где а – сторона, α и β – прилежащие углы. - По высоте и основанию
S = 0,5·a ·h,
где a – сторона, h – опущенная на неё высота. - По координатам вершин
Вычисление длин сторон:
АB = √((x1 – x2)² + (y1 – y2)² + (z1 – z2)²);
BC = √((x2 – x3)² + (y2 – y3)² + (z2 – z3)²);
CA = √((x3 – x1)² + (y3 – y1)² + (z3 – z1)²);
После этого необходимо подставить полученные значения в формулу Герона. - По координатам векторов
S = 0,5·|a × b| – половина модуля векторного произведения векторов.
Равнобедренный треугольник
- По стороне и основанию
S = (а/4)·√(4·b² – a²),
где a – основание, b – сторона. - По высоте и основанию
S = 0,5·a·h,
где a – основание, h – опущенная на неё высота. - По равным сторонам и углу между ними
S = 0,5·b²·sin α,
где b – сторона, α – угол между равными сторонами - По основанию и прилежащему углу
S = tg α·a²/4,
где a – основание, α – угол при основании.
Прямоугольный треугольник
- По двум катетам
S = 0,5·a·b,
где а – первый катет, b – второй катет. - По гипотенузе и высоте
S = 0,5·с·h,
где c – гипотенуза, h – опущенная на неё высота. - По катету и гипотенузу
S = 0,5·а·√(c² – a²),
где а – катет, c – гипотенуза. - По гипотенузе и прилежащему углу
S = с²·sin 2α/4,
где с – гипотенуза, α – прилежащий угол. - По катету и прилежащему углу
S = 0,5·a²·tg α,
где а – катет, α – прилежащий угол.
Равносторонний треугольник
- По стороне
S = √3·a/4,
где а – сторона правильного треугольника. - По высоте
S = h²/√3,
где h – высота правильного треугольника, проведённая на любую из сторон.

Формула:
S
=
1
2
ab
·
sin(α)
Где: a, b – катеты, c – гипотенуза.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
4R
Где: a, b, c – стороны разностороннего треугольника, R – радиус описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
2D
Где: a, b, c – стороны разностороннего треугольника, D – диаметр описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Формула:
S
=
a
b
c
4
S
π
Где: a, b, c – стороны разностороннего треугольника, S – площадь описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
π
a
b
c
2P
Где: a, b, c – стороны разностороннего треугольника, P – длина описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
R
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, R – радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
D
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, D – диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
SO
π
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, SO – площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
P
π
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, P – длина вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
a2
2
·
sin(α)
·
sin(β)
sin(180-(α+β))
Где: a – сторона, α, β – прилегающие углы.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
p(p-a)(p-b)(p-c)
p
=
a
+
b
+
c
2
Где: a, b, c – стороны, p – половина периметра.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна квадратному корню из произведения полупериметра, разницы полупериметра и стороны a, разницы полупериметра и стороны b, разницы полупериметра и стороны c. Полупериметр это сумма длин всех сторон треугольника разделенная на 2.
Калькуляторы площади разностороннего треугольника
Площадь треугольника разностороннего через две стороны и угол между ними

Где: a, b – катеты, c – гипотенуза.
вычислить
Площадь треугольника разностороннего через радиус описанной окружности и три стороны

Где: a, b, c – стороны разностороннего треугольника, R – радиус описанной окружности.
вычислить
Площадь треугольника разностороннего через диаметр описанной окружности и три стороны

Где: a, b, c – стороны разностороннего треугольника, D – диаметр описанной окружности.
вычислить
Площадь треугольника разностороннего через площадь описанного круга и три стороны
Где: a, b, c – стороны разностороннего треугольника, S – площадь описанной окружности.
вычислить
Площадь треугольника разностороннего через длину описанной окружности(периметр) и три стороны

Где: a, b, c – стороны разностороннего треугольника, P – длина описанной окружности.
вычислить
Площадь треугольника разностороннего через радиус вписанной окружности и три стороны

Где: a, b, c – стороны разностороннего треугольника, R – радиус вписанной окружности.
вычислить
Площадь треугольника разностороннего через диаметр вписанной окружности и три стороны

Где: a, b, c – стороны разностороннего треугольника, D – диаметр вписанной окружности.
вычислить
Площадь треугольника разностороннего через площадь вписанного круга и три стороны

Где: a, b, c – стороны разностороннего треугольника, SO – площадь вписанной окружности.
вычислить
Площадь треугольника разностороннего через длину (периметр) вписанной окружности и три стороны

Где: a, b, c – стороны разностороннего треугольника, P – длина вписанной окружности.
вычислить
Площадь треугольника разностороннего через сторону и два прилегающих угла

S
=
a2
2
·
sin(α)
·
sin(β)
sin(180-(α+β))
Где: a – сторона, α, β – прилегающие углы.
вычислить
Площадь разностороннего треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Разносторонним называется треугольник, у которого все три стороны не равны.

Формула площади треугольника:  ,
,
где a – сторона треугольника, h – высота
Используя этот онлайн калькулятор, вы сможете найти площадь разностороннего треугольника.
Поделиться страницей в социальных сетях:
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.
